II. SE�ALES, SISTEMAS Y SUS CARACTER�STICAS
DEBIDO A LA GRAN IMPORTANCIA que en el contexto de la informaci�n
y las telecomunicaciones, tienen las se�ales y los sistemas, el prop�sito de
este cap�tulo consiste en presentar las ideas y los conceptos necesarios para
que se entienda lo que es una se�al y un sistema, as� como la manera en que
interact�an en las telecomunicaciones. No es �nicamente en dicha �rea donde
han adquirido importancia; tambi�n en otros campos del conocimiento, tales como
aeron�utica, astron�utica, ac�stica, sismolog�a, ingenier�a biom�dica, medicina
en general (recu�rdese la importancia que tienen los electrocardiogramas y los
electroencefalogramas, as� como las tomograf�as axiales computarizadas y los
estudios basados en resonancia magn�tica nuclear), sistemas de generaci�n y
distribuci�n de energ�a el�ctrica, control de procesos de transformaci�n (ingenier�a
qu�mica) y de manufactura (ingenier�a industrial o mec�nica), uso dom�stico
y entretenimiento (vale la pena resaltar el efecto que recientemente han tenido
los discos compactos, conocidos com�nmente como CD, en los cuales,
a pesar de tratarse de se�ales ac�sticas de alta fidelidad, es decir, m�sica,
cada una de sus componentes genera y procesa alg�n tipo de informaci�n; este
ejemplo ser� analizado m�s adelante).
En cada una de esas �reas del conocimiento, las se�ales utilizadas son de distinta naturaleza: en ac�stica se trata de se�ales generadas por fuentes de sonido como la voz, la m�sica o cualquier clase de ruido; en control de procesos pueden ser se�ales de tipo t�rmico, mec�nico o el�ctrico generadas por los procesos mismos; en medicina pueden ser se�ales el�ctricas o magn�ticas generadas por el organismo humano; en sismolog�a se trata de se�ales mec�nicas, es decir, movimientos de la corteza terrestre. Sin embargo, todas ellas tienen algo en com�n: cada se�al tiene una o m�s caracter�sticas que reflejan el comportamiento de uno o varios fen�menos f�sicos; es decir, que en alguna de sus caracter�sticas contiene informaci�n acerca de los fen�menos f�sicos que entran en juego.
Para analizar esto con mayor detalle, consid�rese como ejemplo el �rea de la sismolog�a. El fen�meno f�sico participante en la generaci�n de un sismo es el movimiento brusco de las capas que forman la corteza terrestre. Como estos movimientos generalmente son de tipo "impulsivo", producen, a su vez, movimientos en la superficie terrestre, ocasionando lo que se conoce como un sismo. Dicho movimiento tiene ciertas caracter�sticas, tales como intensidad y naturaleza ondulatoria. Si el movimiento de la superficie terrestre se traduce de alguna manera a una se�al el�ctrica, las caracter�sticas de la se�al s�smica se preservan, pero en este caso se contar�a con una se�al que podr�a ser estudiada con mayor facilidad que la se�al mec�nica original. Considerando que un posible futuro gran sismo que afectar�a de manera muy negativa a la ciudad de M�xico podr�a generarse en la costa del estado de Guerrero, recientemente se instal� en esa zona un conjunto de sensores (sistemas que detectan los movimientos de las capas terrestres con base en aceleraciones) que generan se�ales el�ctricas caracter�sticas de los movimientos de tipo mec�nico por lo com�n asociadas a los sismos. Estas se�ales son transmitidas v�a radio a la ciudad de M�xico. Como los movimientos generados por el sismo viajan a lo largo de la superficie terrestre a una velocidad de aproximadamente 300 metros por segundo, y las se�ales de radio viajan a la velocidad de la luz, las se�ales el�ctricas transmitidas por este medio son recibidas en M�xico antes de la llegada de las ondas s�smicas (es decir, del temblor). Con ello, los habitantes de la ciudad de M�xico dispondr�n de un tiempo valios�simo antes de la llegada del sismo, durante el cual, si la poblaci�n est� bien capacitada y entrenada, se pueden realizar labores de evacuaci�n.
En este ejemplo se aprecia la dependencia que existe entre el tiempo y una se�al: cualquier persona que haya estado presente durante un sismo, recordar� que conforme avanza el tiempo los movimientos de la tierra cambian de sentido, se percibe una especie de "vaiv�n" o de "sube y baja", y, afortunadamente, tambi�n conforme avanza el tiempo, la intensidad de los movimientos disminuye hasta que todo vuelve a su estado inicial de reposo.
Esta dependencia del tiempo es una de las caracter�sticas m�s importantes de casi todas las se�ales que ser�n tratadas en este libro. En t�rminos un poco m�s formales, las caracter�sticas de la se�al son "una funci�n del tiempo". Para ilustrar esto, en la figura II.1 se presentan dos se�ales aparentemente iguales en forma, pero distintas entre s� porque su relaci�n con el tiempo es diferente: la primera tiene una duraci�n de 5 segundos, elev�ndose a su valor m�ximo en 3 segundos, mientras que la segunda sube a su valor m�ximo en 2 segundos y tiene una duraci�n total de 11/3 segundos.
En lo sucesivo, para indicar de manera expl�cita que la se�al es funci�n del tiempo, se utilizar� la siguiente notaci�n:
y, x, u otra letra indica la amplitud de la se�al;
y(t) o x(t) indica que y o x son funci�n del tiempo.
Figura II.1 Dos se�ales con igual forma pero distinta relaci�n temporal.
En los ejemplos mencionados, las se�ales var�an de una manera continua en funci�n del tiempo; esto significa que conforme avanza el tiempo la se�al adquiere valores dentro de un intervalo continuo. Ello se puede aclarar si se analiza un ejemplo donde esto no ocurra. Consid�rese una se�al proveniente de un contador de veh�culos al pasar por una caseta de peaje en una carretera. En este caso, el valor que adquiere la se�al de conteo puede ser uno de los n�meros asociados con un proceso de conteo: a lo largo del tiempo pueden haber pasado por la caseta 1, 82 ó 197 veh�culos, pero el n�mero de veh�culos no puede haber sido 63.3. A diferencia del primer caso, en que se habla de "se�ales continuas en amplitud" o "se�ales anal�gicas", esta segunda clase de se�ales se denomina "se�ales continuas en el tiempo, discretas en amplitud": la se�al �nicamente puede tomar, a lo largo del tiempo, valores de un cierto conjunto, que en este ejemplo, son los n�meros enteros 0, 1, 2, 3, 4, 5... etc. Los cambios entre los valores enteros pueden ocurrir en cualquier instante (este hecho es lo que la hace continua en el tiempo).
En la figura II.2 se ilustra una se�al x(t) que es continua en el tiempo y continua en amplitud, y una se�al y(t) que es continua en el tiempo pero discreta en amplitud.
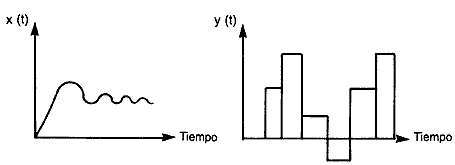
Por otra parte, ambas clases de se�ales tienen un valor determinado para cada valor del tiempo. Sin embargo, existe la posibilidad de que una se�al adquiera valores �nicamente en ciertos instantes de tiempo (por ejemplo, cada segundo, cada minuto o cada a�o). Esto puede deberse, ya sea a que as� es el fen�meno f�sico asociado, o bien porque no se tienen los mecanismos para medir las caracter�sticas de las se�ales m�s que en determinados instantes. Para ilustrar esta clase de se�ales, denominadas "discretas en el tiempo", a diferencia de las primeras que son "continuas en el tiempo", supongamos que la se�al de inter�s proviene de las im�genes captadas por una c�mara de cine. Una c�mara de cine toma en realidad fotograf�as fijas a raz�n de entre 24 y 30 fotograf�as por segundo (esta velocidad es lo suficientemente grande como para enga�ar al ojo humano y dar la impresi�n de que se trata de im�genes de objetos en movimiento). En este ejemplo se trata de muestras de im�genes en movimiento, captadas lo suficientemente r�pido como para que su contenido de informaci�n no se pierda. Este fen�meno, interesante e importante dentro de las telecomunicaciones, se denomina teorema del muestreo. H. Nyquist lo postula de la siguiente manera:
| No es necesario observar todo el tiempo una se�al anal�gica o continua en el tiempo para poder decir cu�l es su valor en cualquier momento, aunque la se�al no haya sido observada en ese instante. Es suficiente observar sus valores en instantes suficientemente cercanos entre s�, para poder reconstruir la se�al de la misma manera que si no se hubiera dejado de observar la se�al en ning�n instante. La restricci�n es que el tiempo entre las observaciones (t�cnicamente �stas se conocen como las "muestras" de la se�al) debe ser lo suficientemente peque�o para poder captar aun las variaciones m�s r�pidas |
Este principio, si bien no es v�lido universalmente, s� es lo suficientemente general para ser aplicable a una gran cantidad de se�ales (las se�ales que de alguna manera son de inter�s pr�ctico), y, de hecho, es uno de los pilares de las telecomunicaciones digitales (esto ser� analizado m�s adelante). Sus implicaciones son muy profundas: por ejemplo, en lugar de tener que guardar toda la evoluci�n de una se�al a lo largo del tiempo, es suficiente guardar un conjunto de las muestras de la se�al, sin perder la posibilidad de reconstruir toda la se�al a partir de sus muestras.
En el ejemplo de la c�mara de cine, cada cuadro de la pel�cula que representa una imagen fija de la escena filmada es una muestra de la realidad continua, y la reconstrucci�n de la se�al a partir de dichos cuadros o muestras fijas la realizan el ojo y el cerebro humanos de manera tal que el observador en ning�n momento se percata de la naturaleza discreta de lo que est� viendo.
En la figura II.3 se ilustra una se�al anal�gica x(t), as� como su versi�n muestreada, que designaremos x[mT], donde las muestras ocurren en los instantes en que el tiempo t toma los valores T, 2T, 3T..., etc. Estos instantes se llaman tiempos de muestreo, y al tiempo entre muestras consecutivas se le llama intervalo de muestreo.
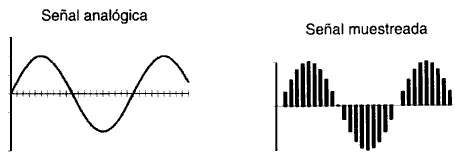
Finalmente, cuando una se�al discreta en el tiempo s�lo puede tomar valores de amplitud discretos, entonces se trata de una se�al discreta tanto en el tiempo como en amplitud. Este tipo de se�ales ha cobrado una gran importancia en las comunicaciones digitales, ya que los sistemas modernos de telecomunicaciones son eficientes y efectivos precisamente debido a este tipo de se�ales. A las se�ales que son discretas en el tiempo y en amplitud se les denomina se�ales digitales, y cuando la amplitud de la se�al solamente puede tomar uno de dos valores entonces se trata de una se�al digital binaria.
Antes de seguir con la identificaci�n y clasificaci�n de las se�ales vale la pena introducir el concepto de sistema; por una parte, esto facilitar� las explicaciones que siguen, y por la otra, es por medio de un sistema como se procesan las se�ales para realizar lo que de ellas se espera.
Se denomina "sistema" al conjunto de componentes o dispositivos del mundo f�sico que interact�an entre s�, que aceptan se�ales como entradas, las transforman y generan otras se�ales a su salida. En la figura II.4 x(t), S[x(t)], y(t), representan, respectivamente, la entrada al sistema, el sistema que transforma la se�al de entrada, y la salida del sistema.
Figura II.4. Entrada x(t), sistema S y salida y (t).
Un sistema puede ser visualizado como una caja negra del mundo f�sico que transforma la se�al a su entrada para generar la se�al a su salida.
Los siguientes son ejemplos sencillos de sistemas, y en cada caso se identifica cu�l es la entrada y cu�l la salida:
a) Equipo de sonido. La entrada es una se�al de m�sica (codificada
el�ctrica, mec�nica u �pticamente) que puede provenir de un disco fonogr�fico
(conocido coloquialmente como LP), una cinta magn�tica, un disco
compacto o una antena de radio; la salida es una se�al de audio. De hecho, el
equipo de sonido puede ser considerado como un conjunto de sistemas, donde las
salidas de unos son las entradas de otros; por ejemplo, el primer sistema puede
ser el tocadiscos de CD. Su entrada es una se�al grabada precisamente
en el CD; esta se�al es procesada �pticamente por el sistema, y
se genera a la salida una se�al el�ctrica que a su vez es la entrada del amplificador.
La salida del amplificador es una r�plica de la entrada. Si adem�s se cuenta
con altavoces, entonces la se�al el�ctrica amplificada es convertida por los
altavoces en r�plicas ac�sticas.
b) Televisor. La entrada es una se�al el�ctrica proveniente
de una antena, de un cable o de una videograbadora, y la salida es una se�al
visual en la pantalla del televisor y una se�al ac�stica en los altavoces de
�ste.
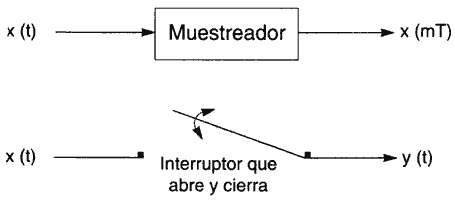
c) Muestreador. Este sistema, mencionado en p�rrafos anteriores, tiene
como entrada una se�al continua en el tiempo, y a su salida una se�al discreta
en el tiempo, donde cada muestra tiene una amplitud igual o proporcional a la
de la se�al original en el tiempo de muestreo (figura II.5).
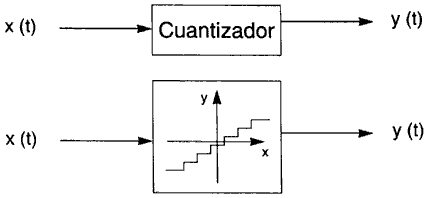
d) Cuantizadores. Tambi�n tienen funciones importantes en las telecomunicaciones. Visto como sistema, la entrada a un cuantizador es cualquier se�al continua, y la salida es una versi�n cuantizada de la misma; si la entrada es continua en el tiempo y en amplitud, la salida es continua en el tiempo, pero discreta en amplitud (figura II.6).
Los ejemplos del equipo de sonido y el televisor ilustran que es posible interconectar sistemas, de manera tal que la salida de unos sean las entradas de otros, generando de esta manera sistemas m�s generales. En la figura II.7 se ilustra la conexi�n en serie de dos sistemas S1 y S2. Se puede observar que la salida de S1 es la entrada de S2, y que la salida de S2 es la transformaci�n que realiza la conexi�n de ambos sistemas sobre la entrada de S1.
Figura II.7. Cascada de sistemas.
Habiendo establecido los conceptos b�sicos de un sistema es posible hablar ahora con m�s detalle sobre las se�ales digitales. Una se�al digital es discreta en el tiempo, y �nicamente puede tomar valores de un conjunto finito de s�mbolos o valores (cuando el n�mero de s�mbolos es 2, por ejemplo, 0 y 1, se trata de una se�al binaria). La forma de convertir se�ales digitales en general a se�ales binarias ser� tratada m�s adelante.
Una se�al digital puede provenir de los siguientes tipos de fuentes: 1) Una fuente discreta en el tiempo, que genera se�ales digitales, como n�meros, letras o texto. Estas se�ales son digitales porque los n�meros o letras que genera la fuente (s�mbolos de la fuente o alfabeto de la fuente) s�lo pueden pertenecer a un conjunto finito de s�mbolos. Si son n�meros decimales, cada s�mbolo que genera la fuente unicamente puede ser un n�mero perteneciente al conjunto 0, 1, 2, 3..., 9. Si son letras del abecedario, cada s�mbolo puede ser una letra del conjunto A, B, C..., X, Y Z. 2) Una fuente que genera se�ales discretas en el tiempo y continuas en amplitud, caso en el cual hay que generar una se�al discreta en amplitud a partir de las se�ales continuas. Para realizar este proceso, se necesita cuantizar cada valor de la fuente, es decir, aproximar cada valor continuo por medio de uno discreto. La cuantizaci�n puede ser, por ejemplo, por redondeo de cada muestra, es decir, redondeando cada valor continuo al valor discreto m�s cercano (m�s adelante se ver� esto con m�s detalle). 3) Una fuente continua en el tiempo y continua en amplitud. En este caso es necesario muestrear la se�al continua, para posteriormente cuantizarla de acuerdo con lo descrito anteriormente (figura II.6).
Como ya se ha mencionado en repetidas ocasiones, aunque una se�al contiene informaci�n de inter�s en alguna de sus caracter�sticas —por ejemplo, en la variaci�n respecto al tiempo de la amplitud o la duraci�n—, no debe ser confundida con la informaci�n que contiene. En la figura II.8 se presentan dos se�ales que aparentemente tienen la misma forma, pero que difieren en su duraci�n; de hecho, estas dos se�ales podr�an corresponder a un "punto" y una "raya" de una se�al telegr�fica.
Partiendo entonces de las ideas anteriores, y estando claro que, si bien una se�al contiene informaci�n, no es lo mismo una se�al que la informaci�n que �sta contiene, cabe plantearse la siguiente pregunta: �en qu� parte o en qu� caracter�stica de una se�al est� contenida la informaci�n? La respuesta a esta cuesti�n ha sido una de las razones de ser de los ingenieros en telecomunicaciones de las �ltimas d�cadas. M�s espec�ficamente, ha habido un inter�s definitivo en la manera de hacer que una se�al contenga la informaci�n de inter�s en alguna de sus caracter�sticas, tratando de que ello ocurra de manera eficiente y econ�mica.
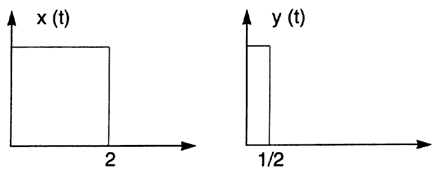
Figura II.8. Se�ales iguales en forma pero con distinta duraci�n.
Para profundizar m�s en esto es importante introducir el concepto de una se�al senoidal. Recu�rdese que y(t) representa una se�al; se dice que una se�al z(t) es una se�al senoidal, cuando su representaci�n es del tipo:
z(t) = a(t) sen wt
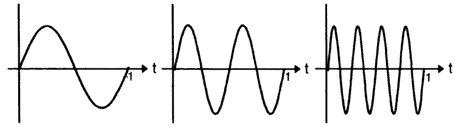
En esta expresi�n, a(t) es la amplitud de la se�al (en este momento se puede suponer que a(t) es una constante, es decir, a(t) =a; sen representa la funci�n trigonom�trica del seno; t es el tiempo; y w la frecuencia de la se�al. En la figura II.9 se ilustran se�ales senoidales en las cuales a = 1, y la frecuencia w toma los valores 1, 2 y 4. Se puede apreciar que cuando w = 4 la frecuencia de la se�al es mayor que cuando w = 1, y esto se traduce en una variaci�n mucho m�s r�pida de la se�al respecto al tiempo. La frecuencia de una se�al se mide en hertz (Hz), en memoria de H. Hertz, quien por primera vez estudi� el fen�meno, o bien en kilohertz (1 kHz = 1000Hz), o incluso, megahertz (1 MHz = 1 000 000 Hz). Un Hz representa una variaci�n de un ciclo completo en un segundo; 1 MHz representa 1 mill�n de ciclos por segundo.
Aparte de que por s� mismas son de gran inter�s matem�tico, la importancia de las ondas o se�ales senoidales radica en que, en un conjunto de condiciones generales, muchas se�ales pueden ser expresadas como la suma de ondas o se�ales senoidales (v�ase figura II.10). Este hecho fue establecido en 1822 por el matem�tico J. Fourier (1768-1830). Un ejemplo ilustrativo de la composici�n de se�ales por medio de ondas senoidales es la m�sica generada por �rganos o sintetizadores electr�nicos: las tonalidades que generan son la suma de distintas combinaciones de tonos "puros". En ingenier�a de comunicaciones, una se�al senoidal (de una sola frecuencia) es lo que en ac�stica (se�ales auditivas) ser�a un "tono puro".
No todas las personas pueden escuchar las frecuencias m�s altas (tonos agudos) generados por el �rgano, y hay combinaciones de tonos que al o�do de una persona le parecen agradables y al de otra desagradables. En la ingenier�a de comunicaciones a este fen�meno se le conoce como respuesta en frecuencia de un sistema (en este caso, del o�do humano). El rango de frecuencias contenidas en una se�al se conoce como el ancho de banda de la se�al. Por ejemplo, existen peque�os silbatos que generan tonos de frecuencias muy altas, que no pueden ser escuchados por el promedio de los seres humanos porque las frecuencias son m�s altas que las que su o�do les permite percibir (son de "ultrasonido", es decir, "de un sonido m�s all� de los que el o�do percibe"), pero que se usan para dar �rdenes a los perros, que s� perciben dichos sonidos, lo cual quiere decir que el o�do de un perro tiene una respuesta en frecuencia m�s amplia que el o�do de un ser humano.
Para ilustrar a�n m�s este concepto, consid�rese por ejemplo, la m�sica reproducida por medio de un equipo electr�nico. Normalmente, al ser humano le parece m�s agradable, m�s real, la m�sica reproducida por medio de un equipo que tenga el calificativo de "alta fidelidad". Ello significa que este equipo es capaz de reproducir se�ales cuyas frecuencias son tan altas que un equipo que no es de "alta fidelidad" no alcanza a reproducirlas, pero que en una sala de conciertos s� podr�a escuchar. En una sala de conciertos, la informaci�n la generan los instrumentos musicales; las vibraciones mec�nicas producidas por ellos son transportadas en lo que com�nmente se conoce como ondas ac�sticas que llegan a los o�dos del auditorio. Es interesante notar que cada uno de los instrumentos puede generar en cualquier instante de tiempo un tono de cualquier frecuencia o combinaciones de ellas (dentro de un rango especificado por una frecuencia m�nima y una m�xima), y con cualquier intensidad, nuevamente en un rango de intensidades m�nima y m�xima.
Un equipo de alta fidelidad debe ser capaz de reproducir se�ales hasta de 20 kHz (que est� por arriba de la frecuencia m�xima que percibe el o�do humano), y los silbatos para perros a que se ha hecho referencia generan tonos cuyas frecuencias son del orden de 30 kHz.
As� como una se�al puede ser caracterizada por su dependencia respecto al tiempo, tambi�n existe la posibilidad de caracterizarla de acuerdo con las se�ales senoidales que pueden ser sumadas para formar la se�al. Esto se conoce como "espectro en frecuencia de la se�al". Se entiende por el "ancho de banda de una se�al" la cantidad de frecuencias que est�n contenidas en una se�al.
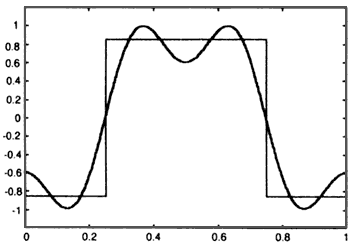
Para entender estos conceptos, analicemos la posibilidad de transmitir m�sica utilizando una l�nea telef�nica. Realizando este experimento se puede comprobar que no es posible transmitir m�sica de alta fidelidad por este canal, debido a que la m�sica tiene componentes en frecuencia cercanos a 20 kHz, mientras que el canal telef�nico s�lo es capaz de transmitir tonos hasta de cerca de 4 000 Hz. Los 20 kHz son el ancho de banda de la se�al, y los 4 000 Hz son el ancho de banda del canal telef�nico. Si se realiza el experimento, se notar� que la m�sica que se escucha difiere de la versi�n original; a este efecto se le conoce como "distorsi�n": la m�sica de alta fidelidad es distorsionada por el canal telef�nico. El efecto de transmitir una se�al de gran ancho de banda por un canal de un ancho de banda menor se ilustra en la figura II.11.
Como parte de esta introducci�n a las se�ales y los sistemas, se presentan a continuaci�n algunos problemas interesantes en los sistemas de telecomunicaciones, que se resuelven procesando una se�al por medio de alg�n tipo de sistema:
a) Amplificaci�n de una se�al. Como ya se vio anteriormente,
un amplificador es un sistema que tiene a su salida una r�plica de la se�al
de entrada, cuya amplitud fue amplificada por el sistema.
b) Suma de se�ales. Este sistema tiene dos o m�s se�ales de entrada,
y la salida de este sistema es precisamente la suma de las entradas (figura
II.12).
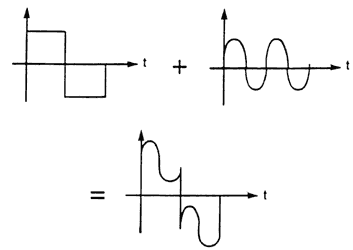
Figura II.12. Suma de se�ales.
c) Multiplicador de se�ales. Este sistema, como el anterior,
tiene dos o m�s se�ales de entrada, y la salida es el producto de ellas. Se
conoce tambi�n con el nombre de modulador de amplitud (figura II.13), ya que,
si una de las se�ales (de baja frecuencia) multiplica a otra de alta frecuencia
(portadora) la salida del sistema genera un espectro igual al de la se�al moduladora,
pero trasladado a la frecuencia de la portadora. Esto es la base de lo que se
conoce como AM (amplitud modulada o modulaci�n de amplitud). En
este proceso se "sobrepone" el contenido de informaci�n de la se�al moduladora
sobre otra se�al (portadora).
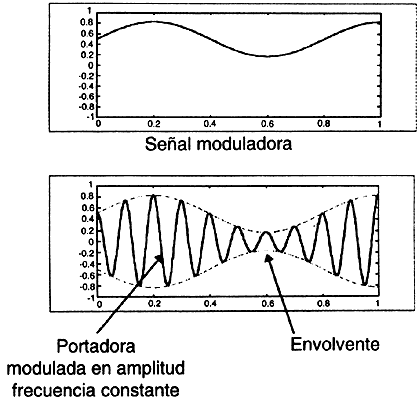
Figura II.13. Modulaci�n en amplitud y en frecuencias.
d) Codificaci�n de la fuente. Este sistema fue mencionado en la introducci�n, y realiza el procesamiento necesario para convertir una se�al anal�gica (continua en el tiempo y en amplitud) en una se�al digital. Este sistema consiste en la conexi�n en serie de un muestreador, un cuantizador y un codificador (figura II.14).
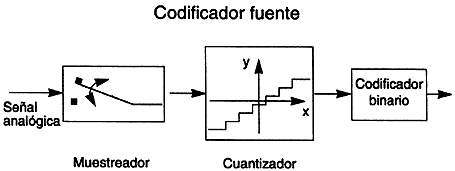
Figura II.14. Codificador fuente.
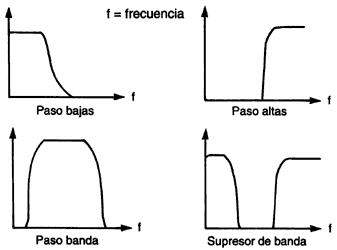
e) Filtrado. Por medio de un filtro se eliminan ciertas componentes de frecuencia de una se�al. Un ejemplo de esto fue planteado al hablar de la posibilidad de transmitir m�sica por un canal telef�nico. Existen diversos tipos de filtros que, dependiendo de la porci�n del espectro que eliminen, pueden ser paso-bajas (eliminan las frecuencias altas), paso-altas (eliminan las frecuencias bajas), paso-banda (s�lo dejan pasar frecuencias dentro de una banda) o supresor de banda (eliminan las componentes dentro de una banda). Estos filtros se ilustran en la figura II.15. Cabe mencionar que, en las figuras, si en alguna o algunas frecuencias la amplitud es cero, esto significa que de la se�al de entrada se eliminan todas las componentes en las frecuencias donde esto ocurre, generando de esta manera la se�al filtrada.
Para concluir este cap�tulo, es indispensable hablar sobre el peor enemigo de las telecomunicaciones: el ruido (a pesar de ser enemigo de las telecomunicaciones, es un aliado de los ingenieros en telecomunicaciones, ya que, de no haber ruido en las transmisiones, no habr�a ingenieros cuya funci�n fuera eliminar su efecto).
As� como en el lenguaje cotidiano el ruido es aquello que molesta, que perturba, que impide realizar alguna tarea, el "ruido' en las telecomunicaciones es todo aquello que modifica el contenido de informaci�n de una se�al. Como la fuente desea que la informaci�n llegue a su destino lo m�s parecida a aquella generada por la fuente, el hecho de que se introduzca ruido act�a en contra del proceso de comunicaci�n. El ruido en las telecomunicaciones es, por lo tanto, una distorsi�n: en el sonido, en el caso de la telefon�a; en la imagen, en el caso de la televisi�n; errores, en el caso de la telegraf�a, etc. No es posible hasta el momento tener un sistema de comunicaciones en el cual no haya ruido. Pero, por fortuna, los distintos procesos de ruido en los canales han sido modelados matem�ticamente, de manera tal que estos modelos reflejen con verdad la realidad y, por lo tanto, el efecto del ruido pueda ser disminuido. En la figura II.16 se muestran se�ales que corresponden a muestras de ruido.
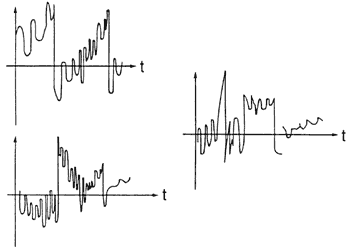
Se puede apreciar que en todos los casos las representaciones del ruido tienen trayectorias que son aleatorias, dif�cilmente predecibles, por lo cual es necesario recurrir a modelos probabil�sticos para su an�lisis. Para apreciar realmente lo que es el ruido, conviene "sintonizar" un radiorreceptor en una frecuencia en que no haya ninguna transmisi�n, preferentemente en AM. Como puede escucharse, existe una especie de "zumbido", que es precisamente el ruido en el canal.
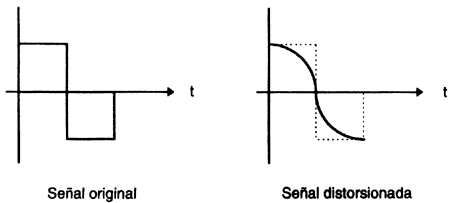
Aunque el ruido puede afectar de diversas maneras una transmisi�n (sum�ndose o multiplic�ndose con la se�al que contiene la informaci�n), en este libro se analizar�n �nicamente casos en que el efecto del ruido es aditivo. Esto se ilustra en la figura II.17, donde se muestra una se�al binaria (que toma valores positivos o negativos), el ruido en la transmisi�n y la suma de la se�al m�s el ruido.
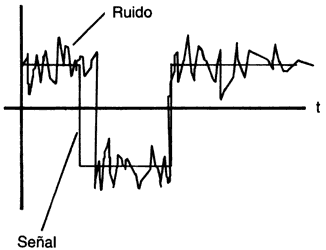
Las ideas anteriores permiten plantear un problema adicional de las telecomunicaciones y que se presenta principalmente en las comunicaciones en que las se�ales son digitales. Supongamos que se transmite una se�al binaria a trav�s de un canal ruidoso, tal como se presenta en la figura II.17, al recibirse la se�al en el receptor, la se�al que fue transmitida tiene una forma diferente a la que se transmiti�. Entonces, una de las principales funciones del receptor consiste en tomar una decisi�n, basada en la se�al distorsionada, acerca de la se�al que se transmiti�: �se trata, en cada instante, de un "1" o se trata de un "0"? Este problema se conoce con el nombre de "detecci�n". El problema de detecci�n tambi�n tiene mucha importancia en algunos aspectos de navegaci�n a�rea: como ser� analizado m�s adelante, el sistema conocido como "radar" (que significa radio detection and ranging, es decir, detecci�n y medici�n de distancias por radio) consiste en la emisi�n de pulsos electromagn�ticos de duraci�n corta; cuando en su trayectoria encuentran alg�n obst�culo, parte de la energ�a se refleja en dicho objeto extra�o, y esa energ�a reflejada, a su vez, es recibida en una central. Como la se�al reflejada normalmente contiene poca energ�a, tiene una amplitud peque�a, que puede ser distorsionada con facilidad por el ruido atmosf�rico. Entonces es necesario tomar una decisi�n entre las dos siguientes posibilidades: �la se�al recibida proviene de una onda reflejada, o se trata �nicamente de ruido?
Hasta aqu� han sido presentados conceptos fundamentales acerca de las se�ales y de los sistemas m�s importantes en las telecomunicaciones. Estos conceptos ser�n integrados en los siguientes cap�tulos para formar sistemas completos de telecomunicaciones; por lo tanto, frecuentemente se har� referencia a este material a lo largo del presente libro.
