IX. MÁS SOBRE EL CAOS

EN ESTE capítulo se examinará una forma diversa de considerar al fenómeno caótico. Regresemos al caos de la población que tratamos en el capítulo anterior. Vimos que si el valor del parámetro q de la ecuación (6) es suficientemente pequeño, entonces, sea cual sea el valor inicial de la población, es decir, el valor inicial de x, después de cierto número de iteraciones se llega a un valor final que ya no cambia al seguir iterando. Recordando que cada iteración nos da el valor de la población un año después, concluimos que si q es suficientemente pequeño, después de cierto tiempo se llega a una población final que ya no varía al transcurrir el tiempo.

Si q aumenta, ocurre que después de ciertas iteraciones la cantidad x adquiere dos valores. En una iteración adquiere el primero, y en la siguiente, el segundo, y estos dos valores se van alternando. Esto significa que después de cierto tiempo, en un año la población tiene un valor y al siguiente el segundo valor. En el tercero la población vuelve a tener el primer valor, en el cuarto el segundo valor, y así sucesivamente. Por lo tanto, el primer valor final lo adquiere la población cada dos años; lo mismo ocurre con el segundo valor, la población lo va adquiriendo cada dos años. Este era el régimen que se llama de periodicidad dos.

Al seguir aumentando el valor de q se llega a un régimen final en el que hay cuatro posibles valores finales de la población, que se van alternando. Por tanto, cada uno de estos valores se va adquiriendo cada cuatro años. Estamos en el caso de la periodicidad cuatro.

Podemos así continuar, hasta que se llegue al régimen caótico, en que cada año la población va adquiriendo cierto valor que ya no se repite.

Ahora bien, lo anterior significa que, antes de entrar en el régimen caótico, el periodo va aumentando de 1 a 2 años, a 4 años, a 8 años, etc., a medida que el valor de q va aumentando. Llega cierto momento en que ya no se puede hablar de periodo, se ha entrado en el régimen caótico.

Otra forma de presentar estos resultados es en términos de la frecuencia y no del periodo. Estas dos cantidades están íntimamente relacionadas. El periodo es el tiempo que tarda algún fenómeno en volverse a repetir, por ejemplo, el tiempo en que tarda la Tierra en dar una vuelta alrededor de su eje es el periodo de su rotación. Como sabemos este periodo es de 24 horas. Es claro que para poder hablar de periodo el fenómeno debe ser repetitivo, esto es, periódico.

La frecuencia de un fenómeno periódico es el número de veces que se repite en un segundo, en un minuto o en otra unidad de tiempo. Si un tocadiscos da 33 vueltas por minuto, esto significa que su frecuencia es de 33 revoluciones por minuto, abreviado 33 rpm.

Un ejemplo de fenómeno repetitivo es cuando un cuerpo se mueve alrededor de un círculo. Supongamos que el cuerpo tarda 5 segundos en dar una vuelta; su periodo es de 5 segundos. Por lo tanto, en un segundo el cuerpo habrá dado (1/5) de vuelta; su frecuencia es (1/5) = 0.2. De este ejemplo vemos que si el periodo tiene cierto valor, llamémosle T, entonces su frecuencia es igual a (1/T). La frecuencia es igual al inverso del periodo.

Regresando al caso de la población que estudiamos antes, llegamos a la conclusión de que al ir aumentando el valor de q el periodo aumenta a 2, luego a 4, luego a 8, y así sucesivamente, hasta llegar al régimen caótico. Expresando esto en términos de frecuencia, vemos que si para un valor de q solamente hay un periodo esto equivale a un valor de la frecuencia.

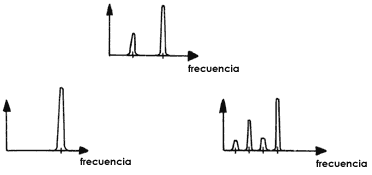
Figura 20. Gráficas que muestran las frecuencias características que gobiernan el fenómeno para valores recientes de q. A medida que q crece, aumenta el número de frecuencias.

Al aumentar el valor de q, el periodo aumenta al doble y por tanto, la frecuencia disminuye entonces a la mitad.

Al seguir aumentando el valor de q, el periodo aumenta cuatro veces, por lo que la frecuencia disminuye cuatro veces.

Al continuar aumentando el valor de q, el periodo aumenta ocho veces, por lo que la frecuencia disminuye ocho veces, etcétera.

En consecuencia, si para cada valor de q se hiciera una gráfica de la frecuencia que corresponde al fenómeno, se encontraría la sucesión de gráficas de la figura 20. Cada gráfica de esta sucesión corresponde a un valor de q. Vemos entonces que los picos de las gráficas, a medida que q aumenta, van apareciendo a la mitad del valor de la frecuencia anterior. Cuando se llega al régimen caótico, entonces ya no hay ningún pico, ya que no hay periodo, y por tanto, no hay ninguna frecuencia característica.

Una forma de obtener resultados experimentales, como en el caso de la turbulencia, es por medio de análisis de frecuencias del fenómeno en cuestión. Este es el motivo por el cual introdujimos la explicación en términos de esta cantidad.