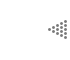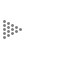XII. ARITMÉTICA. LA SECUENCIA DE FIBONACCI
VAMOS a formar una secuencia de números de la siguiente forma.
Empecemos con el cero y el uno; si los sumamos nos da:
Sumemos ahora el 1 de la derecha con el anterior 1 del lado izquierdo:
Ahora sumemos este 2 con el 1 que está a la izquierda, antes del signo igual:
y seguimos formando la secuencia, sumando el resultado con el último número del lado izquierdo:
2 + 3 =5 |
3 + 5 = 8 |
5 + 8 = 13, |
De esta manera se forma la secuencia llamada de Fibonacci, que es,
Esta secuencia tiene características aritméticas muy interesantes y, sin haberse pretendido, tiene aplicaciones importantes, como veremos.
En primer lugar, multipliquemos cada número de la secuencia por el número 1.6. Así se obtiene la siguiente secuencia:
Si ahora redondeamos cada uno de estos números al entero más cercano encontramos:
que a partir del segundo 2 es ¡precisamente la secuencia de Fibonacci! (a excepción de unos términos iniciales y posiblemente algunos posteriores). Esto es, resulta que la secuencia de Fibonacci es autosimilar.
Ahora vamos a construir otra secuencia, a partir de la de Fibonacci, como sigue. Tomamos un número de la secuencia de Fibonacci y lo dividimos entre el siguiente. Si empezamos con el segundo, que es 1, y lo dividimos entre el tercero, que también es 1, nos da:
Ahora dividimos el tercero, que es 1, entre el cuarto, que es 2, y nos da:
Al dividir el cuarto, que es 2, entre el quinto, que es 3, nos da:
Si seguimos así obtenemos los siguientes números:
etc. Si seguimos así nos daremos cuenta de que todos los demás cocientes se van acercando al número 0.618. Este último recibe el nombre de la media dorada. Otra manera de obtenerlo es como sigue:
Sumemos 1 con 1, que nos da 2. Tomemos su inverso:
El lector se dará cuenta que lo que hizo es la operación siguiente:
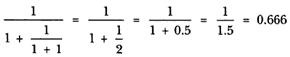
Ahora repetimos el procedimiento con 0.666. Le sumamos 1, que nos da 1.666 y tomamos su inverso:
Nótese que lo que se ha hecho hasta ahora es:
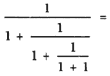
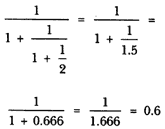
Continuando de esta manera se obtienen las siguientes formas. Le sumamos 1 a 0.6 y obtenemos 1.6. Su inverso es:
Este valor también se puede escribir como sigue:
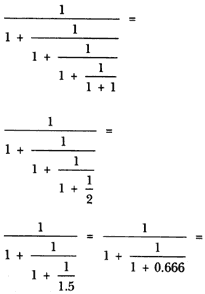
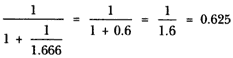
Si se continúa con este procedimiento llega un momento en que se obtiene el número 0.618. Continuando, le sumamos 1 y obtenemos 1.618. Su inverso es:
¡Otra vez 0.618! Por tanto, al continuar con el procedimiento obtendremos todo el tiempo 0.618. En la figura 23 se muestra la forma de encontrar este número 0.618, que recibe el nombre de la media dorada.
A este tipo de quebrados se les llama fracciones continuas. Por lo tanto, la media dorada se obtiene también como una fracción continua. En la figura 23 vemos que es geométricamente autosimilar.
La secuencia de Fibonacci fue obtenida por primera vez en 1202 por el matemático italiano Leonardo de Pisa, hijo de Bonacci (en italiano, figlio de Bonacci, o Fibonacci, nombre que se le quedó), al tratar la cuestión del crecimiento de una población de conejos. Se hizo la pregunta de cuántas parejas de conejos habrá después de cierto número de temporadas de crianza, esto es, cómo se multiplican los conejos. Para simplificar supuso lo siguiente:
1) Se empieza con una pareja inmadura.
2) Los conejos maduran una temporada después de haber nacido.
3) Las parejas de conejos maduras producen una nueva pareja cada temporada de crianza.
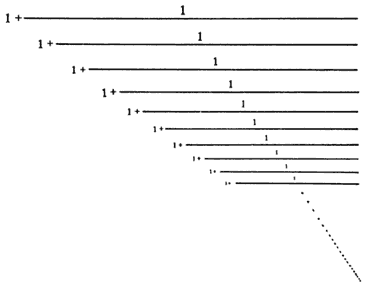
Figura 23. La sucesión de operaciones para obtener la media dorada es autosimilar.
De acuerdo con estas reglas, el número de conejos en una generación es igual a la suma de las parejas de conejos que hay en las dos generaciones anteriores. Si se empieza con una pareja, después de una temporada se produce una nueva pareja. Por tanto, al final de la temporada hay 1 + 1= 2 parejas de conejos. Si se sigue de esta manera se encuentran los siguientes números de parejas en las sucesivas temporadas:
que es precisamente la secuencia de Fibonacci.
Otra manera de ver lo anterior es como sigue: vamos a llamar con el número 0 a una pareja inmadura y con el 1 a una pareja madura. Por tanto, después de una temporada una pareja inmadura (0) producirá una pareja madura (1), o sea, donde hay un 0® 1. Además, una pareja madura (1) produce una pareja inmadura (0) y, por lo tanto, después de esta temporada existirán la pareja madura (1) y la inmadura (0). En consecuencia, después de una temporada donde hay un 1® 10. Con esta regla de transformar unos y ceros, veamos qué se obtiene al transcurrir las temporadas.
Si empezamos con 0® 1; este 1®10; el último 1®10, y el 0 se transforma en 1, por lo que el 10® 101. Transformando cada uno de estos números de acuerdo con la regla que dimos:
Este último número se transforma, a su vez, en:
y así seguimos indefinidamente. De esta forma se obtiene la secuencia siguiente
llegando después de muchas temporadas, al número:
¿Es esta secuencia autosimilar? En este número vamos a subrayar las parejas "10":
Si en lugar de cada pareja "10" subrayada sustituimos ahora un "1", y en lugar de cada "1" no subrayado sustituimos un "0", encontramos lo siguiente:
Esta secuencia la podemos ver gráficamente como sigue (figura 24). Dibujemos una pareja inmadura en blanco, y una pareja madura en negro. Al principio hay sólo una pareja inmadura (renglón 1). Después de una temporada, esta pareja llega a la madurez (renglón 2) y, además de seguir viviendo, produce una pareja inmadura después de una temporada. Por tanto, en la tercera temporada (renglón 3) hay una pareja madura y una inmadura.
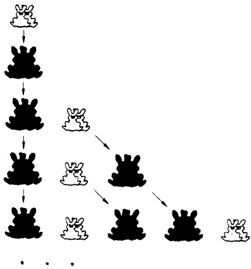
Figura 24. Una pareja inmadura se muestra en blanco y otra, madura, en negro.
Son los resultados que se obtienen en cada temporada.
Siguiendo con este razonamiento, se muestran en la figura 24 las poblaciones en varias temporadas posteriores. Si ahora representamos una pareja inmadura (en blanco) con el "0" y a una madura (en negro) con el "1", se van obteniendo las siguientes secuencias
que son precisamente las secuencias que vimos arriba. El lector se dará cuenta de que una pareja inmadura (0) produce una pareja madura (1), o sea, 0 ®1. Además, después de una temporada, una pareja madura (1) produce una inmadura (0), por lo que al final de la temporada quedan la madura (1) y la inmadura (0), o sea, 1 ® 10. Estas transformaciones son precisamente las que se usaron arriba