XIII. CUASICRISTALES

UNA consecuencia obtenida al aplicar el concepto de la autosimilitud fue lograr la predicción de la existencia de una nueva fase de la materia, a saber, los cuasicristales. Haremos una breve revisión de algunos conceptos referentes al estado sólido.

La materia se encuentra a nuestro alrededor formando diferentes fases: la gaseosa, la líquida y la sólida.

En la fase gaseosa, los átomos o moléculas se mueven y giran totalmente al azar. Esto da como consecuencia que el gas no tenga ninguna estructura.

En un líquido los átomos también están desordenados. En un sólido se dan varias posibilidades. En un caso importante los átomos se encuentran situados al azar, o sea desordenados; éste es un sólido amorfo. Un ejemplo son los vidrios.

En otros sólidos, los átomos se encuentran formando redes periódicas, dando lugar a un cristal. Muchas sustancias sólidas conocidas son cristales, como la sal de mesa, formada por átomos de cloro y de sodio (figura 25) o los diamantes. En un cristal los arreglos son periódicos, lo que significa que se repiten. Además, en un cristal hay simetrías, lo que significa que si se traslada el cristal a determinada distancia, entonces el patrón se repite. Por ejemplo, en la figura 26 se muestran redes cristalinas en dos dimensiones (debido a que se encuentran en un plano, el de la hoja). Si se traslada cualquiera de ellas adecuadamente, se vuelve a repetir la red.

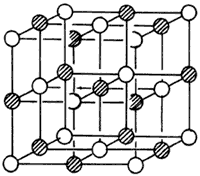
Figura 25. Esquema de un cristal. Nótese que cada celda se va repitiendo.

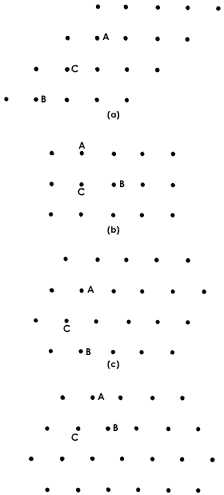
Figura 26. Simetrías de un cristal en dos dimensiones: (a) simetría de 180°=360°/2; (b) simetría de 90°=360/4; (c) simetría de 120°=360°/3 y (d) simetría de 60°/6. No hay simetría de 360°/5=72°.

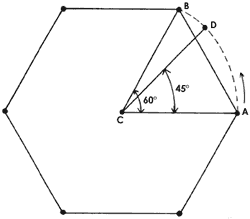
Figura 27. Una celda en que los átomos ocupan los vértices de un hexágono tiene simetría de 60°=360°/6.

Nos damos cuenta de que cada una de estas redes tiene una simetría. Esto quiere decir que si se gira la red por cierto ángulo alrededor de un punto que esté en el centro del "azulejo", se vuelve a recuperar la red. Por ejemplo, en el caso de la figura 27, que está formada de "azulejos" hexagonales, si se gira el patrón alrededor del punto C en un ángulo de 60°, el punto A cae en el punto B, que es un punto de la red. Si el ángulo que se girara fuera de 45° digamos, entonces el punto A caería en el punto D, que no es punto de la red, y ésta no se reproduciría. Decimos que la red hexagonal tiene simetría de 60° = 360°/6. Para los casos de la figura 26, al girar el punto A alrededor de C al ángulo anotado a continuación, llega al punto B, que es un punto de la red. Las simetrías son entonces:

a) figura 26(a): 180°= 360°/2; b) figura 26(b): 90° = 360°/4; c) figura 26(c): 120°= 360°/3; d) figura 26(d): 60° = 360°/6.

En la teoría del estado sólido se demuestra que, en el caso de dos dimensiones, éstas son las únicas posibles simetrías.

Un caso prohibido es la simetría de 5, o sea la que resultaría de un giro de 360&3176/5 = 72°. La demostración es la siguiente: supóngase que los puntos A y B sean puntos de una red, en que la distancia AB sea la mínima en el cristal (figura 28(a)). Los puntos A y B están entonces ocupados por átomos. Si hubiera simetría de 72°, esto querría decir que si se gira el cristal, con centro en el punto A, por un ángulo de 72° (figura 28(b)) entonces el punto B caería en el punto C, que debería ser ocupado por un átomo. De la misma forma, al girar el cristal por un ángulo de 72° alrededor del punto B (figura 28(c)), el punto A caería en el punto D, que también debería ser ocupado por un átomo. En consecuencia, los puntos C y D también serían puntos de la red cristalina (figura 28(d)). Vemos que la distancia CD es menor que la distancia AB. Pero se partió del hecho de que la mínima distancia entre dos átomos es la distancia AB. Por lo tanto se llega a una contradicción, hecho que indica que no puede darse este tipo de simetría.

Lo que hemos mencionado para el caso de dos dimensiones, también se aplica en el de tres dimensiones. No todas las simetrías son posibles.

Durante muchos años así lo pensaron los científicos e ingenieros. Sin embargo, en 1984 se anunció el descubrimiento de la fase de una aleación de aluminio-manganeso que tiene simetría de 72°. Esto se descubrió por medio del patrón de difracción de electrones mostrado en la figura 29. La muestra se bombardea con un haz de electrones y se registran en una película las direcciones de los electrones que salen de la muestra.* Solamente diremos que este patrón refleja las simetrías que tiene la sustancia. Se puede ver en la figura 29 que si se gira el patrón alrededor del centro un ángulo de 72ñ, se vuelve a recuperar el patrón original. Es decir, hay simetría de 72°.

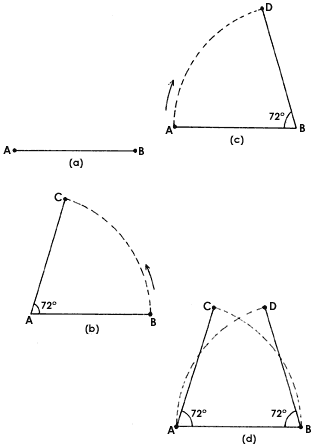
Figura 28. Demostración de que la simetría de 72° = 360°/5 no es posible.

La pregunta que inmediatamente surgió fue: ¿cómo es posible llenar el plano con cierta figura de manera completa? Si nos fijamos en la figura 26(b) vemos que con la celda cuadrada es posible llenar completamente un plano. Por este motivo es que ocurre la simetría 4. Es posible llenar el plano con cada una de las forma de la figura 26. ¿Cómo sería posible llenar el plano para que se obtenga una simetría de 72°?

Una manera de llenar un plano con esta simetría es la mostrada en la figura 30. A primera vista la figura da la impresión de ser periódica. Sin embargo, a diferencia de lo que pasa con las formas de la figura 26, si nos fijamos con detenimiento, veremos que ahora ya no hay periodicidad. A este tipo de estructura se le llama cuasicristal.

Se han descubierto también cuasicristales de tres dimensiones, mas no hablaremos de ellos.

Figura 29. Patrón de difracción de electrones en una muestra de aluminio-manganeso que tiene la simetría de 72° = 360°/5.

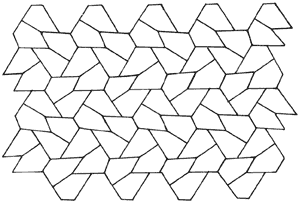
Figura 30. Forma en que se puede llenar todo el plano con figuras que tiene la simetría de 72°. Nótese que esta estructura no es periódica.

Pero, ¿qué tiene que ver todo esto con la autosimilitud? Para contestar esta pregunta vamos a construir, en primer lugar, una red de una dimensión, es decir; a lo largo de una línea recta. Para este fin consideremos primero una red cuadrada como la que se muestra en la figura 31(a). Ahora tracemos una línea recta (figura 31(b)) que forme con el eje horizontal un ángulo de 58.280. Esta línea es la LK. Al lector que sepa trigonometría le diremos que este ángulo es tal que su tangente es igual a (1/0.618) = 1.618, donde 0.618 es la media dorada de la que se trató en el capítulo anterior. Es decir, el ángulo de 58.28° está relacionado con la media dorada.

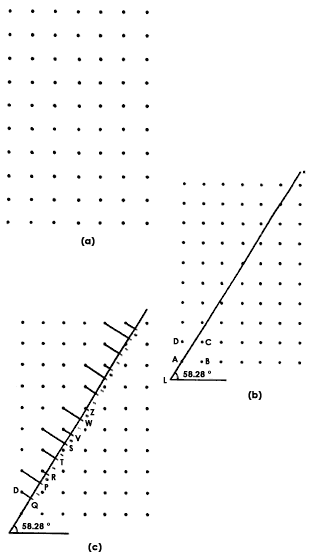
Figura 31. Procedimiento de construcción de un cuasicristal a lo largo de una línea recta. En el texto se ilustra la importancia de la media dorada para esta constucción.

La línea recta LK cruza varios cuadrados de la red, como por ejemplo, el ABCD. Ahora bien, cada vez que la línea entre en un cuadrado, desde el vértice superior izquierdo se trazará una línea perpendicular a la línea recta. Así, en el cuadrado ABCD, el vértice superior izquierdo es D; desde D se traza la línea DQ, perpendicular a la línea LK De esta manera se forman en la línea los puntos Q, P, R, T,S,... y resulta que las distancias QP, RT, TS sólo adquieren dos valores. Las distancias QP, RT, TS son iguales entre sí; asimismo, las distancias PR, SV, WX, ... son también iguales entre sí. De las dos distancias que se forman, una es más grande que la otra. Por ejemplo, PR es menor que QP. Resulta que la relación entre estas dos distancias diferentes que así se forman es:

ñigual a la media dorada! Si llamamos longitud grande igual a "1" y a la pequeña igual a "0", entonces las longitudes en las que se divide la línea transversal, a partir de Q, son (figura 31(c)):

1011010110110...

que es precisamente la secuencia de Fibonacci, que se trató en el capítulo anterior (véase (A) de la página 72). Si ahora consideramos la línea LK y en los puntos Q, P, R,... se colocan átomos, se forma un cuasicristal en una dimensión.

Para los casos de dos y tres dimensiones se puede hacer algo análogo. Sin embargo, esto implica consideraciones en las que no entraremos y solamente diremos que se puede hacer con ayuda de una computadora. Para el caso de dos dimensiones lo que se obtiene es el arreglo mostrado en la figura 32. Si uno se fija con cuidado, los puntos de esta red no forman una red periódica. Resulta que estos puntos corresponden a los vértices de la red mostrada en la figura 30. Nótese que esta red cubre completamente todo el plano pero no es periódica.

Por otro lado, el patrón de difracción de electrones que produce una red como la mostrada en la figura 32 es ñprecisamente el patrón mostrado en la figura 29! En consecuencia, el patrón de la figura 29 obtenido experimentalmente, corresponde a una red con simetría de 72°.

Figura 32. Cuasicristal construido en dos dimensiones siguiendo el procedimiento correspondiente a la figura 31 en un plano.

Podemos afirmar que las redes que se construyeron en las figuras 31(c) y 32 son cuasicristales, en una y dos dimensiones, respectivamente.

De la manera en que se construyeron estos cuasicristales vemos que llevan inmersos dentro de sus estructuras una característica de autosimilitud, que se encuentra en la secuencia de Fibonacci.