XXII. ECONOMÍA ¿ES POSIBLE GANAR EN LA BOLSA DE VALORES?

TODOS los días se ven en la sección financiera del periódico gráficas que muestran el comportamiento del índice de precios de la bolsa de valores, como la que aparece en la figura 44, que muestra alzas y bajas aparentemente sin regularidad, al azar.

Para mucha gente, en particular las que invierten dinero en la bolsa de valores, es de interés poder predecir la tendencia y, si fuera posible, el precio de las acciones, ya que si tuvieran esta información podrían comprar o vender con ventaja y así ganar dinero.

Desde hace mucho tiempo los economistas han intentado estudiar y comprender los movimientos de precios en la bolsa de valores. ¿De qué depende que una acción suba o baje?

Los economistas han supuesto, en general, que la variación de los precios de algún producto, por ejemplo el algodón, tiene dos componentes: una de largo alcance, en el que los precios se regirían por fuerzas económicas profundas como la apertura de rutas comerciales, inventos que utilizaran el producto, una guerra, alguna innovación tecnológica que modificara el uso del producto, una revolución, etc. Esta tendencia a largo alcance, meses, años o décadas, quedaría determinada de manera muy clara.

La otra componente del precio sería de corto alcance: los precios variarían al azar, debido a un número muy grande de causas, muchas de las cuales no se podrían determinar con precisión. Estos vaivenes, llamados fluctuaciones, son transitorios. Se ha pensado que casi no hay relación entre los dos ritmos de largo y de corto alcance.

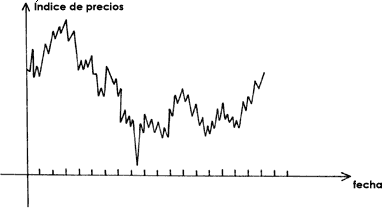
Figura 44. Gráfica de los índices de precios en la bolsa de valores de un periodo determinado. Parece que las alzas y bajas no tienen regularidad alguna.

Figura 45. Curva gaussiana

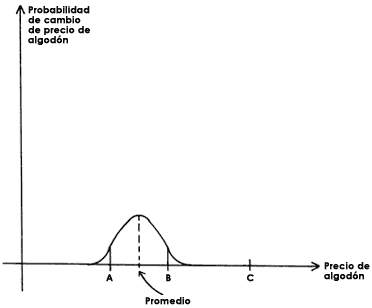
Se ha considerado que las variaciones de los precios, a largo alcance, siguen una ley determinada, como la que se muestra en la figura 45 y que grafica la probabilidad del cambio en el precio de, por ejemplo, el algodón. Esta curva, llamada curva gaussiana, tiene forma de campana y nos dice que la mayoría de los cambios ocurrirá cuando el precio esté dentro de los límites marcados entre los valores A y B, alrededor de un valor promedio. Así, por ejemplo, la probabilidad del valor C, muy lejano del intervalo AB, es muy pequeña. La distribución gaussiana se utiliza en muchos campos en los que hay variables al azar. Por ejemplo, si se miden las longitudes de los clavos de un paquete que nominalmente deberían tener una longitud de 20 cm, se encontraría que no todos tienen efectivamente esta longitud. Resulta que, si el paquete es grande, la distribución de longitudes toma una forma gaussiana, centrada alrededor de 20 cm. Es decir, la mayoría de los clavos tiene una longitud, si no de 10 cm, sí muy cercana a 20 cm. Una longitud de 45 cm tiene una probabilidad extraordinariamente pequeña de ocurrencia. Este es el significado que tiene la distribución gaussiana.

Sin embargo, en el intento de sobreponer los precios que el algodón adquirió de 1880 a 1958 se encontró que no se ajustaban a una curva gaussiana. Se hicieron muchos intentos de hacer este ajuste, todos ellos sin éxito.

El mismo fracaso se alcanza al analizar los precios de diferentes acciones en la bolsa de valores, en la que también se ha pensado que existen dos tipos de ritmos casi independientes entre sí: largo y corto alcance.

Fue Mandelbrot el primero que vio los valores de los precios del algodón desde otra perspectiva, y se preguntó: ¿por qué deberían los precios del algodón, o para el caso de cualquier otra entidad económica, tener una distribución gaussiana? Es más, ¿por qué debería haber una separación tan cortante, como lo que se proponía, entre largo y corto alcance?

Una de las suposiciones implícitas que los economistas hicieron al trabajar con la distribución gaussiana es que los precios cambian continuamente. Esto significa que si hay una variación en el precio de una acción de $100 a $40, entonces el precio debe pasar por todos los valores intermedios, o sea, la acción debe adquirir los valores de $87.5, $55, $49.75, etc. Esto desde luego no es cierto. Mandelbrot hizo la suposición de cambios discontinuos en los precios y llegó así a la predicción de la distribución de precios que se muestra en la figura 46, en la cual se dibuja la gráfica, en el eje vertical, de una cantidad relacionada con la variación de precios, y en el eje horizontal, de los precios. La predicción hecha es la curva continua y los valores de los datos que tenía de las variaciones de los precios del algodón se muestran por medio de puntos. El conjunto de puntos marcados con 1 corresponde a cambios positivos de los precios diarios del algodón. El conjunto de puntos marcado con 2 corresponde a cambios positivos de los precios mensuales; el conjunto marcado con 3 corresponde a cambios de los precios anuales. Los conjuntos 4, 5 y 6 corresponden a cambios negativos en los precios diarios, mensuales y anuales, respectivamente.

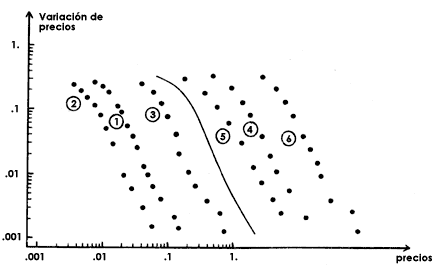
Figura 46. Comparación entre la variación de precios en distintas circunstancias (conjuntos de puntos) con las predicciones (líneas continuas). Cada línea corresponde a una escala de tiempo distinta.

Nótese que los distintos conjuntos de puntos corresponden a escalas de tiempo muy diferentes. Si se copiara esta gráfica en un acetato transparente y se trasladara la curva predicha (línea continua), se superpondría en cada uno de los conjuntos empíricos formados por los puntos. Es decir, la misma predicción resulta ser válida a lo largo de diferentes escalas: diaria, mensual y anual. No hay diferencias entre las escalas temporales como se ha pensado. Esto significa que hay similitud y que la estructura de los precios es fractal. Si en lugar de hacer una gráfica como la de la figura 44, en que se muestran las fluctuaciones de los precios de las acciones en la bolsa de valores a lo largo de un día, se hiciera la gráfica a lo largo de un mes, o de un año, se encontrarían gráficas que tienen la misma forma, o sea, son similares.

Doyne Farmer, Norman Packard y James McGill en Nuevo México, EUA, han llevado este análisis de la economía mucho más adelante, considerando que la dinámica que rige los fenomenos económicos es no lineal. Un efecto de ésta es que una causa pequeña puede producir efectos muy grandes. Un ejemplo es la conocida fábula del camello muy cargado al que, en cierto momento, se le añade una pajita y se rompe su espalda. La paja es en extremo liviana, pero el peso extra que añade tiene una consecuencia fuera de toda proporción. Esto se debe a que su efecto NO queda determinado por una simple relación entre el peso de la paja y el peso del camello, sino a una interacción muy complicada entre todos los factores que afectan al camello, como los objetos que ya está cargando, si durmió bien la noche anterior, la temperatura del desierto, etc. Es decir, una pequeña causa puede ejercer un gran efecto.

Si en un fenómeno hay una relación directa entre la causa y el efecto, y si ocurre que al aumentar la causa al doble el efecto aumenta al doble, entonces la relación es lineal. Claramente, en el caso de la fábula la relación entre el peso de la paja y el efecto sobre el camello no es lineal.

Si se considera el patrón de tráfico de vehículos en una ciudad grande y se quisiera poder hacer predicciones, una manera de proceder sería aprender todo lo que se pudiera sobre cada vehículo individual, todas sus velocidades y todos los sentidos de las calles, etc. Sin embargo, esta forma de proceder no permitiría hacer predicciones de tráfico. Si un conductor frena porque un niño se le atraviesa, podrían darse repercusiones a varios kilómetros de distancia. Es decir, este fenómeno es no lineal.

Si, por otro lado, se observa el tráfico desde cierta altura, por medio de un helicóptero, uno se podría dar cuenta de que hay un flujo y sería posible hacer predicciones a futuro, por lo menos para intervalos cortos. Nótese que el observador del helicóptero no necesita información detallada acerca de las características de cada uno de los vehículos.

Las personas que manejan las acciones en la bolsa de valores son análogas a los coches y por medio de relaciones no lineales, como las que consideramos en el capítulo VIII, se pueden entender tendencias a corto alcance del comportamiento de los precios de las acciones de la bolsa de valores.

Debido a que la dinámica de los precios es no lineal, como ya sabemos, en estos casos existe un régimen caótico. Entender este hecho ha permitido a algunas personas hacer predicciones a corto alcance, de unos cuantos días, sobre el comportamiento de los precios. Es más, en 1991, Farmer, Packard y McGill fundaron una compañía, The Prediction Company (Compañía de Predicciones) que se dedica a analizar la evolución en el tiempo de los precios de diferentes acciones de la bolsa de valores. Se basan en la teoría del caos, algunos de cuyos elementos se trataron en el capítulo VIII. Son capaces de hacer predicciones que abarquen unos cuantos días sobre el comportamiento de precios, y los resultados se los proporcionan a sus clientes.

Para tener una idea de cómo trabajan, diremos que toman como base lo siguiente: regresando al tema tratado en el capítulo VIII, estudiaremos el caso en que q = 3.6 y como valor inicial de x tomemos 0.6. Como vimos, este valor de q corresponde a la región caótica. Al iterar en la misma forma que se hizo en el capítulo VIII, los valores de x que se obtienen, como lo puede comprobar el lector son, sucesivamente: 0.6, 0.756, 0.664, 0.803, 0.569, 0.883, ... 0.437, 0.886, 0.364, 0.834, 0.499, 0.900, ...

Supongamos que se nos diera el valor de 0.437, con éste podríamos predecir que los siguientes tres valores de x son: 0.886, 0.364, 0.834. Si por algún motivo, como es lo que ocurre en el caso de la economía, no se conoce la función (6) con cuya ayuda encontramos estos números, entonces hay procedimientos matemáticos más complicados para encontrar los resultados, no de todas, pero sí de las iteraciones inmediatas. Con este espíritu proceden en The Prediction Company.

La manera matemática completa como se han podido hacer predicciones no está todavía suficientemente desarrollada. Fundamentar y completar este trabajo todavía tomará tiempo. Sin embargo, llevan una gran delantera sobre quienes analizan la evolución de precios a la manera tradicional.

The Prediction Company mantiene en secreto los procedimientos que utiliza en sus predicciones. Lo que se puede decir es que han ganado mucho dinero —ellos y sus clientes— en la bolsa de valores.

Se podría pensar que si toda la gente que participa en la bolsa de valores supiera que, por ejemplo, el jueves el precio de una acción va subir, entonces el miércoles antes del cierre todos comprarían, y por tanto, el precio subiría no el jueves, sino el miércoles, y por tanto, la predicción no serviría. Es decir, el comportamiento en la bolsa de valores es tal, que si uno encuentra un patrón, al actuar lo elimina. Esto no ocurre en un fenómeno físico.

Sin embargo, la filosofía de los miembros de la compañía de la que estamos hablando es otra. Lo que pasa es que si se dice que se tiene una nueva idea, lo prudente sería esperar a ver si efectivamente ocurre. Dejar pasar cierto tiempo y no actuar. Si todo funciona bien, quien la emplee tendrá buenas ganancias y, en el momento en que los demás quieran aprovechar esta idea, deja de funcionar. El resultado neto es que el primero en idear y usar tal sistema sí ganó dinero.