III. EJEMPLOS DE ALGUNAS COSAS RARAS

UNA situaci�n que nos parece com�n es medir alguna longitud; como la de una costa, entre dos puntos A y B (figura 1).

Figura 1. �Cu�l es la longitud de la costa entre los puntos A y B?

Una manera de hacerlo ser�a medir la longitud de una l�nea recta que une A con B (figura 2). Sin embargo, la costa es, en general, irregular, por lo que es claro que su longitud ser� mayor que la de la l�nea recta entre sus dos puntos extremos. Podr�amos ahora tomar como unidad una barra arbitraria de longitud H, por ejemplo. Para medir la longitud de la costa llevar�amos esta barra a lo largo de la costa (figura 3) y contar�amos las veces que la barra cabe a lo largo de la costa desde A hasta B. A este n�mero, denotado por L₁, le llamamos la longitud de la costa.

Nos damos cuenta inmediatamente de que tal n�mero en realidad no es el valor de la longitud de la costa, ya que por ejemplo, entre los puntos A y C donde cay� la barra la primera vez, la longitud de ese tramo de costa no es la de la barra.

Para mejorar nuestra medici�n tomamos otra barra, de menor longitud, digamos de la d�cima parte de la anterior, H/10, y repetimos el procedimiento obteniendo para la longitud de la costa el n�mero L₂. Nuevamente podemos afirmar, por el mismo argumento que dimos arriba, que no es exactamente la longitud de la costa.

Podemos continuar indefinidamente de esta manera, tomando unidades cada vez m�s y m�s peque�as. Intuitivamente esperar�amos que la sucesi�n de valores que se obtengan para las longitudes de la costa, medidas de esta manera, tender�a a alcanzar un valor bien definido que ser�a la "verdadera" longitud de la costa. Sin embargo, esto no ocurre. De hecho, lo que sucede es que esta sucesi�n de longitudes aumenta cada vez m�s y m�s. Es decir, al seguir el procedimiento indefinidamente, la longitud de la costa que se mide se va haciendo cada vez m�s y m�s grande, esto es, �la longitud de la costa entre A y B tiende a un valor infinito!

Este resultado sorpresivo se puede explicar como sigue: si primero observamos la costa en un mapa de escala 1/100 000 nos daremos cuenta de que tiene algunas bah�as y pen�nsulas. Si en seguida volvemos a examinar la misma costa, pero ahora en un mapa que tenga la escala de 1/10 000, es decir, en una escala m�s amplia, aparecer�n caracter�sticas que no se ve�an en el mapa anterior. As�, ahora se ven nuevas bah�as y nuevas pen�nsulas. Si se sigue examinando la costa, pero en un mapa que est� a una escala todav�a m�s grande, digamos de 1/1 000, aparecer�n nuevas bah�as y pen�nsulas que no se ve�an en ninguno de los mapas anteriores. As� podemos continuar indefinidamente.

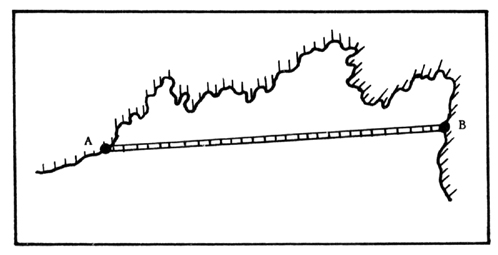
Figura 2. La distancia recta entre A y B no es la longitud de la costa.

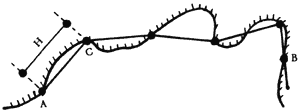
Figura 3. Con la barra de longitud H se mide cu�ntas veces �sta cabe entre A y B.

En consecuencia, al ir cambiando de escala, como van apareciendo m�s y m�s bah�as y pen�nsulas peque�as, �stas contribuyen a la longitud que se est� midiendo. Por muy chica que sea la nueva bah�a o pen�nsula, al ir aumentando la escala, en alg�n momento aparecer� en el mapa y contribuir� a la longitud de la costa.

Si uno cambiara el m�todo de medici�n de la longitud, tambi�n se llegar�a a la misma conclusi�n.

Otro ejemplo de este tipo de situaci�n ocurre al tratar de medir la frontera entre dos pa�ses. Se puede dar un argumento an�logo al que presentamos arriba para la bah�a y se llega a la misma conclusi�n: �la frontera entre dos pa�ses tiene, en rigor, longitud infinita!

En 1961 el ingl�s L. F. Richardson present� una serie de las mediciones experimentales que hizo de varias costas, fronteras y cuerpos geom�tricos regulares. En cada caso fue cambiando el valor de la unidad de medida H; de esta forma obtuvo el correspondiente valor de la longitud L que denotamos como L(H), pues depende de la unidad H. En la figura 4 se muestran algunos de sus resultados. Se puede apreciar que al ir disminuyendo el valor de H la longitud L va aumentando. Sin embargo, se puede ver que la variaci�n de L en ciertos intervalos de H no es muy pronunciada.

Podemos ahora preguntarnos lo siguiente: �si aplicamos estas ideas a la medici�n del per�metro de una figura como un cuadrado o un c�rculo, no pasar� lo mismo? La l�nea (d) de la figura 4(d) muestra el valor de L para un c�rculo; se ve que L es siempre el mismo (e igual al valor del per�metro del c�rculo, tal como se ense�a en los cursos de geometr�a) en todo el intervalo de valores de H en que se hicieron las mediciones. Lo que ocurre es que en las figuras geom�tricas, al ir aumentando la escala de la observaci�n NO aparecen estructuras del tipo de bah�as o de pen�nsulas, que eran invisibles en la escala anterior, ya que por definici�n, la l�nea que delimita a la figura carece de estas estructuras. Por ejemplo, el c�rculo se define como el conjunto de puntos que dista una longitud constante del centro. Por lo tanto, en el c�rculo no puede haber algo an�logo a una pen�nsula, como en el caso de la costa.

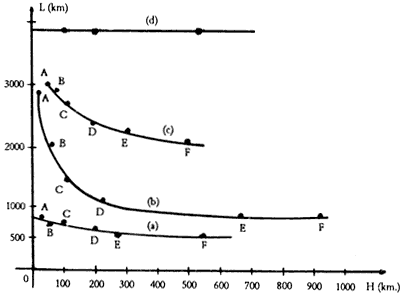
Figura 4. La longitud de varias curvas depende de la longitud de medida H. a) Frontera entre Portugal y Espa�a. b) Costa occidental de Gran Breta�a. c) Frontera terrestre alemana (1900). d) Per�metro de un c�rculo.

Aqu� vemos con claridad lo que significa la abstracci�n de la realidad que hizo Euclides, quien no consider� figuras tales como las de una costa, sino que supuso que sus l�neas no ten�an estructuras que eran invisibles en una escala y visibles en otra. Sin embargo, en la realidad, muchas l�neas que se presentan en la naturaleza s� tienen esta �ltima caracter�stica.

En este punto esperamos que el lector se sienta inc�modo. �C�mo es posible que, por ejemplo, la frontera entre dos pa�ses no est� perfectamente determinada? Pues, efectivamente, en lo que respecta a su longitud no lo est�. Richardson menciona que cada pa�s da un valor diferente a la longitud de su frontera com�n. Por ejemplo, Espa�a dice que su frontera con Portugal mide 987 km, mientras que Portugal afirma que son 1214 km; seg�n Holanda su frontera con B�lgica mide 380 km, mientras que B�lgica reclama que son 449 km. Lo que sucede es que, al hacer las mediciones, cada pa�s utiliz�, de hecho, otro valor de la unidad H, y por tanto obtuvo otro valor de la longitud.

La discusi�n anterior nos lleva a la conclusi�n inesperada de que la longitud de cierto tipo de objetos, que m�s adelante llamaremos fractales, no tiene un valor bien determinado. Su longitud depende de la unidad H que se escoja. Si dos observadores eligen dos unidades distintas obtendr�n dos resultados distintos. �Y ambos observadores tendr�n raz�n! Es decir, este tipo de mediciones no es completamente "objetivo". Es claro que, en las relaciones entre pa�ses, se debe reconocer el car�cter especial de las cantidades que se van a medir y llegar a un convenio mutuo sobre cu�l deber� ser la unidad de longitud que se debe seleccionar. De esta forma se evitar�n ambig�edades.