IV. A VECES SE ESTÁ MIRANDO ALGO PERO NO SE VE. ALGUNOS CASOS HISTÓRICOS

SI SE suelta un grano de polen en un vaso de agua se observa que realiza un movimiento desordenado e irregular. Se mueve siguiendo una trayectoria en forma de zigzag (figura 5). En un cine, en el haz de luz que envía el proyector hacia la pantalla, se puede ver que las partículas de polvo que flotan en el aire realizan también un movimiento en zigzag.

Ambos movimientos reciben en física el nombre de movimiento browniano, que fue descrito por primera vez por el botánico inglés Robert Brown en 1828.* No entraremos en la historia de este fenómeno. Sólo presentaremos algunas características de él que nos serán útiles.

Las líneas de la trayectoria de una partícula browniana (figura 5) no tienen en rigor ninguna realidad física. La forma en que se trazaron las líneas del dibujo es imaginando que cada 30 segundos se observa la posición de la partícula de polen y se marca con un punto; luego estos puntos se unen sucesivamente con líneas rectas. Por tanto, lo único que tiene realidad son los puntos, que indican las posiciones de la partícula browniana al final de cada intervalo. Si ahora, en lugar de marcar las posiciones en cada intervalo de 30 segundos se marcan en cada intervalo de 3 segundos y se unieran los puntos con líneas rectas, cada línea recta de la figura 5 quedaría reemplazada por una sucesión de líneas quebradas de menor tamaño, pero de igual complejidad. Así, por ejemplo, si nos fijamos en dos puntos sucesivos, A y B, de la figura 5, se obtendrán entre ellos los puntos mostrados en la figura 6. Si ahora unimos estos puntos con líneas rectas obtendremos las líneas quebradas de la misma figura 6. Concluimos que la segunda figura que se forma tiene el mismo tipo de estructura que la primera.

Se podrían tomar ahora intervalos más pequeños, por ejemplo, de 0.3 segundo y seguir el mismo procedimiento; ocurriría lo mismo que antes. Nos damos cuenta de que la trayectoria que sigue una partícula browniana es tal que mantiene una estructura similar al cambiar la escala de tiempos de la observación. Este tipo de línea fue denominada fractal por el científico Benoit Mandelbrot en 1975.

Figura 5. Trayectoria irregular y azarosa que sigue una partícula browniana.

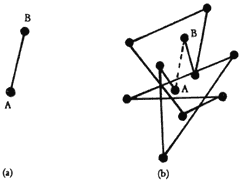
Figura 6. a) Los puntos A y B son las posiciones de la partícula Browniana al inicio y al final de un intervalo de tiempo. b) Posiciones de la misma partícula browniana al registrarla en intervalos equivalentes a la décima parte del intervalo anterior.

Es interesante mencionar que ya en 1906 el físico francés Jean Perrin se había dado cuenta de este tipo de comportamiento. En particular, había hecho notar que si uno toma un punto de la trayectoria que sigue una partícula browniana entonces, en rigor, no se puede trazar una línea tangente a ella, y apuntó entonces:

Usando lenguaje geométrico, las curvas que no tienen tangente constituyen la regla, y curvas regulares, tales como el círculo, son interesantes pero especiales.

A primera vista, la consideración del caso general puede parecer un mero ejercicio intelectual, ingenioso pero artificial. Los que oyen hablar de curvas sin tangente tienden a pensar que la naturaleza no presenta tales complicaciones, ni siquiera las sugiere.

Sin embargo, lo contrario es la verdad. Esta afirmación se puede ilustrar considerando ciertos valores experimentales sin preconcepción.

Considérese, por ejemplo, uno de los copos blancos que se obtienen al añadir sal a una solución jabonosa. A cierta distancia su contorno puede dar la sensación de estar nítidamente definido, pero a medida que nos acercarnos esta nitidez desaparece. El ojo ya no puede dibujar una tangente en cualquier punto. Una línea que, a primera vista, pareciera ser satisfactoria, bajo un escrutinio detallado resulta ser perpendicular u oblicua. El uso de una lupa o de un microscopio aún nos deja más en la duda, ya que aparecen nuevas irregularidades cada vez que aumentamos la magnificación, y nunca logramos conseguir una impresión nítida, lisa como la dada, por ejemplo, por una bola de acero...

...la característica esencial de nuestro copo es que cualquier escala incluye detalles que prohíben absolutamente la fijación de una tangente.

Quedaremos dentro de los dominios de la realidad experimental en el momento en que observemos bajo el microscopio el movimiento browniano con el que se agita una partícula (browniana) suspendida en un fluido. Se descubre entonces que la dirección de la línea recta que une las posiciones ocupadas por una partícula en dos instantes muy cercanos en el tiempo varía irregularmente en forma absoluta a medida que el intervalo entre ambos instantes se hace menor. Un observador sin prejuicios concluiría, en consecuencia, que está tratando con una curva a la que no se le puede dibujar una tangente.

Nadie hizo caso a los comentarios de Perrin, y este asunto quedó dormido hasta finales de la década 1960-1970, cuando Mandelbrot lo retomó. Hablaremos al respecto en el capítulo siguiente. Si se hubiera seguido investigando la observación hecha por Perrin a principios de siglo, lo que hoy llamamos fractales posiblemente habrían sido desarrollados 60 años antes.

Otro caso que nos será de interés en este libro es el del científico francés Henri Poincaré. Para entender su proposición, olvidada durante cerca de 70 años, recordaremos algunos hechos.

Las leyes del movimiento de Isaac Newton, expuestas a fines del siglo XVII, implicaban que si se conoce la fuerza que se aplica sobre una partícula se puede conocer la trayectoria que seguirá. Sin embargo, esta posibilidad contiene una condición: que se debe poder especificar qué posición y qué velocidad tenía la partícula en el instante inicial. Es decir, si se pueden precisar las condiciones iniciales de la partícula, las leyes de Newton permiten conocer completamente su futuro, lo cual resultará válido para cualquier sistema que tenga cualquier número de partículas.

Basado en estos hechos, el matemático francés Pierre Simon de Laplace (1749-1827) llegó a jactarse de que si se le dieran las posiciones y velocidades iniciales de cada una de las partículas que componen el Universo, podría predecir el futuro por el resto del tiempo. Este hecho conlleva un riguroso determinismo en las leyes de la naturaleza. Las inferencias de estas conclusiones acerca de las leyes de Newton las trataremos en un capítulo posterior.

En el año de 1903 Poincaré escribió lo siguiente:

...nosotros solamente podemos conocer la situación inicial de manera aproximada. Si esto nos permitiera predecir la situación que sigue en el tiempo con la misma aproximación, es todo lo que necesitaríamos, y podríarnos decir que el fenómeno ha sido predicho, que está regido por leyes. Pero esto no es siempre así; puede ocurrir que pequeñas diferencias en las condiciones iniciales produzcan condiciones muy diferentes en los fenómenos finales. Si un pequeño error en las condiciones iniciales produce un enorme error en las condiciones finales, la predicción se vuelve imposible y tenemos un fenómeno fortuito.

En el capítulo VII se analizará con mayor detalle este comentario.

Al igual que en el caso de Perrin, las observaciones de Poincaré permanecieron olvidadas durante muchos años; ningún científico les puso atención. Si se hubiera continuado trabajando en este campo desde esa época, es posible que el caos como teoría científica se hubiera desarrollado muchas décadas antes.

Éstos son dos ejemplos de situaciones que no son muy raras en la historia de la ciencia. Algún científico se da cuenta de cierto fenómeno, pero por diversos motivos nadie se ocupa de él y cae en el olvido, lo que ilustra el hecho de que el desarrollo de la ciencia no es tan objetivo como se quisiera pensar.