V. LOS FRACTALES. NUEVAS DIMENSIONALIDADES
EN LAS últimas dos décadas se ha desarrollado una línea de investigación,
iniciada por Benoit Mandelbrot, cuyo tema son los objetos llamados fractales.
Se puede construir un tipo de figuras fractales siguiendo el siguiente ejemplo. Tomemos un triángulo equilátero cualquiera (figura 7(a)) al que se denominará iniciador. Divídase cada lado en tres partes iguales. En las partes intermedias de cada lado añádanse dos lados de un triángulo equilátero cuyo lado sea igual a la tercera parte del lado original. Se obtiene así la figura 7(b). Enseguida, divídase otra vez cada uno de los lados de la figura así formada en tres partes iguales, y en cada parte intermedia añádanse dos lados de un triángulo equilátero cuyo lado sea igual a la longitud resultante. Se encuentra así la forma mostrada en la figura 7(c). Si se continúa indefinidamente este procedimiento se encontrará una forma parecida a la mostrada en la figura 7(d). Esta figura es un fractal y, como veremos a continuación, su perímetro tiene longitud infinita.
Analicemos con un poco de detalle el perímetro de estas figuras. Supongamos que el lado del triángulo iniciador de la figura 7(a) sea igual a 1 (en cualquier unidad). El perímetro del triángulo original, que es igual a la suma de las longitudes de sus lados, es entonces igual a 8.
Por construcción, cada línea recta de la figura 7(b) tiene longitud (1/3). Por tanto, dado que hay 12 líneas rectas de este tamaño, el perímetro de la figura 7(b) es 12 x (1/3) = 4. El lector se dará cuenta de que este nuevo perímetro (4) es mayor que el original (3).
Veamos ahora la figura 7(c). Cada línea recta de esta figura tiene (1/9) de longitud. En vista de que hay 48 de estas líneas, su perímetro es 48 x (1/9) = 5.333, mayor que los perímetros de las figuras 7(a) y 7(b).
Vemos entonces que la sucesión de valores de los perímetros es: 3, 4, 5.333,...
Esta sucesión va creciendo. La causa de que crezca es clara, ya que de un paso
al otro el número de líneas rectas aumenta más rápidamente de lo que disminuye
la longitud de cada línea recta. De hecho, en cada paso de la construcción el
número de líneas se multiplica por el factor 4, mientras que la longitud de
cada línea disminuye 3 veces. Por lo tanto, el perímetro se multiplica, de un
paso al otro, por el factor 4 x (1/3) = 1.333, que es un número mayor que 1.
Si el número de pasos es infinito, el perímetro de la figura así formada también
resulta ser infinito.
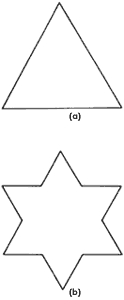
Figura 7. Pasos que siguen para construir el fractal llamado curva de Koch.
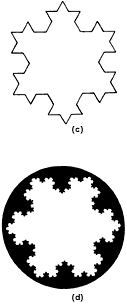
Figura 7. Pasos que siguen para construir el fractal llamado curva de Koch (continuación).
La curva de la figura 7(d) se llama curva de Koch.
Nos debemos dar cuenta de que si se comparan las figuras que se forman en dos construcciones sucesivas, se verá que ambas tienen la misma estructura. Se recordará del capítulo III que lo mismo ocurre con la bahía cuando se cambia la escala.
Un objeto que presenta la misma estructura al cambiársele indefinidamente la escala de observación recibe el nombre de fractal. Por lo tanto, la curva de Koch y la bahía son fractales.
Mandelbrot asegura que en la naturaleza existen muchos fenómenos de carácter fractal, de hecho, muchos más de los que podemos imaginar. Mencionaremos en forma breve algunos.
La trayectoria que sigue una partícula que realiza movimiento browniano, descrita en el capítulo IV es un fractal. En efecto, al pasar de una escala a otra, como por ejemplo, cuando se pasa de la figura 5 a la 6, las estructuras son similares.
También los paisajes naturales presentan características de los fractales.
Así, la forma de las cadenas montañosas (figura 8) da lugar a que si uno intentara
medir su superficie encontraría valores infinitos. Una manera de crear un paisaje
fractal es la siguiente. Tomemos el triángulo de la figura 9(a). El punto medio
de cada lado lo desplazamos cierta cantidad (figura 9(b)). Así el punto A se
traslada al punto B; el punto G al D, y el E al F. Uniendo los puntos B, D y
F con los vértices del triángulo se forman cuatro triángulos más pequeños que
el original, como se ve en la figura 9(c). Si se sigue este procedimiento muchas
veces con cada uno de los triángulos formados, se logra obtener una figura que
tiene todo el parecido a una montaña (figura 8). Un programa de computadora
llena los triángulos resultantes con sombreados apropiados que le dan un toque
en extremo realista a la figura.

Figura 8. La forma de una cadena montañosa es un fractal.
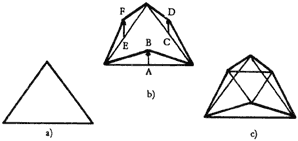
Figura 9. Pasos para construir un paisaje fractal.
En la geometría euclidiana se enseña que hay una relación determinada entre, por ejemplo, el área que ocupa una figura y la longitud de la línea que encierra a dicha área. Así, por ejemplo, para un cuadrado, la longitud de su perímetro elevada al cuadrado es igual a 16 veces el área encerrada. En efecto, supongamos que el lado del cuadrado es de 3 cm. Entonces el perímetro es:
Si se eleva al cuadrado se obtiene:
Por otro lado, el área del cuadrado de lado 3 cm es:
| perímetro² = 16
x área. |
(1) |
En un cuadrado, el perímetro al cuadrado es igual a 16 veces el área encerrada.
Si se trata de un círculo, la longitud del perímetro elevada al cuadrado es igual a cuatro veces p (la letra griega pi) por el área encerrada:
| perímetro² = 4p
x área. |
(2) |
Recuérdese que el número p (pi) es igual a 3.14159...
De manera general, el cuadrado del perímetro de una figura geométrica es igual al área encerrada, multiplicada por un número. Este número depende de la forma particular de la figura que se esté tratando: para el cuadrado el número es 16 y para el círculo 4p.
Un tipo de relación análoga se encuentra entre el volumen de un cuerpo y el área de la superficie que lo encierra. En efecto, se puede demostrar que en una figura cúbica el cubo del área es igual a 216 veces el cuadrado del volumen encerrado. Por ejemplo, si el lado de un cubo mide 2 cm, entonces el área total del cubo es 6 veces el área de cada cara, ya que tiene 6 caras. Pero el área de cada cara es (2 cm) x (2 cm) = 4 cm². Por tanto:
Elevemos ahora este valor al cubo:
Por otro lado, el volumen del cubo se obtiene elevando al cubo la longitud de su lado:
Elevando al cuadrado este valor:
| área³ = 216 x volumen². |
(3) |
Para otro tipo de figuras, el factor que multiplica al (volumen)² no es 216, este coeficiente depende de la figura particular de que se trate.
En el caso de las figuras que son fractales, las relaciones que obtuvimos no se satisfacen. Consideremos, por ejemplo, el caso del cerebro de los mamíferos; se sabe que su corteza presenta numerosas circunvoluciones. De mediciones hechas con mucha precisión resulta que la relación entre el volumen del cerebro y el área de la superficie que lo encierra no sigue el patrón mencionado arriba para las figuras geométricas regulares. Se encuentra ahora que el cubo del área ya no es proporcional al volumen elevado al cuadrado, sino que:
| área³ = A x volumen
a, |
(4) |
donde A es un número, análogo al 216 de la ecuación (3), pero el exponente a (alfa) no es igual a 2 como en la ecuación (3) sino que tiene un valor entre 2.73 y 2.79.
Se puede demostrar que de esta relación puede inferirse que la superficie que encierra al cerebro es fractal. Este resultado se ha explicado en relación con las necesidades que la evolución va creando para los mamíferos.
De hecho, cuando en una figura se satisface la relación (3) entre su área y su volumen, la figura es euclidiana. Si no, como en el caso del cerebro que se está considerando, entonces es fractal.
Otro ejemplo del campo biológico se da en la estructura nasal de algunos animales. La membrana que cubre el hueso de la nariz es tal, que la relación entre área y volumen encerrado no sigue un patrón geométrico euclidiano, sino fractal. Ciertos animales tienen esa membrana con un área muy grande para el volumen que encierran. La membrana podría estar relacionada con el sentido del olfato y, por ejemplo, en el caso de los camellos su gran área les ayudaría a localizar; husmeando, el agua tan escasa en el desierto.
La descarga y el nivel de las crecidas de los ríos son otro ejemplo de fractales. Resulta que estas cantidades, tomadas anualmente, tienen valores muy persistentes. Se ha intentado dar, infructuosamente, diversas explicaciones a este hecho. Aparentemente la única explicación que tiene visos de conformarse con los resultados experimentales es que estas cantidades se comportan como fractales.
También se han aplicado las ideas de los fractales a la economía. Un análisis detallado del comportamiento en el cambio de precio de las mercancías muestra que su estructura es análoga a la de un fractal. Esto se debe a que al cambiar de escalas temporales la determinación de los cambios, se encuentran estructuras similares.
En lingŁística también se producen estructuras fractales. Se ha estudiado las relaciones que sigue en un idioma la frecuencia en el uso de las palabras. Pues resulta que este comportamiento es fractal. Uno de los parámetros de este fractal da la medida de qué tan rico es el uso del vocabulario a través de la frecuencia relativa del uso de palabras poco comunes.
Se ha determinado que los fractales también se dan en la teoría de los circuitos eléctricos y en la teoría de la información, por mencionar sólo algunos campos. Se han abierto de esta manera vastos horizontes de estudio y aplicación que apenas empiezan a explorarse.
El hecho de que en las figuras regulares, las que trata la geometría euclidiana, la relación entre el cuadrado del perímetro y el área (véanse las ecuaciones (1) y (2) de la página 28), o bien, entre el área al cubo y el cuadrado del volumen (véase la ecuación (3) de la página 29) se dé con exponentes que son números enteros (por ejemplo, el 3 del área al cubo y el 2 del cuadrado del volumen) se debe a que se está tratando con una, dos y tres dimensiones. Sin embargo, cuando se trata de fractales (véase la ecuación (4) de la página 30), entonces, como vimos arriba, ya no se tienen estas relaciones con números enteros en los exponentes. Por tanto, los fractales son figuras que no corresponden a una dimensionalidad entera.
Lo que está ocurriendo es que la geometría euclidiana, con sus dimensiones enteras, no logra alcanzar la esencia de las formas irregulares. Considérese un ovillo de cuerda. Si se le observa desde muy lejos (figura lO(a)) se le verá como un punto, es decir, una figura de dimensión nula. Si el observador se acerca verá que el ovillo ocupa un espacio parecido a una esfera, o sea, de tres dimensiones (figura 10(b)). Si el observador se sigue acercando advertirá con detalle la cuerda que forma el ovillo y éste se transforma, en realidad, de dimensión uno (figura 10(c)). Si seguimos acercándonos, es decir; nos disminuimos imaginariamente para apreciar la estructura microscópica de la cuerda, la cuerda empieza a verse nuevamente de tres dimensiones, porque se empezará a apreciar las fibras que lo componen, que podrán verse como columnas tridimensionales. Así se puede continuar. De esta manera, se aprecia que no se puede hablar de la dimensionalidad de la cuerda de una manera "objetiva". Todo depende de la perspectiva del observador, esto es, de la escala en que se haga la observacion.
Mandelbrot dio un paso muy atrevido al proponer que se asignara a los fractales
dimensiones que no fueran números enteros. La dimensión fraccionaria propuesta
constituyó una manera de poder medir de otra forma características no definidas
claramente. Por ejemplo, el grado de irregularidad de una línea, como la bahía,
o la aspereza de una superficie. Mandelbrot propuso la forma de calcular la
dimensión de un objeto fractal y demostró que el número que así se obtiene no
depende de la escala en que se hacen las observaciones. Recuérdese que si se
asignan dimensiones enteras, entonces, como en el caso del ovillo de cuerda,
la dimensión va cambiando al cambiar la escala de observación.
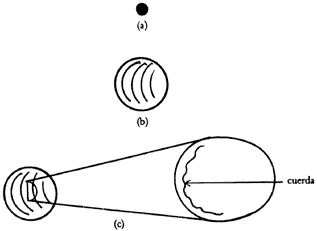
Figura 10.a) De lejos, un ovillo se ve como un punto. Su dimensión es 0;
b) más de cerca vemos el ovillo como una esfera. Su dimensión es 3; c) todavía
más cerca vemos la cuerda del ovillo. Su dimensión es 1.
 1 1 |
Figura 1-4. Sucesión de fotografías que muestran la caída de una gota de tinta en agua. Al caer la gota, se transforma en un anillo de vórtices, que se expande hasta volverse inestable, dando lugar a un nuevo anillo de vórtices. Este proceso se repite muchísimas veces, es decir se forma un fractal. En las fotografías se ven distintos estados de los fractales así formados. |
2 |
 3 3 |
4 |
 5 5 |
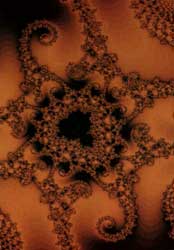
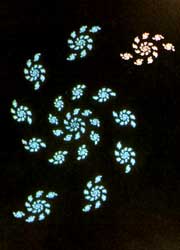
5-16. Diversos fractales generados
por computadora. En cada caso se ha utilizado un procedimiento repetitivo
diferente, como se ejemplifica en el texto. |
6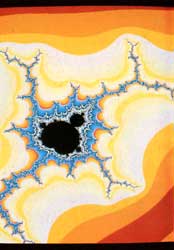 |
 7 7 |
8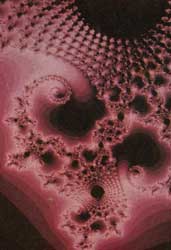 |
 9 9 |
10 |
 11 11 |
12 |
 13 13 |
14 |
 15 15 |
Fotos del Doctor Jose Luis del Río,
Departamento de Física, Universidad Autónoma Metropolitana-Iztapalapa
y de Jorge Lodigiani Rodriguez, División de Ciencias Biológicas
y de la salud Universidad Autónoma Metropolitana-Iztapalapa. |
16 |

Figura 11. La forma de una rama es fractal.
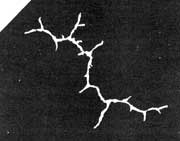
Figura 12. Un rayo tiene forma de fractal.
Por tanto, el grado de irregularidad de un fractal es el mismo a medida que se cambia de escala. Es decir; hay una irregularidad regular, valga la expresión.
Como ilustración mencionamos que la curva de Koch (figura 7(d)) tiene una dimensión igual a 1.2618.
Una de las características de un fractal es que conserva la misma forma si se le ve en distintas escalas, como en el caso de las líneas asociadas al movimiento de una partícula browniana (figuras 5 y 6). Esta característica de los fractales se llama auto similitud.
Es posible construir figuras fractales siguiendo un procedimiento bien determinado, o como se dice más técnicamente, un algoritmo, por ejemplo, el procedimiento para construir la curva de Koch. De la misma manera se puede construir una superficie que se parece mucho a la terrestre (figura 9). Este algoritmo ha sido utilizado en la filmación de películas con el fin de crear superficies. Se ha demostrado que la superficie terrestre tiene una dimensión fractal de 2.7, hecho que han utilizado muy provechosamente los geólogos.
Otros empleos son los de fabricar patrones semejantes a los del crecimiento de las especies biológicas (figura 11) o las de una descarga eléctrica como un rayo (figura 12).
En capítulos posteriores trataremos en detalle algunos de los casos mencionados, en los que aparecen objetos fractales.