VII. CONDICIONES INICIALES Y SU IMPORTANCIA

EN EL capítulo IV citamos a Poincaré cuando aludía a las condiciones iniciales. En el presente capítulo analizaremos en detalle esa cuestión.

Consideremos un fenómeno físico bien conocido, la caída de los cuerpos. Una piedra cae al soltarla debido a que experimenta una fuerza, la de gravedad, que está dirigida hacia el centro de la Tierra. Con base en las leyes de Newton se puede encontrar que la trayectoria que sigue la piedra es una línea recta vertical.

Sin embargo, la misma piedra sujeta a la misma fuerza (su peso) también puede moverse a lo largo de otra trayectoria. Por ejemplo, si la lanzamos hacia arriba formando cierto ángulo con la horizontal, entonces se moverá a lo largo de la trayectoria mostrada en la figura 13, que resulta ser una parábola.

Nos podemos hacer la siguiente pregunta: si en los dos casos la misma piedra estuvo sujeta a la misma fuerza, ¿por qué en un caso se movió a lo largo de una línea recta vertical y en el otro a lo largo de una parábola? Como podemos apreciar, a pesar de ser la misma piedra y la misma fuerza, hubo una diferencia.

· En el primer caso se soltó la piedra, lo que significa que en el instante inicial su velocidad fue nula

· En el segundo caso se le dio a la piedra, en el instante inicial, una velocidad dirigida hacia arriba, como se muestra en la figura 13.

Por tanto, en los dos casos hubo condiciones iniciales diferentes y, en consecuencia, las trayectorias seguidas fueron distintas, a pesar de que en ambos casos la piedra estuvo sujeta a la misma fuerza, la gravedad.

Este ejemplo nos ilustra un hecho muy importante: para conocer el tipo de evolución que sigue un sistema se necesita conocer, además de las leyes que lo rigen (en los casos de arriba, las de Newton y la fuerza de la gravedad), las condiciones iniciales del sistema. Bajo las mismas leyes, diferentes condiciones iniciales producen distintas evoluciones en el tiempo.

La cuestión a que se refirió Poincaré tiene que ver con lo siguiente. Tomemos dos piedras iguales. Soltemos la primera piedra desde cierto punto, digamos el A, sobre el suelo (figura 14(a)). Al mismo tiempo soltemos la segunda piedra desde el punto B, que está muy cercano al A. Nos damos cuenta de que, no obstante que en ambos casos las velocidades iniciales de las piedras son iguales (cero), sus posiciones iniciales no son iguales ya que las soltamos desde dos puntos distintos, aunque difieren muy poco. Decimos que las condiciones iniciales de ambas piedras no son las mismas, aunque sí muy parecidas.

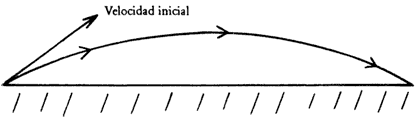
Figura 13. Una piedra lanzada hacia arriba, formando un ángulo con la horizontal, describe una trayectoria parabólica.

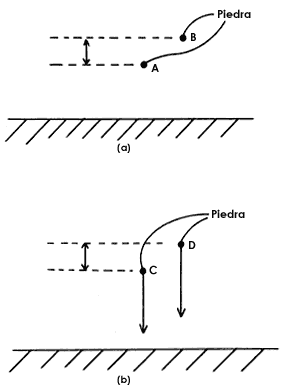
Figura 14. Cuando dos cuerpos caen a partir del reposo y desde posiciones muy cercanas, no se separan mucho en sus trayectorias.

Veamos qué pasa con las posiciones que van ocupando las dos piedras en sus caídas. Si nos fijamos medio segundo después de haber soltado las piedras veríamos (figura 14(b)) que están en las posiciones C y D, respectivamente. Nos damos cuenta de que la distancia entre los puntos C y D también es muy pequeña (de hecho es igual a la de los puntos iniciales A y B). En consecuencia, si la diferencia de condiciones iniciales es muy pequeña, entonces al transcurrir el tiempo la diferencia entre las posiciones de las dos piedras sigue siendo muy pequeña. Es decir, en este caso, las trayectorias que siguen son muy cercanas.

Veamos ahora otra situación. Supongamos que soltamos las dos piedras iguales desde puntos cercanos a la cima de una montaña (figura 15). La primera en la cima C, y la otra desde el punto A de la figura, es decir, un lugar que no es ya la cima, pero muy cercano a ella. ¿Qué ocurre ahora con las trayectorias de las piedras? Pues la primera se quedará en la cima mientras que la segunda rodará por la ladera de la montaña. En consecuencia, después de cierto intervalo, digamos 3 segundos, la separación entre las posiciones de ambas piedras será muy grande: una en la cima y la otra abajo. En este caso, nuevamente las condiciones iniciales de las dos piedras son muy parecidas pero ahora sus posiciones, al transcurrir el tiempo, difieren marcadamente. Es decir, con el paso temporal en este caso no se conservan las posiciones muy cercanas unas de otras.

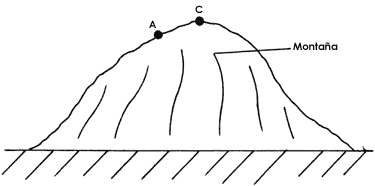
Figura 15. Dos piedras que caen desde puntos distintos de una montaña y a partir de posiciones muy cercanas, se separan mucho a lo largo de sus trayectorias.

Otro ejemplo se ilustra en la figura 16, en que se observa dos bolas de billar que inciden sobre una mesa que tiene varios botadores fijos. Las posiciones iniciales de las bolas son ligeramente distintas. Vemos que aun cuando las velocidades iniciales de las bolas sean las mismas, las trayectorias que siguen son completamente diferentes.

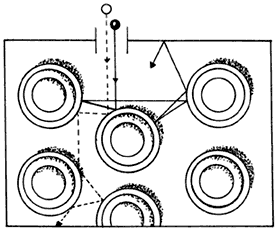
Figura 16. Ilustración de que variaciones pequeñas en las posiciones iniciales producen trayectorias muy separadas.

De los casos que hemos considerado podemos afirmar que hay dos tipos de situaciones: 1) Condiciones iniciales muy parecidas producen condiciones finales también muy parecidas, y 2) condiciones iniciales muy parecidas producen condiciones finales completamente diferentes.

Ahora bien, para determinar la evolución de un sistema cuando el tiempo transcurre debemos conocer las leyes que lo rigen, así como sus condiciones iniciales. Si fuera posible determinar con TODA precisión estas condiciones iniciales entonces podríamos saber en cualquier instante las características que tiene el sistema. A esto se refería Laplace (véase capítulo IV) cuando decía que si se le daban las condiciones iniciales del Universo podría determinar el futuro.

Sin embargo, en una situación real no podemos afirmar que se puedan determinar con TODA precisión las condiciones iniciales. Al medir estas cantidades siempre se cometerán errores, que son inevitables. Por lo tanto, lo más que se puede hacer es dar las condiciones iniciales en forma aproximada. Estas condiciones iniciales diferirán de las verdaderas condiciones iniciales del sistema en muy poco si los errores cometidos son pequeños. ¿Qué podemos decir acerca de la trayectoria que seguirá el sistema?, ¿podemos predecirla?

De lo que se ha visto puede ocurrir una de dos posibilidades: 1) Si estamos en un caso en que diferencias de condiciones iniciales producen condiciones finales muy parecidas, entonces podremos predecir qué ocurre con el sistema, con el transcurso del tiempo, también con un error pequeño. En este caso la separación entre las trayectorias es muy pequeña y la predicción que se haga será muy parecida a la trayectoria real. 2) Si se está en el caso en que pequeñas diferencias en las condiciones iniciales producen condiciones finales muy distintas, entonces la trayectoria real que siga el sistema se separará muy marcadamente de la trayectoria que podamos predecir. En este caso nuestra predicción está muy lejos de la realidad, por lo que no hay posibilidad de hacer predicción válida alguna.

En la cita de Poincaré mencionada en el capítulo IV, este científico se refirió precisamente a estas dos posibles situaciones. En el próximo capítulo se considerarán las consecuencias de estas posibilidades.

Los casos de las figuras 15 y 16 son ejemplos físicos de dependencia muy sensible de las condiciones iniciales.