VII. N�MERO Y NATURALEZA: LA DANZA DE PIT�GORAS
A PESAR de ser el lenguaje universal de la ciencia y el objetivo final de m�ltiples teor�as cient�ficas, el status de la matem�tica en tanto disciplina del saber humano es notoriamente borroso. �Qu� es, espec�ficamente, la matem�tica? Thomas Tymoczko del Smith College nos lleva a un tour por los extra�os bucles de esta cuesti�n. Para empezar veamos algunas respuestas curiosas.
Para Friederich Ludwig Frege (1848-1925), el fundador de la l�gica matem�tica y de la teor�a del significado modernas, la matem�tica es un tipo de metaf�sica, la ciencia m�s general de la realidad que incesantemente busca "las leyes de las leyes naturales". En este mismo sentido podemos afirmar hoy en d�a que en efecto las matem�ticas forman una especie de andamiaje metaf�sico del edificio cient�fico. Por su parte, Rudolf Carnap (1891-1970), el destacado fil�sofo del C�rculo de Viena y del positivismo l�gico, consideraba las matem�ticas como un tipo de lenguaje que busca las consecuencias anal�ticas de ciertas convenciones ling��sticas. Ciertamente, la matem�tica es un tipo de lenguaje, el m�s abstracto de ellos, con el que se expresan cierto tipo de relaciones mediante signos convencionales. Sin embargo se antoja que es algo m�s que un lenguaje, o bien, que si aceptamos que es un lenguaje, no se nos aclara con ello m�s que su l�xico. Poco podemos decir de cu�l es el significado de los signos y las operaciones. Para otro de los matem�ticos m�s formidables del siglo, Kurt Godel (1906-1978), el mismo que demostrara con el famoso teorema de la incompletud la imposibilidad de probar o falsificar las proposiciones matem�ticas a partir de sus axiomas fundamentales, la matem�tica es un tipo de psicolog�a introspectiva que informa de ciertas construcciones del pensamiento o la imaginaci�n, o mejor a�n, un tipo de geograf�a interior que busca precisar ciertos mapas del paisaje mental. Por m�s que nos pueda sorprender esta declaraci�n, no podemos dejar de reconocer que las leyes matem�ticas emanan de operaciones cognitivas necesariamente restringidas o moduladas por el aparato mental. Este mismo tipo de pensamiento late en el fondo de la filosof�a racionalista que supone que el Conocimiento surge de la propia mente m�s que de los objetos del mundo. No en vano varios de los mayores fil�sofos racionalistas como Descartes o Leibniz fueron matem�ticos.
Ahora bien, en el lado opuesto nos encontramos al empirista John Stuart Mill (1806-1873), para quien la matem�tica es una ciencia natural, de hecho la ciencia m�s inductiva que existe. Para los empiristas primero son los objetos, digamos los dedos, y de su percepci�n se derivan los conocimientos, digamos los n�meros y sus operaciones. Es curioso que esta idea, que se nos antoja del mayor sentido com�n, sea la que menos aceptaci�n tenga en los c�rculos matem�ticos y de filosof�a de la ciencia y haya sido refutada de manera contundente por Frege. El argumento que plantea es de una di�fana brillantez. Dice que si la matem�tica es emp�rica, entonces debe estudiar objetos reales, incluidos los procesos y los eventos. Por lo tanto, los objetos que estudia la matem�tica ser�an reales y no imaginarios o abstractos. En este punto el empirista se ve obligado a admitir aquello de lo que abjura: el n�mero, la funci�n, el logaritmo o la integral ser�an reales y no abstractos; de hecho, tan reales como las manzanas y los �tomos. Pero como no hay n�meros puros observables en el mundo habr�a que pensar en ellos como arquetipos de Plat�n, es decir, como objetos existentes en realidad, aunque en un plano ideal o trascendental donde fungen como templetes o modelos.
El asunto es tan anudado que alg�n pensador ha dicho que los matem�ticos pueden disfrutar de los beneficios del platonismo sin tomar las responsabilidades. En otras palabras, los matem�ticos pueden hablar como si sus entidades abstractas existieran, �pero sin realmente creer en ellas! La matem�tica ser�a as� una especie de mitolog�a, en la que usamos los mitos para entender ciertas realidades, explicar ciertos fen�menos o fundamentar los valores �ticos, pero no creemos que Zeus o Edipo existan "en realidad". Sin embargo esto no explica por qu� todos estamos de acuerdo en las pruebas matem�ticas ni por qu� no tenemos la misma actitud de referirnos a los �tomos o las manzanas como si existieran pero sin realmente creerlo.
William Quine (nacido en 1908), el famoso l�gico de Harvard y uno de los padres de la llamada filosof�a anal�tica, argument� que la matem�tica es un universo continuo y no separado del de la ciencia y que ambas eran necesarias para justificar nuestra experiencia. El n�mero y el �tomo son postulados cuya existencia se justifica plenamente por el papel que desempe�an en explicarnos las cosas. Seg�n esto, las matem�ticas no son completamente emp�ricas, o sea, que no est�n totalmente ancladas a la realidad, pero tampoco son pura geograf�a mental, sino que flotan en el limbo entre ambos mundos. Resumiendo: son casi emp�ricas."
Pong�moslo en t�rminos del matem�tico ingl�s Roger Penrose: �son las matem�ticas invenci�n o descubrimiento? Cuando los matem�ticos llegan a resultados en sus c�lculos, �producen s�lo construcciones mentales o encuentran, como se supone que hace la ciencia, realidades que estaban ah� listas para ser descubiertas? Es de notarse que si aceptamos la segunda opci�n, como lo hace Penrose sin ambages, de nuevo le estamos otorgando al n�mero un status de realidad concreta en el sentido del arquetipo plat�nico.
En este momento debe hacer su entrada al espect�culo la computadora. Despu�s de todo la computadora no es una persona, aunque hay quien argumenta lo contrario. En cualquier caso la computadora no tiene mente en el sentido humano del t�rmino y es, adem�s, un aditamento tecnol�gico como el �baco o el microscopio, pero un aditamento que habla (o mejor dicho que opera) con lenguaje matem�tico. En ese caso podemos hacer una pregunta determinante: adem�s de hacer operaciones matem�ticas, �puede la computadora probar o producir un teorema? La respuesta es afirmativa. La computadora puede probar teoremas, incluso complejos, pero la manera como lo hace no se parece a la forma, por ejemplo, como se prueba el teorema de Pit�goras, sino que se parece m�s a un experimento cient�fico cuyo resultado puede obtenerse si se reproducen ciertas condiciones. Conclusi�n: la computadora tampoco nos demuestra que la matem�tica sea netamente racional o emp�rica. Nos quedamos con la nebulosa soluci�n de Quine.
El punto fundamental que Tymoczko quiere demostrar es que los objetos abstractos existen y que pueden ser analizados cient�ficamente. M�s a�n, que los objetos del mundo son tambi�n abstractos. Recordemos que la diferencia entre lo concreto y lo abstracto es que lo primero ocurre en el espacio y el tiempo y lo �ltimo supuestamente no. Con los objetos concretos —pelotas, bosques, nubes, �tomos o manzanas— podemos interactuar, con los abstractos —n�meros, pensamientos, creencias— no. Ahora bien, si consideramos que todos los objetos son abstractos, nos vemos en la necesidad de aceptar que s�lo existe la mente o de que es lo �nico de lo que podemos estar seguros. De esto, que es idealismo puro, reniega la ciencia, aunque no faltar� alg�n neurocient�fico astuto que diga que, en efecto, la realidad es fabricada no precisamente por la mente sino por el cerebro, lo que viene a ser lo mismo. Todo lo que percibimos, pensamos, inferimos, incluido el lenguaje com�n y el matem�tico, es producto de la funci�n cerebral o la funci�n misma. Sin embargo, si queremos ser insidiosos, podremos agregar que tambi�n el cerebro es un objeto m�s de ese mundo de la mente.
En fin, quiz�s se pueda considerar al materialismo y al idealismo (o a sus parientes, el empirismo y el racionalismo) como puntos de vista complementarios, o que los objetos son a la vez concretos (es decir, que existen fuera de un observador) y abstractos (que su representaci�n mental es una construcci�n). Pero dentro de esta conciliadora soluci�n, �d�nde qued� el n�mero?
N�MERO, ARTE Y NATURALEZA: UNA RELACI�N EN SERIE
Bajo los tediosos c�lculos y manipulaciones de las matem�ticas yace un mundo de formas y pautas. Podemos comprobar esto en algunas secuencias de n�meros. Una de las secuencias m�s llamativas es la serie que present� Leonardo de Pisa, mejor conocido como Fibonacci (c. 1170-1250), al introducir el �lgebra en Italia despu�s de haber estudiado en el norte de �frica con un matem�tico �rabe. En su libro Liber abaci (1202) present� los n�meros indo-ar�bigos que se empezaban a conocer en Europa por la traducci�n al lat�n de Al-Kwarizimi y con los cuales Fibonacci afirmaba, acertadamente, que cualquier n�mero pod�a escribirse. En ese libro Fibonacci introdujo la secuencia que lleva su nombre.
Significativamente, la serie se origin� al resolver un problema biol�gico supuesto: �Cu�ntos pares de conejos se pueden producir a partir de un solo par, si cada par produce un nuevo par cada mes, s�lo los conejos de m�s de un mes de edad pueden reproducirse y ninguno se muere? Analicemos el problema: al principio hay un par de conejos, al mes sigue habiendo el mismo par, pero al segundo mes hay dos pares. Una de esas parejas puede reproducirse, pero la otra no, de tal forma que al tercer mes hay tres parejas. Dos de ellas se reproducen y a los cuatro meses hay cinco pares de conejos. Comprobemos c�mo va la secuencia de parejas: 1,1,2,3,5. Al analizar la serie nos damos cuenta de que no hay que continuar el c�lculo razonado porque la sucesi�n tiene una pauta num�rica recursiva: cada t�rmino o cifra de la misma es el resultado de sumar los dos t�rminos precedentes. A partir de entonces la secuencia 1,1,2,3,5,8,13,21,34,55,89... se llama serie de Fibonacci. El matem�tico franc�s E. A. Lucas introdujo, a fin del siglo pasado, la secuencia 2,1,3,4,7,11, 18... y otras similares que han recibido su nombre.
Los n�meros de Fibonacci y de Lucas son ejemplos perfectos de sucesiones recurrentes o conjuntos recursivos: aquellos que, a partir de dos elementos y gracias a una regla recursiva, echan a rodar una bola de nieve formada por un conjunto infinito de numeros. Este tipo de programas son inductivos y caracter�sticos del pensamiento l�gico. Douglas Hofstadter considera al par inicial (1, 1 para la serie de Fibonacci y 2,1 para la de Lucas) como el genotipo del cual surge el fenotipo, que es toda la secuencia, una ingeniosa analog�a del proceso mediante el cual un conjunto de genes (genotipo) origina una caracter�stica f�sica o conductual de los seres vivos (fenotipo). Pero la met�fora en este caso va m�s all� de la mera analog�a.
Aparte de m�ltiples y curiosas propiedades intr�nsecas, las series de Fibonacci tienen una notable relaci�n con formas artificiales y naturales. Robert Simpson de la Universidad de Glasgow not� ya en 1753 que en tanto los n�meros de la serie aumentaban en magnitud, la relaci�n entre dos t�rminos subsecuentes, es decir, la divisi�n del n�mero siguiente entre el anterior, se aproximaba a F (phi), la secci�n dorada o el n�mero de oro de los antiguos y cuyo valor es 1.6180. Esta misma cifra se hab�a obtenido originalmente al dividir un segmento cualquiera en dos porciones desiguales tales que la porci�n menor fuera a la mayor como �sta a todo el segmento. La relaci�n entre los dos segmentos es la secci�n �urea, que se encuentra frecuentemente en la geometr�a.
As�, el lado de un dec�gono regular es igual a la longitud del segmento m�s largo de su radio dividido en la secci�n dorada y el lado de un pent�gono regular tiene la proporci�n dorada respecto a la diagonal. Ciertamente la estrella de cinco puntas que se dibuja en el interior del pent�gono figura en los rosetones de las catedrales g�ticas y fue uno de los s�mbolos de la deidad. Adem�s, en un rect�ngulo "dorado" los lados tienen una relaci�n cercana a phi, es decir, una proporci�n de 5: 3, de 8: 5, de 13:8, etc. Los n�meros son, desde luego, vecinos en la serie de Fibonacci. Este rect�ngulo tiene las proporciones m�s agradables a la percepci�n, por lo que suele usarse para definir el tama�o de libros o cajas, adem�s de tener interesantes propiedades.
Por ejemplo, si al rect�ngulo dorado ABCD se le quita un cuadrado perfecto ABEF, el rect�ngulo remanente es tambi�n un rect�ngulo dorado al que se puede quitar un cuadrado, y as� sucesivamente. Si trazamos los arcos circulares se forma una espiral logar�tmica que se encuentra en la naturaleza y que fuera analizada geom�tricamente por Descartes como la curva de vectores radiales que se traza de un punto fijo (el centro de la espiral) bajo un �ngulo constante de 137.5.
Toda una est�tica pitag�rica se funda en el n�mero de oro. Tuvo una gran influencia sobre Leonardo da Vinci y Durero en sus empe�os para cuantificar y encontrar bases matem�ticas de dise�os pl�sticos y arquitect�nicos. El rect�ngulo dorado fue usado por el pintor impresionista George Seurat en m�ltiples cuadros, como La Parade (1888) y afirm� al respecto en una carta: "�ven poes�a en mi trabajo?. No: yo aplico mi m�todo, eso es todo." La proporci�n �urea fue usada tambi�n por el eminente arquitecto de origen suizo Le Corbusier (1887-1965) en su teor�a del modulador, la unidad arquitect�nica para obtener dimensiones arm�nicas y que estableci� como una proporci�n dorada de la estatura humana.
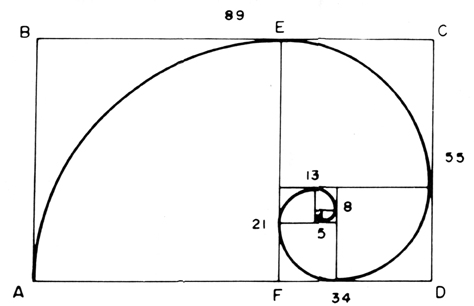
Figura 8. El rect�ngulo dorado.
Una correspondencia a�n m�s notable es el hecho de que los n�meros de la serie de Fibonacci y la espiral logar�tmica ocurran frecuentemente en la naturaleza. El ejemplo m�s notorio es la filotaxia espiral de ciertas plantas y se refiere a la ordenaci�n de sus hojas de manera helicoidal como consecuencia del desarrollo de las hojas que brotan una a una y crecen donde el espacio disponible entre ellas es mayor. La filotaxia se representa por una fracci�n en la cual el numerador es el n�mero de vueltas alrededor del tallo y el denominador el n�mero de hojas, ramas o espinas en ese recorrido. En todos los casos estos n�meros son t�rminos de las serie de Fibonacci. Adem�s, el n�mero de p�talos en las flores suele ser miembro de la serie: lila (3), ran�nculo (5), espuela (8), cal�ndula (13), aster (21) y varios tipos de margaritas (34, 55, 89). La espiral logar�tmica se encuentra, adem�s de las espirales de la filotaxia, en las conchas de los caracoles o los retorcidos cuernos de animales. Pero no s�lo en las formas de los seres vivos se han hallado series de Fibonacci: los astr�nomos se han percatado de que los eclipses tienen pautas de repetici�n cada 6, 41, 47, 88,135, 223 y 358 a�os, secuencia que corresponde a una serie de Lucas.
A pesar de que est�n muy bien establecidas las razones por las que ocurre la serie num�rica, la proporci�n �urea en arte y la filotaxia, sigue siendo un misterio la raz�n de su inquietante coincidencia. El poeta simbolista Paul Val�ry (1871-1945) ve�a en esto la raz�n de un dinamismo que representa el equilibrio entre el saber, el sentir y el poder. No en vano Val�ry era uno de esos raros esp�ritus que se encontraba como en su casa entre conocimientos filos�ficos, matem�ticos, arquitect�nicos o literarios de manera tal que, por ejemplo, estaba versado en el trabajo de los mayores f�sicos de su tiempo, como De Broglie, Einstein o Maxwell.
Como colof�n agregar� que, en forma por dem�s sugerente, Ghyka (citado en el Diccionario de los s�mbolos de Chevalier y Gheerbrant) consideraba la secci�n �urea el "s�mbolo abreviado de la forma viva, de la pulsi�n, del crecimiento".
He mencionado que los n�meros que llamamos ar�bigos se empezaron a usar en Europa despu�s de la obra de Fibonacci en el siglo XIII, varios siglos despu�s de que fueran introducidos al mundo isl�mico por Al-Kwarizimi quien, a su vez, los tom� de la India. Estos diez d�gitos singulares que corresponden a las unidades se han llamado n�meros naturales y han ejercido una poderosa fascinaci�n sobre los seres humanos a lo largo de la historia. Uno de los heraldos de tal fascinaci�n fue la tesis pitag�rica, seg�n la cual el propio cosmos, desde el movimiento de los planetas hasta la estructura de la m�sica, responde a un arreglo num�rico. Otro ejemplo es la producci�n de cuadrados "m�gicos", como aquel famoso reproducido en un cuadro de Durero y que dan el mismo resultado si se suman cualquiera de sus columnas o renglones.
Probablemente en la base de esta fascinaci�n se encuentre el m�ltiple y rec�ndito simbolismo de los n�meros. Es as� que la unidad, la dualidad, la trinidad, los puntos cardinales o los planetas visibles, han sido tomados como significados del 1, el 2, el 3, el 4 y el 7, respectivamente. En este marco y debido a que el n�mero 9 es el �ltimo y el mayor de los d�gitos se le han adjudicado significados de plenitud, culminaci�n y t�rmino de ciclo en las m�s diversas culturas. En efecto, el s�mbolo de Our�boros, la serpiente que se muerde la cola, se relaciona gr�ficamente con la reproducci�n y con el n�mero nueve en varios alfabetos antiguos. Por similar raz�n, en la mitolog�a griega encontramos que existen nueve musas, de las cuales la novena es la del conocimiento. Significativamente, la filosofia neoplat�nica de Plotino fue vertida en la Eneida (los nueve libros) y lleg� a ser un ingrediente importante en el misticismo jud�o, cristiano e isl�mico. Componentes de ese misticismo son la identificaci�n de Beatriz y el n�mero nueve en Dante (Vita nuova 30, pp. 26-27), la referencia de Roger Bacon a la novena casa del hor�scopo como la de la divinidad y la sabidur�a, o el antiguo enanegrama popularizado en nuestro siglo por George Gurdjieff y Peter Ouspensky.
Una propiedad fundamental del nueve fue enunciada por Avicena de la siguiente manera: "todo n�mero, sea cual fuere, no es sino el n�mero nueve o su m�ltiplo m�s un excedente, pues los signos de los n�meros no tienen m�s que nueve caracteres." Debido a esta propiedad, es factible calcular el excedente o remanente de dividir entre nueve simplemente sumando los d�gitos que forman cualquier n�mero. As�, el n�mero 836 se reducir�a al 8 (8 + 3 + 6 = 17,1 + 7 = 8). En efecto, 836/9 = 92 y sobran 8. Por su parte, los m�ltiplos de 9 no tendr�an remanente y la suma de sus d�gitos es siempre igual a 9. Se puede producir un cuadrado "m�gico" sustituyendo con sus excedentes a los n�meros de una tabla pitag�rica de multiplicar, como se ilustra a continuaci�n:
El cuadrado resultante a la derecha, si eliminamos la columna y el rengl�n finales de los nueves, tiene propiedades curiosas que dan lugar a formas m�ltiples. Entre las propiedades podemos mencionar que contiene varios ejes de simetr�a, que la suma de sus columnas o hileras, reducida a un d�gito, siempre da el n�mero nueve, y que las figuras que trazan los dise�os geom�tricos de unir n�meros 1,2,3,4 y 5 son espejos de los n�meros 8,7,6,5 y 4, respectivamente. Estos pares (1,8; 2,7; 3,6 y 4,5) son "complementarios" en el sentido de que suman nueve. Los dise�os que resultan de la uni�n de los n�meros son figuras geom�tricas que decoran buena parte del arte isl�mico. Adem�s, el cuadrado recuerda un tablero de ajedrez donde los n�meros 4 o 5 marcan los movimientos del caballo, los m�ltiplos del 3 los de la torre, los 2 y 7 a los alfiles. Notemos tambi�n que el n�mero cabal�stico 142857 puede definirse como una serie de complementarios situados cada tercera posici�n excluyendo los m�ltiplos de 3.
El escultor Juan Luis D�az ha analizado este cuadrado extensamente y lo ha usado para recrear las formas que resultan de la uni�n de los d�gitos, sean los mismos o diferentes. Adem�s, si se piensa que la tabla es una de las caras de un cubo m�gico, la uni�n de sus n�meros interiores conforma estructuras geom�tricas tridimensionales que recuerdan a los cristales naturales. D�az ha presentado una amplia exposici�n de estas estructuras en 1990 en Par�s.
Ahora bien, adem�s de estas estructuras, el residuo de nueve puede revelar otras muy distintas. Tomemos la serie de Fibonacci cuyos n�meros, como hemos visto, se forman al sumar los dos anteriores de la manera 1,1,2,3,5,8,13,21,34,55,89, 144... y que tienen una relaci�n directa con la secci�n y la espiral "doradas", las cuales se han usado en el arte y encontrado en la naturaleza. Pues bien, si reducimos a un d�gito la serie de Fibonacci nos encontramos con la siguiente serie de n�meros: 1,1,2,3,5,8,4,3,7,1,8,9,8,8,7,6,4,1,5,6,2,8,1,9,1,1,2...
A primera vista la serie podr�a parecer azarosa, pero nada m�s lejos de la realidad. Por ejemplo, la serie se repite cada 24 n�meros, tiene un nueve en la doceava y la veinticuatroava posici�n, en tanto que cada cuarto d�gito es m�ltiplo de tres. Despu�s de cada nueve viene un d�gito repetido, que es el complementario del que sigue al pr�ximo nueve. De hecho, la serie se divide en dos series de 12 n�meros en posiciones complementarias, y tomando al doceavo nueve como centro hacia los lados se alternan n�meros id�nticos y complementarios. Adem�s de �sta, existen otras dos series de Fibonacci reducidas de secuencias diferentes, pero de propiedades id�nticas. Veamos las tres superpuestas y comparemos las propiedades enunciadas:
| 1, l,2,3,5,8,4,3,7, 1,8,9,8,8,7,6,4,l,5,6,2,8,1,9 |
| 2,2,4,6, l,7,8,6,5,2,7,9,7,7,5,3,8,2,1,3,4,7,2,9 |
| 4,4,8,3,2,5,7,3,1,4,5,9,5,5,1,6,7,4,2,6,8,5,4,9 |
Las tres series tienen las propiedades antes descritas y son notoriamente arm�nicas, r�tmicas y recurrentes. Es notable encontrar que los d�gitos de todas las posiciones, exceptuando la cuarta, octava, doceava, etc., son miembros del numero m�gico" 142857, cuyo remanente es, por cierto, el 9; y c�mo lo son tambi�n los remanentes de todos los n�meros primos, aquellos que s�lo son divisibles entre s� mismos y entre uno. Alguna vez comprob� con dos amigos m�sicos —Tom�s Kalmar y John Bailis— que si se les asignan notas musicales a los d�gitos de las series y se toca la melod�a resultante, �sta es particularmente agradable y recuerda a ciertas partituras barrocas.
El por qu� las series recurren cada 24 o cada 12 posiciones tiene que ver con el propio mecanismo generador de la serie, es decir, con su genotipo: el hecho de que dos cifras seguidas que se suman para obtener la siguiente produzcan necesariamente una secuencia que da un ritmo cada cuatro posiciones y otro menos aparente cada tres. De todas estas cifras, 12 es el m�ltiplo com�n.
Ahora bien, as� como las series de Fibonacci tienen equivalentes naturales o culturales, podr�a esperarse que estas series las tuvieran tambi�n. En efecto, la ciclicidad de las series recuerda de inmediato la divisi�n del d�a en un ciclo de 24 horas y dos de 12. Esta divisi�n aparentemente arbitraria del d�a es una herencia del sistema duodecimal que usaban babilonios y sumerios, como lo es tambi�n la afici�n de contar por gruesas, que son 12 docenas de objetos (144, el doceavo t�rmino de la serie = 1 + 4 + 4 = 9), la divisi�n del pie en 12 pulgadas y la creencia de que el n�mero 13 es de mala suerte. El sistema duodecimal ha influido en el simbolismo de la cultura greco-mediterr�nea extensa y profundamente; algunas pruebas: son 12 los signos del zodiaco, son 12 las tribus de Israel, 12 los disc�pulos de Cristo y 12 los meses del a�o. En general se puede decir que el 12 tiene ventajas sobre el 10 como sistema de c�lculo debido a sus m�ltiples divisores. Ahora podemos ver que tiene, adem�s, otras propiedades secuenciales y reverberantes que son intr�nsecas a las series num�ricas de Fibonacci.
Se dice que hoy d�a es posible derivar la totalidad de las matem�ticas conocidas de una sola fuente: la teor�a de los conjuntos. Esto no es extra�o, ya que la noci�n de conjunto es quiz�s m�s antigua y cognoscitivamente m�s elemental que la de n�mero. Por ejemplo, supongamos que un grupo de humanos primitivos que no supieran contar m�s all� de lo quisieran elegir como l�der al hombre que poseyera m�s cabras. Pasando los reba�os de los candidatos de par en par por una puerta podr�an determinar cu�l es el reba�o m�s numeroso sin necesidad de contar.
La correspondencia 1 a 1 entre dos colecciones o conjuntos de objetos fue precisamente el tema inicial de estudio de Georg Cantor (1845-1918), matem�tico alem�n de origen dan�s, que desemboc� en la formulaci�n inicial de la teor�a de los conjuntos. Cantor defini� a un conjunto como la colecci�n en un todo de objetos distintos y definidos a nuestra percepci�n o pensamiento, objetos que se llaman elementos del conjunto. Los n�meros naturales forman, as�, un conjunto infinito; los n�meros pares o los de Fibonnacci, subconjuntos del anterior. En caso de existir dos o m�s conjuntos se dice que la uni�n de ellos es el conjunto que contiene a todos los elementos de los originales y la intersecci�n incluye a los elementos que son comunes a los originales. Estas nociones se representan usualmente con c�rculos, cada uno de los cuales constituye un conjunto.
As�, la intersecci�n es el �rea de traslape entre dos o m�s c�rculos superpuestos. El diagrama m�s conocido consta de tres c�rculos y se puede generar si en cada v�rtice de un tri�ngulo equil�tero, tomado como centro, trazamos tres c�rculos que unan a los otros dos v�rtices. Se forman as� ocho �reas, tres correspondientes a la zona exclusiva de cada c�rculo, tres a las intersecciones de dos c�rculos, la zona central que es la intersecci�n de los tres y la totalidad o uni�n de todos. Esta misma figura se conoce en geometr�a como tri�ngulo de Rouleaux.
El diagrama de tres c�rculos superpuestos manifiesta de una manera inmediata e intuitiva las propiedades fundamentales de los conjuntos; constituye, adem�s, un antiguo s�mbolo con m�ltiples significados y usos. El diagrama fue popularizado por John Venn, un l�gico ingl�s, para reducir la l�gica y la teor�a de los conjuntos al c�lculo simb�lico puro. Venn utiliz� el diagrama para identificar los silogismos fundamentales que se usan en la l�gica. La extensi�n de cada uno de los tres t�rminos del silogismo se representa por uno de los c�rculos, de tal manera que las �reas de intersecci�n pueden resultar claramente eliminadas por identidad l�gica y cada una de las formas silog�sticas tiene un diagrama peculiar. Al llevar esta ruta m�s lejos se ha propuesto que la sem�ntica se puede definir como una rama de la teor�a de los conjuntos que se aboca a la naturaleza y las relaciones de los agregados del lenguaje, en tanto que la sintaxis ser�a una rama de la teor�a de los n�meros.
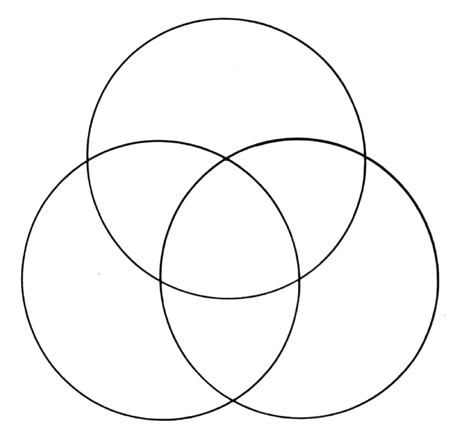
Figura 9. Tri�ngulo de Rouleaux o diagrama de Venn.
Independientemente de estos esfuerzos parece interesante constatar que se ha usado el tri�ngulo de Rouleaux o el diagrama de Venn en la teor�a de los colores. As�, si cada uno de los tres c�rculos se llena de luz verde, roja y azul obtenemos la mezcla aditiva de tal manera que la intersecci�n del verde y el rojo es de color amarillo, la mezcla del rojo y azul es magenta, y la de azul y verde es cian. Desde luego, la intersecci�n central de los tres colores es blanca. Esto sucede cuando se mezclan las luces de los tres colores, en tanto que la mezcla de pigmentos produce mezclas que se llaman sustractivas, ya que involucran la absorci�n de la luz que incide sobre los pigmentos y la transmisi�n de su resta al ojo.
Toda la gama de colores que percibimos se puede obtener por la mezcla de los tres fundamentales, un hecho establecido por primera vez por el fisi�logo Hermann von Helmholtz en 1850. La base biol�gica de esto se encuentra en el dato de que nuestra retina tiene tres tipos de c�lulas receptoras a la luz que son �ptimamente sensibles a longitudes de onda de 445 nan�metros, correspondiente al azul, 535 que equivalen al verde y 565 al rojo. Es decir, se puede concebir la visi�n en color con la idea de tres conjuntos de receptores que son estimulados en diferente grado por la luz. El mismo principio, desde luego, ha sido aplicado para el desarrollo de la televisi�n a color.
Podr�a proponerse que el diagrama de Venn subyace tambi�n en muchas operaciones metodol�gicas y cognoscitivas que realizan los cient�ficos y los eruditos. Por ejemplo, uno de los criterios de veracidad en la ciencia de la historia consiste en la comparaci�n de las fuentes en busca de intersecciones. Cuando se detecta informaci�n similar en varias fuentes hist�ricas se considera que los hechos tienen mayor probabilidad de haber ocurrido. En el mismo sentido se han generado algunas ideas sobre mecanismos psicol�gicos o posiciones filos�ficas. Por ejemplo, la coincidencia —o si se quiere, la intersecci�n— de temas comunes o aun id�nticos en mitolog�as antiguas y que puede interpretarse como el resultado de comunicaci�n entre las culturas se toma, m�s parsimoniosamente, y con base en la teor�a de los conjuntos, como la manifestaci�n de propiedades inconscientes comunes a la mente humana, como podr�an ser, por ejemplo, los arquetipos de Jung. En un sentido af�n, el notable pensador y novelista Aldous Huxley escribi� un ensayo profusamente documentado del pensamiento m�stico en m�ltiples personalidades de culturas separadas ampliamente en el espacio y el tiempo en busca precisamente de los elementos comunes a los que, una vez identificados, denomin� La filosof�a perenne.
Muchos diagramas simb�licos, como el mandala, se antojan cristalizaciones de capacidades y operaciones cognitivas cinceladas en nuestra biolog�a. De esta forma, no es sorprendente comprobar que el diagrama de Venn es un s�mbolo que ha aparecido repetidamente en el pasado. Por ejemplo, lo he encontrado en un escudo de armas medieval que se exhibe en el Museo de Artes Regionales de la antigua ciudad de Lugo, Espa�a. Al indagar sobre el posible significado del dibujo me top�, en el Diccionario de los s�mbolos de Chevalier y Gheerbrandt, con un diagrama usado en el siglo XII como s�mbolo de la Trinidad en una miniatura que se conserva en la catedral de Chartres. Cada uno de los c�rculos representa all� a una de las tres personas de la Trinidad, en tanto que la intersecci�n est� ocupada por la palabra "unidad". Evidentemente, nuestro diagrama ayud� a los te�logos medievales a entender el dogma contradictorio de "tres personas distintas y un solo Dios verdadero".
En la historia del conocimiento recurren las mismas met�foras. Agreguemos una m�s: ciencia, arte y sabidur�a pueden concebirse como conjuntos que se intersectan. La uni�n de �stos es el conocimiento en su sentido m�s general, en tanto que su intersecci�n —la unidad de los tres tipos de conocimiento— corresponder�a a la filosof�a.
A juzgar por la convergencia de la ciencia y el arte en la matem�tica musical, el sue�o de una s�ntesis de la ciencia y las artes parece empezar a hacerse realidad. Entre los antecedentes de esta interdisciplina cabe recordar que en el siglo pasado el f�sico alem�n Ernst Chladni (1756-1827) encontr� que la aplicaci�n de un arco de viol�n a un plato de vidrio espolvoreado con arena produce una vibraci�n que reacomoda la arena en formas sim�tricas y espectaculares que deslumbraron a Napole�n. Chladni calcul� la velocidad del sonido en diferentes gases y con esos datos construy� un instrumento musical, el eufonio, que deber�a figurar como un antecedente en el juego de los abalorios. En 1967 Hans Jenny desarroll� la t�cnica de Chladni para visualizar notas musicales: una l�mina de metal colocada horizontalmente y espolvoreada uniformemente con arena. En el centro de la cara inferior de la l�mina se aplica una vibraci�n f�sica determinada por una nota musical espec�fica. La vibraci�n de la l�mina se traduce en un arreglo de la arena en bellas formas conc�ntricas susceptibles de un an�lisis matem�tico que sintetizan las propiedades visuales y geom�tricas de las notas musicales.
En el momento actual la computadora se ha constituido en un instrumento tanto anal�tico como interpretativo y creativo en el �mbito de la matem�tica musical. He aqu� algunos ejemplos reunidos en el semanario de publicaciones cient�ficas Current Contents del 4 de noviembre de 1991. Es posible que el an�lisis matem�tico de la m�sica permita la producci�n de obras similares a las composiciones cl�sicas. En efecto, Kenneth J. Hsu, un profesor de geolog�a del Instituto Federal de Tecnolog�a en Zurich y su hijo Andrew han propuesto que la matematizaci�n de las obras de Bach en forma de matrices puede conducir a nuevas construcciones musicales indistinguibles de las obras conocidas de Bach. Mediante el uso de un instrumento electr�nico llamado caja fractal de m�sica, los Hsu reducen una composici�n a su forma fundamental usando la teor�a de los fractales. Se produce as� una suerte de resumen de los temas que puede ser utilizado para concebir temas similares. Los Hsu encontraron en la m�sica de Bach y de Mozart que los intervalos de frecuencia o los cambios de frecuencia ac�stica tienen una geometr�a fractal.
Para entender las propiedades fractales de la m�sica conviene empezar diciendo que la m�sica es un sonido estoc�stico, es decir, una secuencia de notas que no es totalmente azarosa, lo cual ser�a ruido, ni totalmente mon�tona, lo cual ser�a aburrido. La m�sica que nos interesa tiene una estructura mel�dica suficientemente previsible para resultar placentera, de tal manera que muchas veces podemos adivinar el desarrollo de una melod�a antes de haberla escuchado, s�lo por la estructura de la parte que ya o�mos. Pero tambi�n nos interesa que, dentro del contexto de la estructura previsible, surja una novedad af�n a ella, lo cual renueva nuestra atenci�n y estimula el inter�s.
La geometr�a fractal se adapta a la naturaleza de manera mucho m�s precisa que la geometr�a euclidiana cl�sica. Es as� que las nubes no son esferas, que las costas no son c�rculos o que los rel�mpagos no son l�neas. Sin embargo, ninguno de ellos es amorfo; su forma es mas compleja y puede ser descrita mejor con esta nueva geometr�a. De acuerdo con el di�fano ejemplo de Benoit Mandelbrot, el fundador de la teor�a de los fractales, si medimos la longitud de un terreno con una vara obtenemos un resultado de X n�mero de varas. Si repetimos el procedimiento con varas cada vez m�s cortas, el n�mero de varas ser� cada vez mayor y, en el caso de terrenos te�ricamente planos y lisos, el n�mero de varas peque�as siempre ser� m�ltiplo de las varas mayores. Ahora bien, si el terreno es accidentado, el n�mero de varas chicas exceder� al de las grandes en proporci�n mayor a su diferencia de tama�o, porque aqu�llas medir�n m�s detalles del terreno que �stas. La relaci�n matem�tica entre estos n�meros, que suele tener constancias en las formas naturales, es el campo de la geometr�a de los fractales. Es en este sentido que los Hsu encontraron que las frecuencias y tiempos de la m�sica de Bach y de Mozart se ajustan a la teor�a.
Ahora bien, pensemos que la ejecuci�n de una obra musical se compone de dos partes: una partitura, que es una secuencia predeterminada de notas fijada por el compositor, y los factores expresivos, como el tempo o las sutiles modificaciones en duraci�n y volumen que controla el ejecutante o el director. Son precisamente estos �ltimos la parte fundamental del entrenamiento musical, ya que el aprendizaje del lenguaje musical de las partituras es mucho m�s f�cil que las horas interminables de penitencia que constituyen los tediosos ejercicios a los que debe someterse el futuro concertista para desarrollar el virtuosismo necesario para ejecutar la obra de una manera precisa y creativa. Hasta hace poco, con los sintetizadores y las computadoras era posible solamente imitar la partitura pero no los factores expresivos.
Pues bien, Max Mathews, del Departamento de M�sica de la Universidad de Stanford, ha descrito un sistema de c�mputo que le da a la persona control creativo sobre la ejecuci�n sin necesidad de perfeccionar su t�cnica. El sistema es lo suficientemente adecuado como para producir m�sica de calidad igual a la de un ejecutante entrenado, al menos para los o�dos no educados.
Estos descubrimientos implican que el factor m�s sutil de la producci�n conductual que se manifiesta en la m�sica, es decir, la cualidad, es factible de ser analizado y reproducido. En efecto, Manfred Clynes, m�sico y neurocient�fico, ha afirmado que las emociones expresadas en la m�sica tienen forma y que se puede analizar esa forma con una m�quina relativamente simple inventada por �l que mide las presiones de los dedos en la ejecuci�n de un instrumento. Esto es muy interesante ya que es bien sabido que, a excepci�n del entrenamiento de la voz, la mayor�a de los instrumentos musicales se tocan mediante el aprendizaje de una serie de patrones fundamentales de disposiciones de los dedos llamados digitaciones y que la emoci�n de la ejecuci�n (el factor expresivo) se trasmite mediante sutiles diferencias en la vibraci�n, la presi�n y la duraci�n de las digitaciones. Manfred Clynes descubri� algunos par�metros matem�ticos de esos pulsos y con ellos program� una computadora para manipular frases, amplitudes y pausas, con lo cual ha empezado a producir expresiones musicales emocionales en la m�quina.
El problema remanente de este enfoque es que reduce la expresi�n musical a
la digitaci�n, cuando los ejecutantes avanzados saben que hay un elemento holista
en el movimiento que expresa el ejecutante. Dice Yehudi Menuhin:
la mera colocaci�n
del dedo, incluyendo el vibrato, cambios de posici�n y el glissando
son todos aspectos del mismo movimiento b�sico. Todo el cuerpo debe
estar involucrado sin ofrecer resistencia en parte alguna, s�lo soporte.
El objeto del entrenamiento est� en el continuo estado de balance, en
el equilibrio de todas las partes. |
En cualquier caso el avance de la matem�tica musical es espectacular y la computadora se acerca al juego de los abalorios de Hermann Hesse.
Alem, J.-P. (1988), Juegos de ingenio y entretenimiento matem�tico, Gedisa, Barcelona.
Dalmedico, A. D. (1991), "Sophie Germain", Scientific American 265 (6), pp. 76-81.
Chevalier, J., Gheerbrandt, A. (1988), Diccionario de los s�mbolos, Herder, Barcelona.
Gardner, M. (1987), Los m�gicos n�meros del doctor Matrix, Gedisa, Barcelona.
Mandelbrot, B. (1990), "Monta�as y dragones fractales: la intuici�n en la matem�tica y en las ciencias", en: Sobre la imaginaci�n cient�fica (Wagensberg, J., comp.) Tusquets, Barcelona.
National Council of Teachers of Mathematics (1987), El sistema de los n�meros racionales, Trillas, M�xico.
Rainwater, C. (1971), Light and Color, Golden Science Guide, Nueva York.
Schimmel, A. (1993), The Mystery of Numbers, Oxford University Press, Nueva York.
Tymoczko, T. (1991), "Mathematics, Science and Ontology", Synthese 88, pp. 201-228.
![[Inicio]](../img/begin.gif)
![[Anterior]](../img/prevsec.gif)
![[Siguiente]](../img/nextsec.gif)