I.2. PLAT�N Y ARIST�TELES

Arist�teles fue el primero en se�alar que el estudio de las causas de los fen�menos se hab�a iniciado con Tales de Mileto, de quien se sabe que estaba vivo en el a�o 585 a.C. El fen�meno general que Tales y otros fil�sofos presocr�ticos intentaban explicar era la existencia del cambio continuo en las apariencias frente a la preservaci�n de la naturaleza; para ello propusieron que el mundo est� formado por un sustrato invariante que adopta diferentes formas. Tales dijo que ese sustrato era el agua, Anax�menes que era el aire, Anaximandro que era el apeiron o �ter. En cambio, Plat�n invent� su teor�a de las ideas, entes universales, perfectas y con existencia verdadera (objetiva), de las que los hechos y objetos reales y materiales no son sino ejemplos imperfectos. Adem�s, Plat�n se�al� que cuando adquirimos nuevos conocimientos, lo que realmente hacemos es aumentar nuestra comprensi�n de esas ideas: no se trata de conocimientos incorporados por medio de nuestros �rganos de los sentidos (o sea, conocimientos de las apariencias), que Plat�n consideraba como enga�osos e ilusorios, sino de acercarse m�s al mundo de las ideas por medio del intelecto, donde quiera que ese mundo se encuentre.

Plat�n (430?-347 a.C.)

Para alcanzar el conocimiento, Plat�n mostr� varios procedimientos a lo largo de sus distintos di�logos. Por ejemplo, la f�rmula para comprender la idea de la belleza se encuentra en el Simposio, y consiste en empezar contemplando un objeto que todos consideren bello (el objeto que escogi� Plat�n como ejemplo de algo que todos en su sociedad consideraban bello es interesante: un esclavo jovencito y hermoso), despu�s se re�ne un grupo de tales jovencitos y se trata de identificar el patr�n com�n de su belleza, de ah� se pasa a examinar la belleza propia del proceso mismo de aprendizaje, despu�s la del aumento en el conocimiento, de ah� la de la generalidad de las leyes, y as� sucesivamente, hasta al final alcanzar la idea misma de la belleza. En cambio, en otro di�logo, el Menon, Plat�n (por medio de su representante S�crates) sugiere que el conocimiento de las ideas es realmente un reconocimiento, en vista de que ya las conoc�amos en alguna encarnaci�n anterior, o sea que se propone la existencia de ideas o conocimientos a priori. Naturalmente, me refiero a la famosa conversaci�n entre S�crates y el esclavo, en que el fil�sofo (despu�s de muchos trabajos) logra finalmente sacarle a su interlocutor un teorema matem�tico que nunca antes hab�a aprendido o escuchado, generando al mismo tiempo la palabra educaci�n, que viene del lat�n educare, que literalmente significa "sacar, extirpar".

Sin embargo, es en la Rep�blica donde Plat�n (siempre disfrazado de S�crates) presenta su concepto m�s desarrollado sobre la forma de ganar acceso al mundo de las ideas, y por lo tanto al conocimiento. Aqu� su interlocutor es Glauc�n, un hermano mayor de Plat�n y estudiante de filosof�a, con el que S�crates ensaya sus tres modelos cl�sicos, el sol, la l�nea y la cueva. Un breve resumen de los dos �ltimos nos servir� para examinar las diferencias entre el mundo sensible y el mundo inteligible, entre las meras opiniones y el conocimiento cient�fico y filos�fico, y entre los cuatro estados mentales designados por Plat�n como ilusi�n (eikasia), creencia (pistis), raz�n (dianoia) y pensamiento puro (episteme).

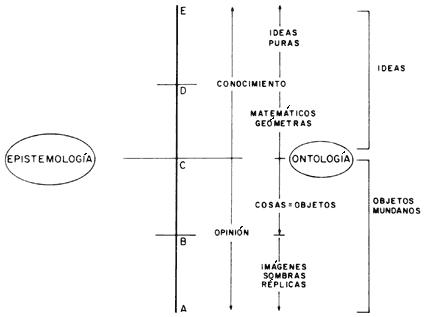
Las divisiones de la l�nea plat�nica

La l�nea vertical AE tiene una divisi�n mayor que la separa en dos mitades, AC y CE, cada una de ellas a su vez divididas en otras dos mitades: AC = AB + BC; CE = CD + DE. Pero la l�nea AE tambi�n separa dos compartimientos laterales, uno derecho (que es el lado ontol�gico) y otro izquierdo (que es el lado epistemol�gico). La divisi�n mayor de la l�nea AE separa, en el compartimiento derecho, un campo inferior (AC) que corresponde a la mera opini�n o doxa, y un campo superior (CE) que es el del conocimiento o episteme. El campo inferior AC est� a su vez formado por dos componentes, uno inferior (AB), constituido por im�genes o r�plicas de los objetos reales, en forma de sombras, modelos o im�genes, y otro superior (BC), que es el de los objetos mismos. El campo superior CE tambi�n est� integrado por dos espacios, uno inferior (CD) que corresponde al mundo de los matem�ticos y ge�metras, y otro superior (DE) en donde se encuentran las ideas. Para Plat�n, el �mbito del fil�sofo es el espacio DE, pero para alcanzarlo primero deben recorrerse las distancias AB, BC y CD: este �ltimo espacio (CD) siempre cont� con el inter�s especial de Plat�n, pero al mismo tiempo postul� que no se trataba de un mundo perfecto, en vista de que sus deducciones proven�an de postulados o axiomas primarios, o sea no justificados sino simplemente aceptados como verdades iniciales o incontestables. No importaba que los ge�metras hicieran modelos (casi) perfectos de sus teoremas, o que los matem�ticos presentaran pruebas (casi) inexpugnables de sus demostraciones; todas ellas estaban manchadas por el pecado original de la falta de justificaci�n racional de sus or�genes. Para pasar del espacio de los matem�ticos y ge�metras al mundo perfecto de las ideas (DE), Plat�n propuso un m�todo, la dial�ctica, que simplemente consiste en la discusi�n racional de la definici�n de un concepto entre individuos versados en el asunto, hasta que finalmente se llega a un consenso. Aunque esto puede decirse (y se ha dicho, sobre todo por Hegel) de varias maneras mucho m�s grandiosas y complicadas, en realidad eso es a lo que la dial�ctica se reduce en �ltima instancia.

El s�mil o modelo de la cueva es probablemente la alegor�a m�s famosa en toda la historia de la filosofía occidental. Plat�n la introdujo para ampliar sus conceptos sobre las distintas formas o etapas del conocimiento, que ya hab�a ilustrado con el esquema de la l�nea resumido arriba. Siempre por boca de S�crates, dialogando con Glauc�n, Plat�n describe su alegor�a de la cueva como sigue:

—Te invito a que ahora consideres la cultura o la ignorancia de nuestra condici�n humana m�s o menos de la manera siguiente. Imagina una c�mara subterr�nea como una cueva con una entrada ampliamente abierta a la luz del d�a y tan ancha como la misma cueva. En esta cueva viven prisioneros desde ni�os unos hombres, con las piernas y el cuello atados de tal forma que s�lo pueden mirar de frente y sin voltear a los lados. Detr�s, a cierta distancia y por arriba de ellos, arde una fogata, y entre el fuego y los prisioneros hay un camino elevado al que atraviesa una tapia, construida como las mamparas que los titiriteros colocan entre ellos y el p�blico y por encima de las cuales exhiben a sus mu�ecos.

—Ya veo.

—Imag�nate ahora que unos hombres transportan toda clase de utensilios por detr�s de la tapia, proyectando por encima de ella figuras de hombres y animales hechas de madera y piedra y de otros tipos de materiales; como podr�a esperarse, algunos de estos hombres estar�n hablando y otros no.

—Una imagen extra�a y un tipo extra�o de prisioneros.

—Son como nosotros —le dije— porque �piensas que ser�an capaces de ver alguna otra cosa aparte de las sombras proyectadas por el fuego en la pared de la caverna que tienen enfrente?

—�C�mo podr�an hacerlo si se les ha impedido que muevan la cabeza durante toda su vida?

—�Y podr�an ver algo m�s de los objetos que est�n siendo transportados por el camino?

—Naturalmente que no.

—Por lo tanto, si fueran capaces de hablar entre s�, �no supondr�an que las sombras que ven son las cosas reales?

—Inevitablemente.

El di�logo entre S�crates y Glauc�n contin�a con la descripci�n de lo que ocurre cuando uno de estos desdichados prisioneros se libera de sus cadenas y logra voltear la cabeza, mirar directamente a los cargadores y a sus objetos, contemplar el fuego, y hasta salir de la cueva y ver directamente la luz del sol. Pero ya no lo seguiremos en su viaje de liberaci�n, ni tampoco en su regreso a la profundidad de la cueva, porque Plat�n ya nos ha presentado el concepto relevante a nuestro inter�s en estas p�ginas. No cabe duda que la cueva corresponde al segmento AC de la l�nea, o sea al mundo visible en general, el de la mera opini�n (doxa), que posee un nivel inferior del conocimiento, caracterizado por Plat�n no como ignorante sino como inculto; en este segmento el hombre confunde a la realidad con sus sombras; en cambio, el mundo exterior, al que finalmente llega el prisionero que logr� evadirse de la cueva, es el equivalente al segmento CE de la l�nea, o sea el mundo del verdadero saber, del conocimiento pleno y absoluto, o sea el mundo de las ideas. En este �ltimo compartimiento se alcanza, seg�n Plat�n, la visi�n inteligible de la idea del bien.

En realidad, Plat�n ve�a con cierto desprecio el estudio de la realidad, de los fen�menos de la naturaleza. Lo que el fil�sofo deb�a hacer era intentar llegar al mundo de las ideas, en donde todo es perfecci�n absoluta. De acuerdo con Cornford, S�crates logr� cambiar el rumbo de la filosofía de sus predecesores y contempor�neos, que hasta su tiempo estuvo orientada al estudio y la comprensi�n de la naturaleza, por un inter�s primario en el individuo y en su alma. Como veremos a lo largo de estas p�ginas, el racionalismo y el subjetivismo son las dos caras de la misma moneda, acu�ada originalmente para la cultura occidental por Plat�n. Arist�teles, que fue su disc�pulo desde los 17 a�os de edad, inici� sus trabajos bajo la influencia de la teor�a de las ideas pero posteriormente se apart� de ella; incluso se ha dicho que buena parte de sus escritos tienen como objetivo combatir esa teor�a, aunque D�hring insiste en que Arist�teles nunca se libr� de la influencia de Plat�n. Arist�teles contribuy� de manera enorme a la teor�a del conocimiento, no s�lo por sus escritos sino por su influencia en los pensadores medievales, para quienes su opini�n sirvi� casi siempre de punto de partida y no pocas veces de �rbitro de la verdad. Para nuestro objetivo, conviene resumir las principales ideas aristot�licas sobre el m�todo cient�fico en las siguientes cuatro: 1) teor�a del silogismo; 2) teor�a de las definiciones; 3) el m�todo inductivo-deductivo; 4) teor�a de la causalidad.

1)Teor�a del silogismo. De acuerdo con Arist�teles, los mismos principios generales de razonamiento rigen en todas las ciencias, entre las que inclu�a la pol�tica, la �tica y la est�tica. Estos principios, que aparecen por primera vez en la Primera anal�tica, fueron inventados por Arist�teles y se refieren a las distintas formas que pueden tomar las proposiciones y las cu�les son v�lidas o inv�lidas. Como todos sabemos, los silogismos consisten de dos premisas y una conclusi�n, unidas en forma de inferencia o de implicaci�n; as�, el m�s famoso de todos los silogismos se puede expresar de las siguientes dos maneras:

Inferencia	Implicación
Todos los hombres son mortales.	Si todos los hombres son mortales.
Sócrates es un hombre.	y Sócrates es un hombre,
Por lo tanto, Sócrates es mortal.	entonces Sócrates es mortal.

�ste no es el sitio para repasar la compleja estructura de los diferentes silogismos, sino para se�alar que se trata de instrumentos poderosos para examinar el razonamiento cient�fico; no nos dicen nada, ni est�n dise�ados para hacerlo, sobre el contenido de verdad de las premisas, sino que se trata de simples reglas de l�gica para usarse una vez que las premisas se han alcanzado. Para esto �ltimo Arist�teles propuso su teor�a de las definiciones o de la esencia.

Arist�teles (384-322 a.C.), seg�n una representaci�n medieval del siglo XIII en la catedral de Chartres

2) Teor�a de las definiciones. En los T�picos, Arist�teles incluye su doctrina de las cinco formas como un predicado puede relacionarse con el sujeto, de las que dos son "convertibles", la definici�n o esencia y la propiedad; una no es "convertible", el accidente; y las otras dos son el g�nero y la especie. Lo mismo que Plat�n, Arist�teles pensaba que la m�s importante funci�n del fil�sofo era la b�squeda de las definiciones correctas de las cosas, o sean conceptos o universales. Esto requer�a, en primer lugar, la determinaci�n de su g�nero y de su especie, porque de ellos dependen las cualidades o atributos necesarios y suficientes para que algo sea una cosa del tipo o clase a la que pertenece, o sea que de ellos depende su esencia. Este aspecto de la filosof�a de Arist�teles es tan importante que algunos autores (como Popper) lo caracterizan como esencialismo, debido a que cuando conocemos la esencia de algo podemos deducir, a partir de ella, sus propiedades espec�ficas. Seg�n Arist�teles, una propiedad real de un objeto es algo que no revela su esencia pero que pertenece exclusivamente a ella y es convertible con ella; por ejemplo, Arist�teles dice que una propiedad del hombre es ser capaz de aprender gram�tica, porque si un ser vivo es un hombre, es capaz de aprender gram�tica, y si un organismo vivo es capaz de aprender gram�tica, es un hombre.

El esencialismo es interesante porque sugiere ya una posible estructura del m�todo cient�fico aristot�lico: basta establecer la esencia de los fen�menos que nos interesan y a partir de ella deducir sus propiedades, tal como se hace en geometr�a, en donde funciona muy bien. Por ejemplo, si definimos al c�rculo como una figura plana (�ste ser�a su g�nero) en donde todos los puntos de la figura son equidistantes a un punto fijo (�sta ser�a su especie), tal propiedad ser�a autom�ticarnente su esencia, que al mismo tiempo es convertible con el objeto, o sea el c�rculo. Pero el propio Arist�teles vio que este sistema no era satisfactorio en vista de que existen otros atributos de las cosas, los llamados accidentes, que no pueden derivarse de su esencia; por ejemplo, aunque la esencia del hombre es que es un animal racional (la definici�n es del propio Arist�teles) de ah� no puede derivarse si es alto, chaparro, flaco, gordo, bueno, malo, etc. De hecho, el descubrimiento de la esencia de las cosas no puede ser un proceso puramente l�gico y mental, sino que requiere tomarlas en cuenta, examinarlas y sujetarse a los resultados del examen. En sus propias palabras:

Debemos dirigir nuestra investigaci�n a la b�squeda de un grupo de cosas que sean semejantes en el sentido de ser espec�ficamente indiferentes, y preguntarnos qu� es lo que tienen en com�n; despu�s debemos hacer lo mismo con otro grupo dentro del mismo g�nero y perteneciente a la misma especie dentro del grupo, pero a otra especie distinta de la del primer conjunto. Una vez que hayamos descubierto para este segundo grupo qu� es lo que sus miembros tienen en com�n, y de manera semejante en varios otros grupos, debemos considerar de nuevo si las caracter�sticas comunes que hemos establecido tienen alg�n aspecto que es propio de todas las cosas examinadas, hasta que alcancemos una sola expresi�n. Esta ser� la definici�n requerida.

�sta es una de las primeras formulaciones de la inducci�n, o sea de la operaci�n l�gica que va de lo particular a lo general, que representa un salto hacia adelante en el conocimiento, un enriquecimiento repentino de la informaci�n derivada del examen de instancias particulares, un verdadero descubrimiento. Arist�teles est� postulando varias cosas al mismo tiempo, est� resolviendo a su manera una serie de problemas que volver�n a aparecer en la historia del pensamiento humano una y otra vez, y que todav�a hoy est�n con nosotros: en primer lugar, se�ala la participaci�n importante de las percepciones sensoriales en la recolecci�n de datos; en segundo lugar, supone que la mente tiene la capacidad de reconocer y aislar semejanzas entre objetos diferentes; en tercer lugar, que por medio de tales semejanzas se pueden construir clases distintas, como g�neros y especies. Pero sobre todo, Arist�teles est� proponiendo el m�todo cient�fico inductivo-deductivo.

3) El m�todo inductivo-deductivo. Arist�teles ilustra este m�todo por medio del an�lisis de un eclipse lunar: el cient�fico primero observa el oscurecimiento progresivo de la superficie lunar, y a partir de �sta y otras observaciones induce varios principios generales, que son que la luz viaja en l�nea recta, que los cuerpos opacos producen sombra, y que cierta situaci�n de dos cuerpos opacos cerca de un objeto luminoso resulta en que la sombra de uno de ellos se proyecta en el otro. De estos principios generales, y del hecho de que la Tierra y la Luna son cuerpos opacos, se deduce el mecanismo de producci�n del eclipse; en otras palabras, ha progresado del hecho de que la Luna se ha oscurecido a la comprensi�n del fen�meno.

De acuerdo con Arist�teles, los objetos individuales resultan de la uni�n de dos componentes: materia y forma. La materia les confiere especificidad individual mientras que la forma los hace miembros de una clase de objetos similares. Las generalizaciones acerca de la forma son las que se realizan por inducci�n, a partir de experiencias sensoriales. Arist�teles describe dos tipos de inducci�n, por enumeraci�n simple y por intuici�n: la primera es aquella en la que una serie de proposiciones sobre objetos o eventos se toma como base para una generalizaci�n acerca de la especie de que son miembros, raz�n por la cual las premisas y la conclusi�n contienen los mismos t�rminos descriptivos. Un ejemplo muy conocido es:

El cuervo 1 es negro

El cuervo 2 es negro

El cuervo 3 es negro

Todos los cuervos son negros

En cambio, la inducci�n intuitiva consiste en la apreciaci�n directa, muchas veces repentina, de lo que es esencial en un conjunto de datos sensoriales; el ejemplo que da Arist�teles es el de un observador que en varias ocasiones nota que el lado brillante de la Luna es el que mira hacia el Sol y de pronto se da cuenta de que la Luna brilla porque refleja la luz del Sol. Arist�teles se�ala que este tipo de intuici�n s�lo se desarrolla despu�s de una experiencia extensa, que los observadores experimentados ven con mayor penetraci�n, o son capaces de percibir m�s, en uno o un grupo de objetos o fen�menos, que los que apenas se inician en esas tareas.

A pesar de la importancia (tanto positiva como negativa) que la inducci�n iba a adquirir en la evoluci�n hist�rica del concepto del m�todo cient�fico, Arist�teles s�lo la menciona para resolver el problema planteado por su inter�s en la posesi�n de la esencia de las cosas: en realidad, la inducci�n es un producto colateral y no muy importante del esencialismo aristot�lico, y sirve para llegar a la posici�n en la que el cient�fico est� listo para generar nuevos conocimientos. En efecto, es cuando las generalizaciones alcanzadas por medio de la inducci�n se usan como premisas para la explicaci�n de las observaciones iniciales, cuando realmente avanza el conocimiento. El proceso l�gico responsable de este portento es la deducci�n, la operaci�n mental inversa de la inducci�n, o sea donde se va de lo general a lo particular. Arist�teles insisti� en que s�lo existe una forma general v�lida de deducci�n en la ciencia cuando la conclusi�n es que una clase de objetos o sucesos se incluye en otra, o se excluye de otra, ambas total o parcialmente. En forma semiesquem�tica, si A y B representan las dos clases mencionadas, las �nicas deducciones v�lidas entre ellas son las siguientes cuatro:

Deducción	Relación
Todos los A son B	A totalmente incluido en B
Ningún A es B	A totalmente excluido de B
Algunos A son B	A parcialmente incluido en B
Algunos A no son B	A parcialmente excluido de B

Sin embargo, la deducci�n m�s importante de estas cuatro es la primera, en vista de que la esencia de ciertas clases tiene relaciones especiales con la de otras clases, lo que se traduce en deducciones del tipo "Todos los A son B". Por esto mismo, el prototipo de la deducci�n cient�fica es el silogismo Barbara, que en forma esquem�tica corresponde a

Todos los A son B

Todos los C son A

Todos los C son B

Arist�teles se�al� cuatro requerimientos emp�ricos (o sea, no l�gicos) a las premisas de cualquiera deducci�n con pretensiones de calificar como explicaci�n cient�fica. Primero, que deber�an ser ciertas; segundo, que deber�an ser indemostrables; tercero, que deber�an ser mejor conocidas que la conclusi�n; y cuarto, que deber�an ser causas de los atributos mencionados en la conclusi�n. Lo que primero llama la atenci�n de estos requerimientos es que las premisas deban ser indemostrables, pues parece contradictorio con el papel previamente aceptado de la inducci�n como un mecanismo para alcanzar generalizaciones. Pero lo que preocupaba a Arist�teles (seg�n sus comentaristas) era que la �nica forma de evitar regresiones infinitas en las explicaciones cient�ficas era postular la existencia de algunos principios indemostrables en cada una de las ciencias; por lo tanto, no todo el conocimiento acumulado en cada ciencia es demostrable. Arist�teles especific� que esta propiedad la exhib�an las leyes cient�ficas m�s generales, as� como las definiciones de los significados de los atributos propios de cada ciencia. Pero este requerimiento de indemostrabilidad de las premisas de las deducciones cient�ficas no es el que llama m�s la atenci�n de los cuatro mencionados, sino el de su relaci�n causal con los atributos de la conclusi�n. Arist�teles reconoci� que entre las premisas y la conclusi�n se pod�an dar dos tipos de correlaciones, causales y accidentales; para distinguirlas, propuso que en las correlaciones causales el atributo ocurre en todos y cada uno de los miembros de la clase incluida en la conclusi�n, se trata de una propiedad espec�fica y no de un efecto colateral de otros atributos, y pertenece a la esencia del sujeto. �ste es uno de los varios talones de Aquiles del esquema cient�fico aristot�lico, especialmente porque no se especifican las caracter�sticas propias de la esencia. Arist�teles apunt� que "animal" es un predicado esencial de "hombre", pero desgraciadamente agreg� "musical" como ejemplo de un predicado no esencial; de mayor trascendencia, una cosa es dar ejemplos de predicados esenciales y accidentales (que fue lo que hizo) y otra es estipular los criterios generales y espec�ficos para hacer tales distinciones (que fue lo que no hizo).

4) Teor�a de la causalidad. Debido a la enorme influencia que tuvo (y todav�a tiene) en los diferentes conceptos del m�todo cient�fico a trav�s de la historia, conviene resumir muy brevemente las ideas aristot�licas sobre la causalidad. Lo primero que debe mencionarse es que Arist�teles ten�a una noci�n de causa m�s amplia y generosa que la contempor�nea; en nuestro tiempo, la causa es algo (cosa o proceso) que hace que otro algo (tambi�n cosa o proceso) ocurra, mientras que para Arist�teles �sta era solamente parte de una historia mucho m�s compleja y elaborada para explicar la existencia o la naturaleza de cualquier cosa, era indispensable especificar cuatro tipos diferentes de causas: materiales, eficientes, formales y finales. Las causas materiales y eficientes son obvias, sobre todo cuando se sigue el ejemplo aristot�lico de una estatua (material = m�rmol; eficiente = la idea de la estatua en la mente del artista), mientras que las causas formales y finales son menos aparentes y requieren cierta clarificaci�n. Las causas formales se refieren a la esencia de los objetos, a su forma (impuesta en la hyl� o sustrato esencial de las cosas), o a la uni�n misma entre la hyl� y su forma sobrepuesta, que no era necesariamente una morfolog�a espec�fica sino que pod�a ser tambi�n una temperatura, un color o una textura diferentes. Las causas finales son algo aparte, que todos nosotros conocemos muy bien pero que formalmente tratamos de evitar. Arist�teles las caracteriz� como la actualizaci�n de propiedades potenciales, lo que hoy nadie podr�a rechazar en principio, especialmente si aceptamos que todos los organismos biol�gicos contenemos un programa que define y delimita, en t�rminos gen�ricos y quiz� no importantes a nivel individual, pero definitivos entre poblaciones distintas, no s�lo lo que somos sino tambi�n todo lo que podemos llegar a ser. Arist�teles pensaba que las cosas ocurren en parte porque la causa final (el telos) as� lo proyecta y lo exige, o sea que el futuro (que de alguna manera ya existe, no s�lo hoy sino desde siempre) determina el pasado y el presente. �sta es la premisa fundamental de la teleolog�a, una forma de "explicaci�n" de la existencia y desarrollo de los fen�menos naturales que tuvo gran popularidad entre los comentaristas medievales de Arist�teles, entre los opositores de la "nueva ciencia" en el Renacimiento, entre los partidarios de la Natur-Philosophie, en el siglo XIX y que desde siempre ha sido una de las piedras de toque de los animistas o vitalistas, as� como uno de los enemigos que han tratado de derrotar los deterministas o mecanicistas. Con la primera menci�n de esta contienda, mucho m�s ideol�gica y emocional que objetiva y racional, y que volveremos a encontrar varias veces en estas p�ginas, conviene terminar nuestro examen de algunas de las ideas m�s relevantes al m�todo cient�fico de los sistemas filos�ficos de Plat�n y Arist�teles, tambi�n conocidos como antiguos. Espero que en el resto de este volumen quede claro que lo antiguo no es sin�nimo ni de primitivo ni de equivocado. Como veremos, Plat�n y Arist�teles se hicieron (en el lenguaje y con los intereses de su tiempo) muchas de las preguntas m�s importantes que todav�a hoy nos planteamos, basados en poqu�sima informaci�n objetiva sobre el mundo real, sus respuestas fueron magn�ficas en su generalidad y todav�a hoy, 25 siglos despu�s de haber sido propuestas, se siguen discutiendo y, como resultado natural de ese debate continuo, siguen siendo aceptadas por unos y discutidas por otros.