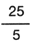8. Las representaciones de n�meros racionales

Corresponde a la sesi�n de GA 2.8 �POR F�N! �C�MO SE LLAMA?

Los n�meros racionales suelen ser representados en diferentes formas, la m�s usual es la de fracci�n com�n, de esta manera se realizan conversiones de un n�mero natural a fracci�n com�n y viceversa, adem�s de algunas otras.

Si se tiene la divisi�n de 25�5 y se representa esta operaci�n como 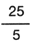, su resultado ser� un n�mero natural, el 5.

�Ser� posible representar este n�mero natural con una fracci�n com�n?

Desde luego que s�, ya que todo n�mero natural es un n�mero racional.

Si se tiene el caso de que el 5 o cualquier n�mero natural se quiere representar por medio de una fracci�n com�n, basta con agregarle como denominador el uno.

Ejemplos:

Cuando se desea representar a un n�mero natural en forma de fracci�n com�n, de tal manera que tenga un determinado denominador, se multiplica el n�mero natural por el denominador dado y el producto es el numero buscado.

Ejemplos:

Otra representaci�n es cuando se quiere llegar a una fracci�n decimal a partir de una fracci�n com�n; para realizar esta transformaci�n se divide el numerador entre el denominador.

Obs�rvese que 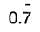es una fracci�n peri�dica, ya que el 7 se repite un n�mero de veces indeterminado; en tanto que 0.75 y 0.8 son fracciones finitas por tener n�mero limitado de cifras a la derecha del punto.

A continuaci�n se obtendr� la fracci�n com�n correspondiente a una fracci�n finita.

Para poder representar una fracci�n finita en fracci�n com�n, se conserva como numerador el n�mero decimal eliminando el punto, y como denominador la unidad seguida de tantos ceros como cifras tenga la parte decimal.

Obs�rvese que 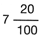es un n�mero racional al cual se le conoce como mixto en virtud de tener una parte entera y otra fraccionaria.

Por �ltimo se tratar� la conversi�n de un n�mero mixto a fracci�n com�n.

Cuando existen n�meros como 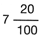, para obtener la fracci�n com�n se procede de la siguiente manera:

a) Obtener el numerador de la fracci�n impropia, multiplicando la parte entera por el denominador.

7 x 100

b) Posteriormente, al producto se le suma el numerador de la parte fraccionaria, quedando el mismo denominador.

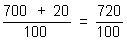
En muchas situaciones problem�ticas se utilizan los n�meros racionales y en algunas ocasiones se hace necesario representarlos en diferentes formas, con el objeto de. facilitar los c�lculos que se realicen con ellos.