Corresponde a la sesi�n de GA 2.13 FORMA Y FIGURA
La porci�n interior que determina un pol�gono se llama superficie y la medida de la misma se conoce como �rea. La medida del �rea de una figura se da en unidades cuadradas (m�, km�, pulgadas cuadradas, hect�reas, etc.).
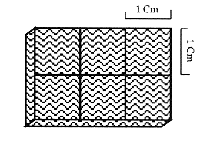
| En la figura mostrada (cuadril�tero), se han colocado peque�os trozos de madera de 1 cm de lado cada uno (1 cm�), cubriendo toda la superficie de la figura, obs�rvese que caben seis trozos exactamente, es decir, seis unidades cuadradas, lo que significa que el �rea de la figura es de 6 cm� | 
|
Las unidades del sistema m�trico decimal utilizadas para medir �reas son las siguientes:
Para obtener el �rea de figuras rectangulares (paralelogramos que tienen sus cuatro �ngulos rectos), es necesario considerar las medidas de su base y altura, en seguida se multiplican entre s�.
Hallar el �rea del siguiente rect�ngulo:
El �rea de este rect�ngulo es 12 cm�, esto se puede comprobar trazando en el interior de la figura unidades (cuadros) de un cent�metro de lado (1 cm�).
Si se establece que el �rea de cualquier rect�ngulo se representa con la letra "A", la base con la letra "b" y la altura con la letra "h" se tiene:
que es la f�rmula para hallar el �rea de cualquier rect�ngulo.
| El �rea del rect�ngulo es el producto de la medida de su base por la altura. |
En el caso del cuadrado, por ser �ste un cuadril�tero paralelogramo que tiene sus cuatro lados iguales y sus �ngulos rectos, su �rea se obtiene multiplicando la medida de uno de sus lados por s� mismo, esto es, elevando al cuadrado dicha medida.
Para hallar el �rea de un paralelogramo, �ste se puede transformar en un rect�ngulo si se trazan las alturas desde los v�rtices superiores.
Obs�rvese que se forman dos tri�ngulos AED y FBC los cuales son equivalentes, si se coloca el tri�ngulo AED sobre el tri�ngulo FBC se forma el rect�ngulo DEBC el cual tiene un �rea equivalente al paralelogramo original, por lo tanto, el �rea de �ste se halla con la misma f�rmula del rect�ngulo.
El �rea de un tri�ngulo se puede obtener de la siguiente manera: sea el tri�ngulo ABC, se traza una recta paralela a la base que pase por el v�rtice A, otra paralela al lado AB que se cruce con la primera en el punto C, obteni�ndose as� un paralelogramo.
Obs�rvese que se forman dos tri�ngulos congruentes (de igual medida), ABC y ACD; si el �rea de un paralelogramo se obtiene multiplicando la base por la altura, por lo tanto el �rea del tri�ngulo ABC ser� la mitad del �rea del paralelogramo, lo cual se representa con la siguiente f�rmula:
Hallar el �rea de un jard�n en forma triangular con las siguientes medidas.
Recu�rdese que el �rea de superficie de una figura geom�trica se mide en unidades cuadradas. Para hallar el �rea de cualquier paralelogramo se utiliza la f�rmula A = b.h, y la f�rmula correspondiente al �rea de un tri�ngulo es
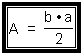
![[ Índice Conceptos Básicos ]](toc.gif)
![[ Previo ]](prevsec.gif)
![[ Nivel Superior ]](parntsec.gif)
![[ Siguiente ]](nextsec.gif)