14. Figuras geom�tricas

Corresponde a la sesi�n de GA 2.14 FIGURAS FAMOSAS

Existen dentro de los paralelogramos (figuras con sus lados opuestos paralelos) otras figuras, de las cuales es necesario saber determinar su �rea. Una de ellas se llama rombo (que tiene sus cuatro lados iguales y sus �ngulos iguales dos a dos).

Para determinar la f�rmula del �rea del rombo, es necesario hacer las siguientes consideraciones.

Sea el rombo LMNO

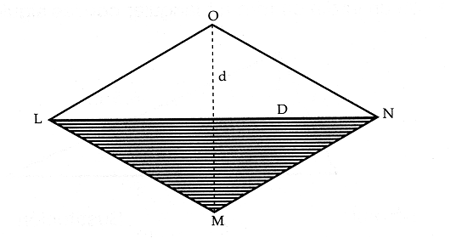
En donde D representa a la diagonal mayor y d la diagonal menor, las cuales dividen a la figura en cuatro tri�ngulos.

Si se trasladan los tri�ngulos inferiores (sombreados) coloc�ndolos arriba, se forma un rect�ngulo de �rea equivalente a la del rombo.

En la nueva figura, el largo es la diagonal mayor (D) del rombo y, la altura es la mitad de la diagonal menor (d) del rombo.

Si el �rea del rect�ngulo se obtiene con la f�rmula:

al simplificar los t�rminos queda de la siguiente manera:

en consecuencia:

El �rea de un rombo es igual al semiproducto de la diagonal mayor y la diagonal menor.

Hallar el �rea del siguiente rombo (la figura s�lo es una referencia).

La f�rmula que permite calcular el �rea del trapecio (cuadril�tero que solamente tiene dos lados opuestos paralelos) se obtiene haciendo las siguientes consideraciones:

Sea el trapecio LMNO

en donde:

pero como:

�rea del paralelogramo LMNO = �rea LMN + �rea LNO, entonces:

�rea del paralelogramo LMNO =

aplicando la propiedad distributiva y simplificando:

�rea del trapecio LMNO =

Por lo tanto:

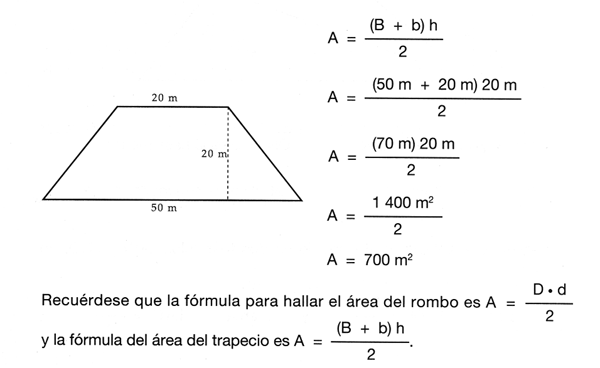
El �rea del trapecio es igual al producto de su altura por la semi suma de sus bases.

Ejemplo:

Hallar el �rea de un terreno que tiene la siguiente forma y cuyas medidas son las indicadas: (la figura es s�lo una referencia).