4. Las fuerzas

Corresponde a la sesi�n de GA 7.4 �FUERCITAS?

Las magnitudes se dividen en escalares y vectoriales.

Las magnitudes escalares son aquellas que para expresarlas s�lo necesitan la cantidad y la unidad, como la temperatura (20�C), la hora (6 p.m.), el �rea de un terreno (120 m�).

Para expresar las magnitudes vectoriales es necesario dar su magnitud,direcci�n y sentido y se representan por medio de vectores (flechas), como la velocidad y la fuerza.

Elementos de un vector

Los elementos caracter�sticas de un vector son:

Punto de aplicaci�n. Lugar donde se aplica una fuerza.

Direcci�n. L�nea sobre la cual act�a la fuerza: vertical, horizontal o inclinada.

Magnitud. Tama�o del vector de acuerdo con la escala que se est� utilizando.

Sentido. Indica hacia donde se aplica o dirige la fuerza.

La fuerza es una magnitud vectorial y se define como todo aquello capaz de producir: un movimiento, una deformaci�n o una presi�n.�sta puede cambiar de forma el cuerpo o cambiar la direcci�n o sentido del mismo.

La unidad de medida en el SI es el newton (N) y equivale a kgm/s�

Por lo tanto newton (N) = kgm/s�

La magnitud de la fuerza se mide con un dinam�metro, que consiste en un resorte que se deforma proporcionalmente a la carga que soporta por medio de una escala graduada en kilogramos fuerza o kilopondios, esta cantidad se multiplica 9.81 m/s� que es el valor de la fuerza de gravedad, obteni�ndose as� el resultado en newtons.

Sistema de ejes coordenados

La posici�n de un punto se representa en un Sistema de Ejes Coordenados.

Para esta representaci�n es necesario fijar una escala que es la relaci�n que existe entre la magnitud real y la dibujada.

Para representar una fuerza de 15 newtons en direcci�n norte, se utiliza una escala de 1 cm = 3 N.

Para saber cu�ntos cent�metros va a medir el vector se aplica una regla de tres.

Las fuerzas que se aplican sobre un cuerpo se pueden sumar o restar.

Los vectores o fuerzas se suman cuando tienen la misma direcci�n y sentido, y se restan cuando tienen la misma direcci�n y sentido contrario.

Sistemas de fuerzas

Generalmente, sobre un cuerpo act�an dos o m�s fuerzas, obteni�ndose as� un sistema de fuerzas, dichas fuerzas pueden ser sustituidas por una, llamada resultante. Las fuerzas que forman el sistema se conocen como componentes.

Los sistemas de fuerzas se clasifican en:

Colineales. Son las que act�an en una misma direcci�n.

Paralelas. Son aquellas cuyas direcciones son paralelas.

Concurrentes o angulares. Cuando las l�neas de acci�n convergen en un solo punto formando �ngulos.

Sistemas colineales

La resultante en estos sistemas se obtiene sumando algebr�icamente los componentes.

Ejemplo:

La resultante del siguiente sistema ser�

En forma gr�fica:

1. Se trazan los vectores tomando en cuenta la escala 1 cm = 1 N

2. Se colocan los vectores uno enseguida del otro y as� se obtiene la resultante.

Hay que tener presente que las fuerzas cuya direcci�n es hacia arriba o a la derecha se consideran positivas, y hacia abajo o a la izquierda, se consideran negativas.

Otro caso de fuerzas colineales se presenta cuando un componente es negativo.

Se suman algebr�icamente.

De forma gr�fica

1. Se trazan los vectores tomando en cuenta la escala que en este caso es de 1 cm = 1 N

2. Se traza la primera componente, donde termina se traza la segunda y as� sucesivamente, para terminar con los componentes, conservando sus caracter�sticas y obtener la resultante.

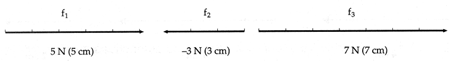
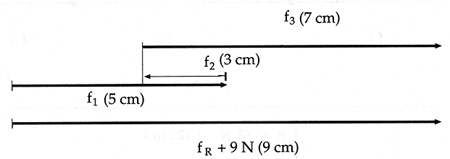
La forma de obtener la resultante en un sistema de fuerzas paralelas se explica a continuaci�n, siendo �sta tambi�n paralela.

Primer caso. Cuando tienen el mismo sentido.

Ejemplo: se tienen dos fuerzas paralelas que act�an sobre un cuerpo. Una es de 6 N y otra de2 N.

Forma gr�fica

1. Se trazan los vectores y se unen con una l�nea los puntos de aplicaci�n.

FUERZAS PARALELAS

2. La fuerza mayor se traza con sus mismas caracter�sticas en el punto de aplicaci�n de la menor.

3. La fuerza menor se traza en el punto de aplicaci�n de la fuerza mayor pero en sentido contrario.

4. Se unen los vectores trazados con una l�nea inclinada y donde se cruza �sta con la l�nea horizontal, se obtiene el punto de aplicaci�n del vector resultante cuyo valor ser� la suma de las fuerzas.

algebr�icamente

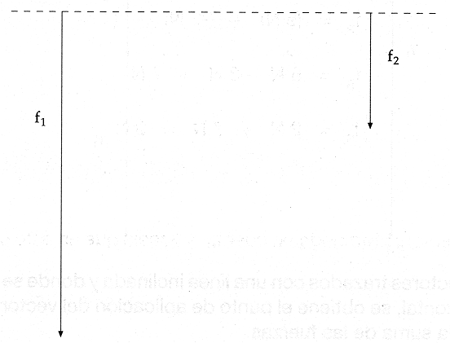
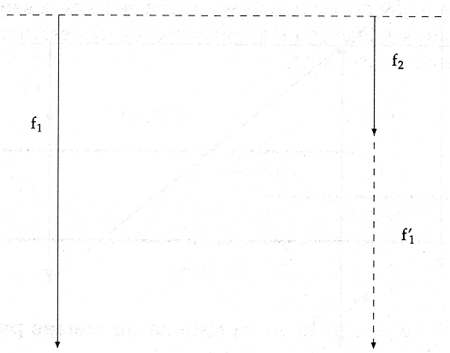
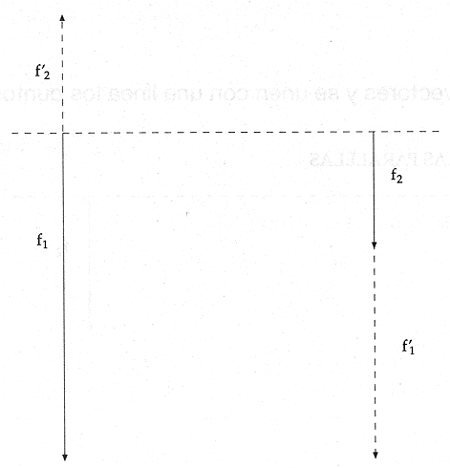
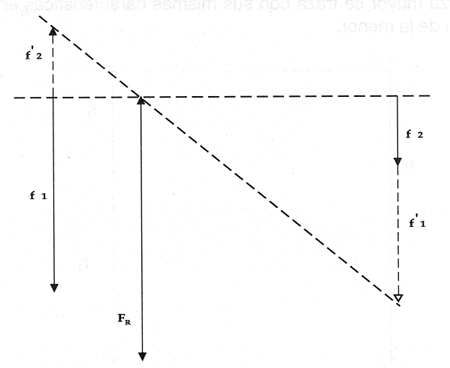
Segundo caso. Cuando las fuerzas paralelas son de sentido contrario y diferente magnitud.

Se suman algebr�icamente las fuerzas.

Ejemplo:

Para resolver este tipo de sistema de fuerzas, en forma gr�fica, se procede de igual forma que en el caso anterior para encontrar el punto de aplicaci�n de la fuerza resultante, la cual tendr� el sentido de la fuerza mayor.

Tercer caso. Cuando las fuerzas son paralelas, de igual magnitud y sentido contrario, este tipo de sistema es conocido como par de fuerzas, porque en �l no existe fuerza resultante, s�lo se produce giro, tal es el caso del volante de los autom�viles.

En un sistema de fuerzas angulares se utilizan m�todos gr�ficos para obtener la resultante, �stos son: el del paralelogramo y el del pol�gono.

El m�todo del paralelogramo se utiliza cuando s�lo act�an dos fuerzas, �ste consiste en:

1. Trazar los vectores partiendo de un mismo punto de aplicaci�n.

2. Trazar l�neas paralelas a las fuerzas, en forma punteada, obteniendo as� el paralelogramo.

3. Del punto de aplicaci�n de las tuerzas, al cruce de las l�neas auxiliares se traza una l�nea, obteniendo as� la resultante.

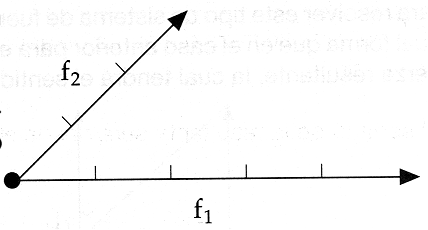
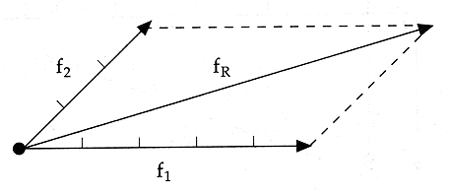
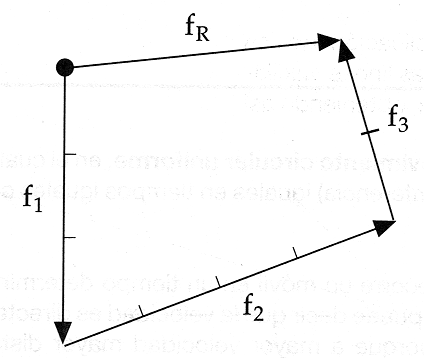
El m�todo del pol�gono es el que se utiliza para encontrar la resultante de m�s de dos fuerzas angulares.

Se coloca una fuerza a continuaci�n de otra, conservando sus caracter�sticas: magnitud, direcci�n y sentido.

La resultante se traza del punto de aplicaci�n de la primera fuerza al extremo de la �ltima.

El sentido de la resultante ser� desde el origen a la �ltima fuerza.