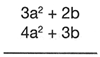
Corresponde a la sesi�n de GA 2.3 CHIQUITOS PERO IMPORTANTES
Las operaciones con polinomios presentan, para su resoluci�n, un algoritmo semejante a las aritm�ticas y la correcta aplicaci�n de las leyes de los exponentes ayuda a encontrar el resultado m�s f�cilmente.
Para encontrar el producto de dos polinomios deben obtenerse primero productos parciales, multiplicando cada uno de los t�rminos de un factor por cada uno de los t�rminos del otro factor.
1. Se colocan los factores en forma vertical:
2. Se multiplica uno de los t�rminos del segundo factor por cada uno de los t�rminos del primero.
3. Se multiplica el siguiente factor; los productos deben colocarse anotando en una columna los t�rminos semejantes:
4. Despu�s se suman estos t�rminos semejantes:
(3a� +2b) (4a� + 3b) = 12a4 + 17a�b +6b�
Real�cese ahora la multiplicaci�n:
Se alinean en forma vertical los factores:
Se obtienen los productos parciales de cada uno de los t�rminos del segundo factor por el primer polinomio.
Como en este ejemplo los productos parciales no tienen t�rminos semejantes, el resultado queda:
(4a + 2b) (3a - 6c) = 12a� + 6ab - 24ac - 12 bc
Divisi�n de un polinomio entre un monomio
Para dividir un polinomio entre un monomio basta con dividir cada uno de los t�rminos del dividendo entre el t�rmino del divisor.
aplicando la segunda ley de los exponentes se obtiene el resultado:
Divisi�n de un polinomio entre un polinomio
La divisi�n algebraica se realiza de manera semejante a la num�rica; y aplicando la ley de los exponentes y el algoritmo correspondiente es posible encontrar su cociente.
1. Se ordenan de manera decreciente los t�rminos de los polinomios, quedando la divisi�n:
2. Se obtiene el primer t�rmino del cociente dividiendo el primer t�rmino del dividendo entre el primer t�rmino del divisor:
3. Se anota como cociente y se multiplica por el divisor, se anotan los productos debajo del dividendo y se realiza la sustracci�n (sin olvidar el cambio de signo en el sustraendo).
4. Se baja el siguiente t�rmino y se siguen los pasos anteriores.
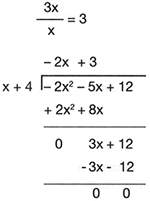
![[ Índice Conceptos Básicos ]](toc.gif)
![[ Previo ]](prevsec.gif)
![[ Nivel Superior ]](parntsec.gif)
![[ Siguiente ]](nextsec.gif)