4. Productos notables

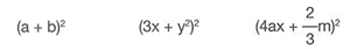
Corresponde a la sesi�n de GA 2.4 PROCESO ABREVIADO

Tanto en la multiplicaci�n algebraica como en la aritm�tica se sigue un algoritmo cuyos pasos conducen al resultado. Sin embargo, existen productos que responden a una regla cuya aplicaci�n lleva al resultado m�s f�cilmente; �stos reciben el nombre de productos notables. Algunos de ellos son los siguientes:

Cuadrado de un binomio

La expresi�n algebraica que consta de dos t�rminos se llama binomio y, al multiplicarse por s� misma, recibe el nombre de binomio al cuadrado.

Algunos ejemplos son los siguientes:

Si se obtiene la potencia (a + b)� con el algoritmo conocido, se tiene que:

De donde se puede establecer lo siguiente:

El cuadrado de un binomio es igual al cuadrado del primer t�rmino m�s (o menos) el doble producto del primero por el segundo t�rmino, m�s el cuadrado del segundo.

Ejemplo:

Obtener la potencia de: (3a - 2b)�

El cuadrado del primer t�rmino: (3a)� = 9a�,

menos el doble del primero por el segundo: -2(3a . 2b)= -12ab,

m�s el cuadrado del segundo: (2b)� = 4b�.

De donde se concluye que:

(3a - 2b)� = 9a� - l2ab + 4b�

Producto de dos binomios conjugados.

Se dice que dos binomios son conjugados cuando ambos tienen un t�rmino com�n y otro sim�trico.

Ejemplos:

En (a + b) (a - b), donde a es com�n, b y -b sim�tricos.

En (3x + y�) (3x - y�), 3x es com�n, y� y -y�, sim�tricos.

En (-2x + 5y) (2x + 5y), 5y es com�n, -2x y 2x, sim�tricos.

Obteniendo el producto de (a + b) (a- b) por el algoritmo conocido, se tiene que:

De donde se puede concluir que:

El producto de dos binomios conjugados es igual al cuadrado del t�rmino com�n menos al cuadrado del t�rmino sim�trico

Ejemplo:

Obteniendo el producto de (2a +5b) (-2a + 5b).

Se eleva al cuadrado el t�rmino com�n: (5b)� = 25b�,

menos el cuadrado del t�rmino sim�trico: -(2a)� = -4a�.

Por lo tanto:

(2a +5b) (-2a + 5b) = 25b� - 4a�

Producto de dos binomios con un t�rmino com�n

La expresi�n (a + b) (a + c) indica el producto de dos binomios, donde a es el t�rmino com�n y b y c son los t�rminos no comunes.

Algunos ejemplos de dos binomios con un t�rmino com�n son:

(4x + 8) (4x - 6), donde 4x es el t�rmino com�n.

(3a + 2b) (4c + 3a), donde 3a es el t�rmino com�n.

(x + 3y) (-2b + 3y), donde 3y es el t�rmino com�n.

Obteniendo el producto de (a + b) (a + c) por medio del algoritmo tradicional, se tiene que:

Con lo cual se llega a la regla siguiente:

El producto de dos binomios con un t�rmino com�n es igual al cuadrado del t�rmino com�n, m�s (o menos) el producto de la suma de los t�rminos no comunes por el t�rmino com�n, m�s (o menos) el producto de los t�rminos no comunes.

Ejemplo:

Obteniendo el producto de (5x + 5) (5x - 8).

Se eleva al cuadrado el t�rmino com�n: (5x)� = 25x�.

M�s (o menos) el producto de la suma de los t�rminos no comunes por el t�rmino com�n: (5 - 8) 5x = 25x - 40x = -15x.

M�s (o menos) el producto de los t�rminos no comunes: (5) (-8) = -40.

De donde se concluye que:

(5x + 5) (5x - 8) = 25x� - 15x - 40

La aplicaci�n de las reglas para obtener los productos notables facilita el proceso de resoluci�n y permite obtener el resultado m�s r�pidamente.