5. Factorizaci�n I

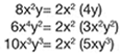
Corresponde a la sesi�n de GA 2.5 �SER� PERFECTO?

Factorizaci�n por factor com�n

La factorizaci�n es un proceso que permite descomponer en factores una expresi�n num�rica.

Por ejemplo:

6 = 3 x 2

Producto,6; Factor,3; Factor, 2

Recu�rdese que se llama factor a cada una de los n�meros que se multiplican para formar un producto.

Ahora bien, obs�rvense los siguientes ejemplos:

9 = 3 X 3

12 = 3 X 4

15 = 3 X 5

El n�mero 3 aparece como factor com�n de 9, 12 y 15 porque cada uno de estos n�meros se divide exactamente entre dicho factor com�n.

An�logamente, cuando una expresi�n algebraica est� contenida exactamente en todas y cada una de las expresiones de un polinomio, se dice que es factor com�n de ellas. As�, 2x� es factor com�n de 8x�y, 6x4y� y 1 0x�y� porque cada monomio puede dividirse exactamente entre 2x�, es decir:

El factor com�n de los t�rminos de un polinomio puede encontrarse en la forma siguiente:

Se busca el m�ximo com�n divisor (MCD) de los coeficientes de todos los t�rminos; y, de la literal o literales que aparezcan en todos los t�rminos, se escoge la que tenga menor exponente.

De esta forma, para factorizar un polinomio cualquiera que tenga un factor com�n se debe proceder como se muestra en seguida:

Factorizar el polinomio

Para factorizar el polinomio, se busca el MCD de los coeficientes. De esta manera se tiene:

Entonces el MCD de 9, 6,12, 3 = 3

Para encontrar la literal com�n, hay que observar cu�l es com�n a cada uno de los t�rminos y escoger la que tenga el menor exponente con el que aparece en el polinomio; en este caso, como hay dos literales que aparecen en todos los t�rminos, se deben escoger las de menor exponente. De esta manera, x� y y son las literales con menor exponente; por lo tanto, el factor com�n del polinomio es 3x� y.

Dividiendo el polinomio entre el factor com�n, se tiene:

Ahora bien, multiplicando el factor com�n por el cociente que resulta de dividir el polinomio dado entre dicho factor, resulta:

Ejemplo:

Factorizar el polinomio.

El MCD de los coeficientes es 2 y las literales comunes con menores exponentes son. a�b. Por lo tanto, el factor com�n es 2a�b.

Dividiendo el polinomio entre el factor com�n, se tiene:

Multiplicando el cociente por el factor com�n, resulta:

Obs�rvese otro ejemplo:

Factorizar el polinomio .

En este caso, el MCD es 1 y la literal com�n con menor exponente es Z�; por lo tanto, el factor com�n es Z�.

Dividiendo el polinomio entre el factor com�n, se tiene:

Multiplicando el cociente por el factor com�n, resulta:

Factorizaci�n de un trinomio cuadrado perfecto

Un trinomio cuadrado perfecto (T.C.P.) es el que resulta de elevar al cuadrado un binomio cualquiera.

Para identificar si un trinomio es cuadrado perfecto, v�ase si dos de sus t�rminos son cuadrados perfectos, y si el otro t�rmino corresponde al doble producto de las ra�ces cuadradas de los t�rminos cuadrados.

Ejemplo:

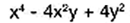es un trinomio cuadrado perfecto (T.C.P.), porque el primer y tercer t�rminos son cuadrados perfectos y, si se extraen sus ra�ces cuadradas, entonces se tiene que:

El doble producto de estas dos ra�ces es igual al segundo t�rmino del trinomio, es decir:

De esta manera, una vez que se ha identificado que un trinomio es cuadrado perfecto, se procede a factorizarlo estableciendo la relaci�n que hay entre �l y el binomio que lo origina, como se muestra en seguida:

Como se puede observar, el signo que separa el binomio es el signo del t�rmino no cuadr�tico del trinomio cuadrado perfecto.

V�ase c�mo se factoriza la siguiente expresi�n:

4a� + 12ab + 9b�

N�tese que es un T.C.P., porque el primer y tercer t�rminos son cuadr�ticos y el segundo t�rmino (l2ab) es el doble producto de las ra�ces del primer y tercer t�rminos correspondientes. Entonces, para factorizarlo, se obtienen las ra�ces de los t�rminos cuadr�ticos y se separan con el signo que tiene 12ab (en este caso es +); por lo tanto, resulta:

4a� + 12ab + 9b� = (2a + 3b)�

De esta forma, para factorizar un T.C.P., se extrae la ra�z cuadrada de cada uno de los t�rminos cuadr�ticos, los cuales se relacionan con el signo del segundo t�rmino del trinomio para formar el binomio y �ste se eleva al cuadrado.