6. Factorizaci�n II

Corresponde a la sesi�n de GA 2.6 DE DOS EN DOS O SEPARA... DOS

Factorizaci�n de una diferencia de cuadrados

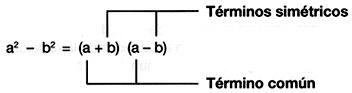
Una diferencia de cuadrados es el resultado del producto de dos binomios conjugados, es decir:

Entonces, para factorizar una diferencia de cuadrados, se buscan dos binomios conjugados cuyo producto sea igual que la diferencia de cuadrados propuesta.

Ejemplo 1:

Para factorizar la expresi�n 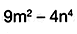, se debe proceder como se muestra en seguida.

El t�rmino 9m� es el cuadrado de 3m, que es el t�rmino com�n de los binomios que se buscan. El segundo t�rmino, 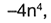es el producto de 2n� por -2n�, t�rminos sim�tricos de los binomios conjugados que se buscan.

Entonces,

De esta forma, para factorizar una diferencia de cuadrados, se buscan dos binomios conjugados cuyo t�rmino com�n se encuentra extrayendo la ra�z cuadrada del minuendo; y los t�rminos sim�tricos se obtienen anteponiendo signo positivo y negativo a la ra�z cuadrada del sustraendo

Ejemplo 2:

4x� -81y� = (2x + 9y) (2x - 9y),porque:

Factorizaci�n de un trinomio de segundo grado

Para factorizar un trinomio de la forma x� + b x + c, cuando resulta de multiplicar dos binomios con un t�rmino com�n, se debe proceder de la siguiente manera:

Ejemplo 1:

Factorizar el trinomio x� + 9x + 14

Paso 1. Extraer ra�z cuadrada a 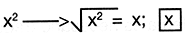es el t�rmino com�n

Paso 2. Buscar dos n�meros tales que sumados den 9 y multiplicados den 14.

Sumados 2 +7 = 9

Multiplicados 2(7) = 14

T�rminos no comunes 2,7

Paso 3. Expresar el trinomio en funci�n del producto de dos binomios con un t�rmino com�n:

x� +9x+14=(x+2)(x+7)

Ejemplo 2:

Factorizar el trinomio m� - 4m - 5

Paso 1. Ra�z cuadrada de 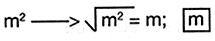es el t�rmino com�n

Paso 2. Los n�meros que sumados dan -4 y multiplicados dan -5 son:

Sumados + 1 - 5 = -4

Multiplicados (+1) (-5) = -5

Por lo tanto: m� -4m - 5 = (m + 1) (m - 5).

De esta forma, para factorizar un trinomio de la forma x� + bx + c se deben buscar dos binomios cuyo t�rmino com�n sea la ra�z cuadrada del t�rmino x�, es decir, x, y cuyos t�rminos no comunes cumplan la doble condici�n de que su suma sea igual al coeficiente del t�rmino en x; y su producto igual al t�rmino independiente.