7. Ecuaciones lineales

Corresponde a la sesi�n de GA 2.7 LOS DE ABAJO CAUSAN PROBLEMAS

Para resolver un problema es necesario traducirlo al lenguaje algebraico.

Por ejemplo:

Por cada libro que compr� Ana, pag� $ 1.50 de IVA, si por cuatro libros pag� $ 66.00, �cu�l fue el costo de cada libro?

precio de un libro: x

precio de un libro m�s IVA: x + 1.50

ecuaci�n: 4(x + 1.50) = 66

Obs�rvese que la ecuaci�n obtenida es lineal con par�ntesis. Para resolverla se deben tener en cuenta las leyes de los signos, as� como las propiedades de la igualdad.

En primer lugar se efect�a la operaci�n indicada (multiplicaci�n), para eliminar el par�ntesis:

4(x+ 1.50)=66

4x + 6 = 66

A continuaci�n se procede a resolver la ecuaci�n equivalente a la original, agrupando t�rminos semejantes:

4x + 6 = 66

4x = 66 - 6

4x = 60

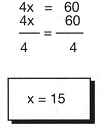
por �ltimo, se despeja la inc�gnita:

El resultado se comprueba si se le sustituye en la ecuaci�n original:

4(x + 1.50) = 66

4(15 + 1.50) = 66

4(16.50) = 66

66 = 66

Por lo tanto, el costo de cada libro fue de $ 15.00.

Otro ejemplo de resoluci�n de ecuaciones con par�ntesis es el siguiente:

- 5(y + 8 ) = 10(y + 2)

Se efect�a la multiplicaci�n en ambos miembros de la igualdad:

- 5(y + 8 = 10(y + 2)

- 5y - 40 = 10y + 20

se agrupan los t�rminos semejantes:

- 5y - 40 = 10y + 20

- 5y - 10y = 20 + 40

- 15y = 60

se despeja la inc�gnita:

el resultado se comprueba sustituy�ndolo en la ecuaci�n original:

- 5(y + 8) = 10(y + 2)

- 5(-4 + 8) = 10(-4 + 2)

20 - 40 = -40 + 20

-20 = -20

En algunos casos, las ecuaciones lineales presentan la caracter�stica de tener coeficientes fraccionarios. El siguiente ejemplo muestra el procedimiento para su resoluci�n:

Se convierte la ecuaci�n en otra equivalente con coeficientes enteros, esto se logra multiplicando ambos miembros de la ecuaci�n por el m�nimo com�n m�ltiplo de los denominadores:

el mcm de4 y 3 es 12

se agrupan los t�rminos semejantes:

18 + 8x = 120 + 6 + 4

26x = 130

se despeja la inc�gnita:

Se comprueba el resultado al sustituirlo en la ecuaci�n original:

Aprender a resolver ecuaciones con par�ntesis y coeficientes fraccionarios representa contar con una herramienta importante que permitir� resolver muchas situaciones expresadas en lenguaje com�n y que deben traducirse al lenguaje algebraico para obtener la soluci�n de la manera m�s pr�ctica posible.