8. Sistemas de ecuaciones 2 x 2

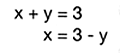
Corresponde a la sesi�n de CA 2.8 IGUALA SUS VALORES

Existen varios m�todos algebraicos para resolver un sistema de ecuaciones lineales con dos inc�gnitas; entre ellos se encuentra el m�todo de igualaci�n.

Obs�rvese c�mo se soluciona el siguiente problema, utilizando para ello el m�todo de igualaci�n.

Adriana compra en la papeler�a una pluma y un l�piz y paga $ 3.00. Ana Lilia compra dos plumas y tres l�pices del mismo precio y paga $ 7.00. �Cu�l ser� el costo de una pluma y cu�l el de un l�piz?

Si x representa el precio de una pluma y y el de un l�piz, entonces:

la compra de Adriana se representa con la ecuaci�n: x + y = 3

la compra de Ana Lilia se representa con la ecuaci�n: 2x + 3y = 7

y con ellas se forma un sistema de ecuaciones lineales con dos inc�gnitas:

x + y =3 ............................. ecuaci�n 1

x + 3y =7 ............................. ecuaci�n 2

para resolverlo por el m�todo de igualaci�n, se despeja la variable x en ambas ecuaciones:

Ecuaci�n 1

Ecuaci�n 2

se igualan los valores de la variable despejada:

Ecuaci�n 3

de este modo, se obtiene la ecuaci�n 3, que es una ecuaci�n lineal con una inc�gnita.

Se multiplica ambos miembros de la ecuaci�n por 2 para obtener una ecuaci�n equivalente con coeficientes enteros:

6 - 2y = 7 - 3y

se agrupan y reducen los t�rminos semejantes:

- 2y + 3y = 7 - 6

y = 1

al sustituir el valor de y en cualesquiera de las dos ecuaciones se obtiene el valor de la otra inc�gnita:

x = 3 - y

x = 3 - 1

x = 2

para comprobar los valores de las inc�gnitas, se sustituyen en las dos ecuaciones originales:

Por lo tanto, el precio de una pluma es de $ 2.00 y el de un l�piz, $ 1.00.

Los pasos necesarios para resolver, por el m�todo de igualaci�n, un sistema de ecuaciones con dos inc�gnitas son los siguientes:

1. Despejar en ambas ecuaciones la misma inc�gnita.

2. Igualar los valores de la inc�gnita despejada.

3. Resolver la ecuaci�n con una inc�gnita y encontrar su valor.

4. Sustituir este valor en cualesquiera de las ecuaciones originales para hallar el valor de la otra inc�gnita.

5. Comprobar los valores encontrados sustituy�ndolos en las dos ecuaciones originales.