Corresponde a la sesi�n de GA 2.9 PURAS Y MIXTAS
En diversas ocasiones, al traducir el enunciado de un problema al lenguaje algebraico, se obtiene una ecuaci�n. Esa ecuaci�n puede tener m�s de una inc�gnita o puede suceder que su �nica inc�gnita est� elevada a alguna potencia. Como ejemplo, consid�rese la siguiente situaci�n.
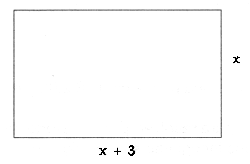
El grupo de danza folkl�rica de cierta localidad va a participar en un concurso regional. Para preparar adecuadamente su coreograf�a se requiere conocer las dimensiones del sal�n en el que se llevar� a cabo la competencia. La �nica persona del grupo que conoce el sal�n les informa que el piso en el que van a bailar tiene un �rea de 70 m� y que mide 3 m m�s de largo que de ancho. Entonces �cu�les son sus dimensiones?
Para buscar la soluci�n del problema se debe proceder as�:
a) Si el ancho de la pista de baile se representa con x, el largo es x + 3 y, si se dibuja la figura representativa, se tiene que:
b) Como la figura es un rect�ngulo, su �rea se obtiene multiplicando largo por ancho, o sea:
Al efectuar la multiplicaci�n indicada por medio del par�ntesis, se tiene:
En esta ecuaci�n, el mayor exponente de la inc�gnita es dos, por lo cual se le llama ecuaci�n de segundo grado o cuadr�tica. Si se elimina el t�rmino independiente (70) del segundo miembro, se tiene que:
Esta es la forma cl�sica de una ecuaci�n cuadr�tica completa, cuya forma general es:
Al comparar la ecuaci�n que se obtuvo del problema con la forma general de la cuadr�tica completa, se observa que:
donde a es el coeficiente de x� (que en este caso no se escribe porque es uno), en el ejemplo a = 1, b es el coeficiente de x, o sea, x = 3 y c es el t�rmino independiente. Entonces c = - 70.
Es necesario considerar que en una ecuaci�n de segundo grado o cuadr�tica puede faltar el t�rmino bx o el t�rmino independiente c, pero no el t�rmino ax� pues en ese caso la ecuaci�n ya no ser�a de segundo grado. A estas ecuaciones se les llama cuadr�ticas incompletas.
Si falta el t�rmino bx, la ecuaci�n es incompleta y tendr� la forma: ax� + c = 0 �sta recibe el nombre de cuadr�tica pura.
Si falta el t�rmino independiente c, la ecuaci�n es incompleta y tendr� la forma: ax� + bx = 0. Se le llama cuadr�tica mixta.
Naturalmente, el procedimiento para resolverlas tiene que ser diferente, dada la forma distinta de ellas: ax� + c = 0 y a� + bx = 0
As�, se tienen ecuaciones cuadr�ticas de la forma ax� + c =0
Resu�lvase la siguiente ecuaci�n: 3x� - 48 = 0
Como su forma general es ax� + c = 0, conviene resolver simult�neamente tanto la ecuaci�n como su forma general para obtener, con ello, una f�rmula que se aplique a este tipo de ecuaciones.
T�mese en cuenta que es necesario emplear las propiedades de la igualdad y realizar las operaciones indicadas, dejando en el primer miembro al t�rmino que contiene a la inc�gnita (ax�) y en el segundo miembro al t�rmino independiente (c), como se ve a continuaci�n.
Las dos ra�ces cuadradas de 16 son :
Por otra parte, la expresi�n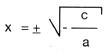 
puede utilizarse como f�rmula para resolver ecuaciones cuadr�ticas puras.
As�, hay ecuaciones cuadr�ticas de la forma ax� + bx = 0
Resu�lvase la siguiente ecuaci�n 3x� - 6x = 0.
Al observar que su forma general es ax� + bx =0, conviene resolver simult�neamente la ecuaci�n y su forma general para obtener una f�rmula que pueda ser aplicada al resolver ecuaciones de este tipo, empleando la factorizaci�n y una caracter�stica muy especial de la multiplicaci�n: Si uno de los factores es cero, el producto es cero.
Se toma en cuenta que x es factor com�n en el primer miembro y se factoriza:
Luego, se considera que el producto de cualquier n�mero por 0 es 0, lo que significa que uno de los factores (x o 3 x - 6) es 0, o los dos factores equivalen a 0, ya que 0 x 0 = 0. Si x= 0, entonces se expresa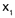 
=0.
Si 3x - 6 = 0 y ax + b = 0, se tiene :
Luego, en una cuadr�tica mixta la inc�gnita tiene 2 valores, siendo uno de ellos 0, o sea:
La expresi�n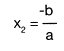 
se puede aplicar como f�rmula para obtener la soluci�n de las cuadr�ticas mixtas.
Cuando las ecuaciones cuadr�ticas incompletas se pueden resolver con seguridad y eficiencia, se tiene la posibilidad de dar soluci�n a una gran cantidad de problemas.
Ahora bien, el problema enunciado al inicio de este texto dio origen a la ecuaci�n x� + 3x - 70 = 0, que es una ecuaci�n cuadr�tica completa. El procedimiento para resolverla se ver� m�s adelante
![[ Índice Conceptos Básicos ]](toc.gif)
![[ Previo ]](prevsec.gif)
![[ Nivel Superior ]](parntsec.gif)
![[ Siguiente ]](nextsec.gif)
