15. Teorema de Pit�goras

Corresponde a la sesi�n de GA 2.15 DIMENSI�N DESCONOCIDA

El teorema de Pit�goras ha sido una herramienta muy importante en el conocimiento y c�lculo de grandes distancias.

Este teorema dice que en un tri�ngulo rect�ngulo la suma del �rea de los cuadrados construidos sobre los catetos es igual al cuadrado construido sobre la hipotenusa.

Una de esas demostraciones puede hacerse con base en el teorema de semejanza de tri�ngulos. V�ase:

Si el 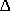ABC es rect�ngulo, entonces (AC)� + (CB)� = (AB)� es decir, b� + a� = c�

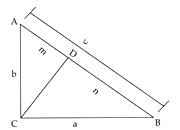
El 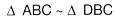por el teorema de tri�ngulos semejantes, que dice:

Si en un tri�ngulo rect�ngulo se traza la altura correspondiente a la hipotenusa, los dos tri�ngulos formados son semejantes entre s�, y semejantes al tri�ngulo dado.

Como: , entonces cn = a�

, entonces cm = b�

Al sumar las igualdades cn = a� y cm = b�, se tiene:

cn + cm = a� + b�

Si se factoriza el primer miembro de esta igualdad, se tiene:

c (n + m) = a� + b�

Pero, n + m = c, entonces (c) (c) = a� + b� , por lo tanto:

c� = a� + b�

Una aplicaci�n de dicho teorema puede observarse en el siguiente ejemplo:

Se quiere conocer el �rea de un terreno en forma de tri�ngulo is�sceles y se tiene que la medida de los dos lados iguales es 15 m y la del tercero es 24 m.

Como ya sabe, para calcular el �rea de un tri�ngulo es necesario saber cu�nto mide la base y cu�nto la altura. El siguiente dibujo representa el terreno del problema ya planteado.

La altura es un valor que se desconoce, pero se puede calcular por medio del teorema de Pit�goras, pues se sabe que la altura de un tri�ngulo es la perpendicular a la base. Esto es:

Una vez conocida la altura del tri�ngulo, se sustituyen valores en la f�rmula del �rea, es decir:

La utilidad de! teorema de Pit�goras es evidente en muchas actividades pr�cticas que realiza el hombre.