16. Segmentos notables en pir�mides y conos

Corresponde a la sesi�n de GA 2.16 L�NEAS DISTINGUIDAS

Como ya se sabe, la geometr�a es una rama muy importante de la matem�tica, y su estudio se considera fundamental no s�lo para quien se dedica al campo de esta disciplina, sino como una herramienta que sirve de apoyo en diversos campos de la ciencia y la tecnolog�a.

En estas p�ginas se ver�n los segmentos m�s importantes considerados para el cono y la pir�mide.

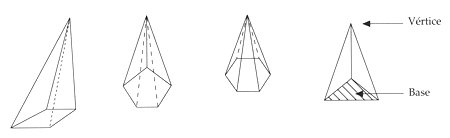
Las pir�mides son cuerpos formados por una base con forma de cualquier pol�gono y tantas caras triangulares como lados tenga la base.

Los segmentos m�s importantes en estos cuerpos son las aristas, que corresponden a la uni�n de todas las caras del cuerpo; la altura, que es la distancia que va del v�rtice hacia la base en forma perpendicular y el apotema, que es la altura de cualesquiera de los tri�ngulos laterales.

Ahora imag�nese un tri�ngulo rect�ngulo girando sobre uno de sus catetos.

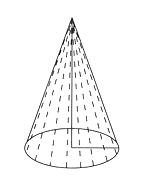Al hacer un giro completo y llegar al punto de inicio, el tri�ngulo rect�ngulo describe un cono.

Si se analiza bien el giro del tri�ngulo, la hipotenusa de �ste es la generatriz del cono, el cateto sobre el que gira representa el radio de la base y el otro cateto del tri�ngulo representa la altura del cono.

Con base en lo expuesto y para calcular la longitud de cualesquiera de esos segmentos se recurre al teorema de Pit�goras, como se muestra en los siguientes ejemplos:

1. Calcular la medida del apotema de una pir�mide cuadrangular, cuya base mide 16 m� y su arista mide 10 m.

Si como dato se tiene que la base mide 16 m�, para conocer la medida de uno de sus lado le extrae ra�z cuadrada.

La base mide 4 m por lado, pero el apotema de la pir�mide es igual que la altura de una de sus caras triangulares y, a su vez, ella siempre es la mediatriz, por lo que las medidas quedan de la siguiente forma:

Por lo tanto, la medida del apotema es de 9.8 m en n�meros redondos.

2 �Cu�nto medir� la altura de un cono, cuya generatriz mide 24 cm y el radio de la base mide 8 cm?

As� que la altura del cono mide 22.63 cm

Como puede verse, apoy�ndose en el teorema de Pit�goras es muy f�cil obtener la medida de los segmentos notables en pir�mides y conos.

* Cantidad redondeada