17. Razones trigonom�tricas

Corresponde a la sesi�n de GA 2.17 �TIENES RAZ�N?

La trigonometr�a, en sus inicios, se concret� al estudio de los tri�ngulos. Por varios siglos se emple� en topograf�a, navegaci�n y astronom�a.

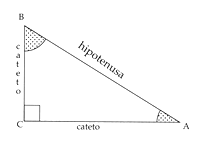
Para establecer las razones trigonom�tricas, en cualquier tri�ngulo rect�ngulo, es necesario conocer sus elementos. Por ejemplo:

Los �ngulos de A y B son agudos

El �ngulo C es recto.

Puede notarse que los lados de los �ngulos agudos son la hipotenusa y un cateto y los del �ngulo recto son catetos.

Considerado uno de los �ngulos agudos del tri�ngulo rect�ngulo e identificada previamente la hipotenusa, es necesario diferenciar los catetos.

Cateto adyacente es aquel que forma parte del �ngulo al cual se hace referencia.

Cateto opuesto es el lado que no forma parte del �ngulo que se toma como referencia y se encuentra enfrente de �ste.

Obs�rvense los siguientes tri�ngulos:

N�tese que los lados del tri�ngulo se representan con las dos letras may�sculas que corresponden a sus puntos extremos, colocando sobre ellas una l�nea horizontal, o bien, con una sola letra min�scula.

Las razones trigonom�tricas se establecen entre dos lados de un tri�ngulo rect�ngulo en relaci�n con uno de sus �ngulos agudos.

En el siguiente cuadro se observan las seis razones trigonom�tricas que se pueden establecer, para cualesquiera de los �ngulos agudos, en un tri�ngulo rect�ngulo.

Seno y cosecante

En un tri�ngulo rect�ngulo, el seno y la cosecante de cualesquiera de sus �ngulos agudos (x), se expresan con las razones siguientes:

Coseno y secante

En un tri�ngulo rect�ngulo, las razones del coseno y la secante de cualesquiera de sus �ngulos agudos (x) son:

Tangente y cotangente

La tangente y cotangente de cualesquiera de los �ngulos agudos (x) de un tri�ngulo se establece con las siguientes razones:

En el cuadro se resumen las seis funciones trigonom�tricas para cualquiera de los �ngulos agudos de un tri�ngulo rect�ngulo

Puede notarse que las funciones trigonom�tricas fundamentales y sus rec�procas tienen invertidos sus t�rminos.