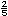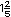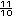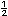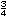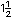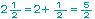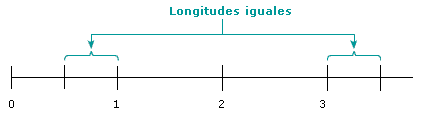Fracciones y decimales en la
recta num�rica
|
| En esta secuencia trabajar�s
en la representaci�n de n�meros fraccionarios y decimales en la recta num�rica
a partir de distintas informaciones, analizando las convenciones de esta
representaci�n. |
Sesi�n 1
EL SALTO DE ALTURA
>>>Para empezar
 |
El salto de altura |
El salto de altura es una de las competencias atl�ticas m�s
atractivas. Se trata de saltar sobre una barra horizontal que est� colocada a
varios metros sobre el nivel del piso. �Los mejores atletas saltan m�s de 2
metros de altura!
Para decidir cu�ndo un competidor gana o pierde una
competencia es muy importante medir de modo muy preciso la altura de sus
saltos. Las mediciones de los saltos se pueden realizar usando fracciones y
n�meros decimales.
La tabla muestra tres marcas conseguidas en el salto de altura
por distintos atletas.
| A�o |
Competencia |
Atleta |
Longitud aproximada del
salto (metros) |
| 1993 |
Campeonato Mundial de Atletismo |
Javier Sotomayor |
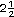 |
| 1996 |
Juegos Ol�mpicos de Estados Unidos |
Charles Austin |
|
| 2004 |
Juegos Ol�mpicos de Atenas |
Stefen H�lm |
|
>>>Consideremos lo siguiente
 |
En la siguiente recta se ha representado el
salto de Sotomayor. Anota en el lugar correspondiente la representaci�n de la
distancia que saltaron Austin y H�lm. |
Recuerda que: Un n�mero mixto se puede expresar como una
fracci�n impropia. Por ejemplo,
|
-
| a) |
�Qui�n hizo el salto de mayor altura?
___________________________ |
-
| b) |
�Qui�n hizo el salto de menor altura?
___________________________ |
 |
Comparen sus respuestas y comenten c�mo las
obtuvieron. |
>>>Manos a la obra
-
 |
| I. |
Ubica en la siguiente recta los
n�meros 1,
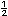 y 1 y 1
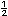 . . |
|
|
|
-
| a) |
En la misma recta ubica al 3. |
-
| b) |
�C�mo supiste d�nde va el 3? _____________________________ |
-
| c) |
Con tu regla mide la distancia del 0 al 1.
�Cu�nto es? ____________ |
�y la distancia de 1 a 2? ____________, �y la de 2 a 3? ____________
Verifica que estas tres distancias sean iguales, si no es as� revisa
en d�nde est� el error.
-
| II. |
Considera ahora s�lo la distancia de 2 a
3. |
|
|
-
| a) |
Ubica el punto
 (altura que salt� H�lm) (altura que salt� H�lm) |
-
| b) |
�Qu� hiciste para localizar el punto
 ?_______________________________________________ ?_______________________________________________ |
-
| c) |
Hay muchas maneras de dividir un segmento en tres
partes iguales, a continuaci�n se presenta una. |
-
| 1. |
Necesitas una hoja rayada. |
|
-
| 2. |
Tomas la hoja de papel y colocas una de las
rayas al inicio del segmento que quieres dividir. |
|
|
|
|
-
| 3. |
Giras la hoja hasta que tres renglones corten
al segmento que quieres dividir. |
|
-
| 4. |
Pones una marca en cada corte �y listo! el
segmento queda dividido en tres partes. |
|
|
|
|
-
| d) |
Utiliza el procedimiento anterior para dividir
segmentos en tres partes iguales y ubica en la recta
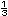 , ,
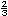 , ,
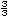 , ,
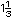 , ,
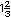 , ,
 . . |
-
| e) |
Verifica que el segmento que va de 0 a 1 haya
quedado dividido en tres partes iguales. Puedes usar tu regla para medir la
longitud de las partes. |
El n�mero de renglones que debes considerar es igual al n�mero
de partes en que quieres dividir el segmento; por ejemplo, si quieres dividirlo
en cinco partes, giras la hoja hasta que cinco renglones corten al
segmento.
-
| III. |
Considera la recta y ubica los puntos que
corresponden a
 , ,
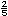 , ,
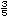 , ,
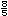 , ,
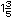 , ,
 , ,
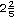 . . |
|
|
Utiliza tu regla para verificar que el segmento que va de 1 a
2 haya quedado dividido en cinco partes iguales.
 |
Regresen al problema inicial y verifiquen,
apoy�ndose en el procedimiento de la hoja rayada, si localizaron bien los
saltos de Austin y H�lm. Despu�s, con ayuda de su maestro, lean la siguiente
informaci�n. |
>>>A lo que llegamos
En la recta num�rica
pueden ubicarse fracciones.
Si se desea ubicar novenos en la recta, la
unidad en la que se va a ubicar debe quedar dividida en nueve partes iguales.
|
| Para ubicar n�meros en la
recta num�rica es importante que consideres que a diferencias iguales entre
n�meros deben corresponder distancias iguales. |
Por ejemplo,
a) la
distancia de 3 a 4 debe ser la misma que la de 4 a 5.
b) la distancia de
 a 1 debe ser la misma que la de 3 a a 1 debe ser la misma que la de 3 a
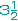 . . |
|
|
-
 |
| IV. |
Cada uno de los miembros de la
pareja localice la fracci�n
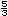 en la siguiente recta num�rica considerando los
puntos dados. H�ganlo por separado. en la siguiente recta num�rica considerando los
puntos dados. H�ganlo por separado. |
|
|
|
-
| a) |
Comparen sus rectas. En sus cuadernos dibujen
otra recta y encuentren otra manera correcta de localizar
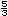 . . |
-
| b) |
En la recta B localicen
1 y 2. H�ganlo por separado y no se olviden de considerar los puntos
dados. |
-
| c) |
�En cu�ntas partes dividieron el segmento que va
de 0 a
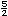 ? _______ ? _______ |
-
| d) |
Localicen otra vez la fracci�n
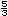 , pero ahora h�ganlo en la recta B. , pero ahora h�ganlo en la recta B. |
-
| e) |
�Llegaron los dos al mismo resultado? Comenten
c�mo lo obtuvieron. |
 |
Comparen sus respuestas y comenten: |
-
| a) |
�Cu�ntas maneras distintas encontraron para
localizar
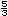 en la recta A? en la recta A? |
-
| b) |
�Cu�ntas maneras distintas hay para localizar
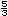 en la recta B? en la recta B? |
>>>A lo que llegamos
En una recta num�rica que
s�lo tiene localizado un n�mero, hay muchas maneras correctas de localizar
otro. Por ejemplo, en la recta A de la actividad anterior hay muchas maneras
distintas de localizar
 . . |
Si en la recta num�rica
est�n ya localizados dos puntos, entonces hay una sola manera de localizar
cualquier otro. Por ejemplo, en la recta B de la actividad anterior hay una
sola manera de localizar
 . . |
>>>Lo que aprendimos
 |
-
| 1. |
Usa una hoja rayada para
dividir segmentos en el n�mero de partes que se requiere y ubica las fracciones
que se indican. |
|
-
| 2. |
Anota el n�mero que corresponde a cada
punto. |
-
| 3. |
Ubica en la recta num�rica los n�meros
indicados. |
 |
Comenten sus respuestas con otros compa�eros.
Mencionen la manera en que hallaron los n�meros de la actividad 2. Con respecto
a la actividad 3, comenten acerca de cu�les incisos ten�an varias respuestas y
cu�les s�lo una y justifiquen por qu� ten�an una o varias respuestas. |




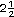




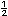 y 1
y 1
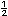 .
.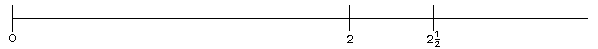

 (altura que salt� H�lm)
(altura que salt� H�lm) ?_______________________________________________
?_______________________________________________ 
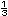 ,
,
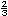 ,
,
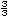 ,
,
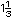 ,
,
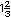 ,
,
 .
.
 ,
,
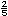 ,
,
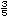 ,
,
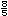 ,
,
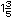 ,
,
 ,
,
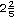 .
.

 a 1 debe ser la misma que la de 3 a
a 1 debe ser la misma que la de 3 a
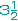 .
.
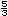 en la siguiente recta num�rica considerando los
puntos dados. H�ganlo por separado.
en la siguiente recta num�rica considerando los
puntos dados. H�ganlo por separado.
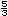 .
.
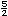 ? _______
? _______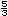 , pero ahora h�ganlo en la recta B.
, pero ahora h�ganlo en la recta B.
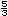 en la recta A?
en la recta A?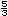 en la recta B?
en la recta B? .
.  .
.