Sesi�n 2
DENSIDAD Y FRACCIONES
>>>Para empezar
Entre dos fracciones siempre hay otra fracci�n. A esta
propiedad se le conoce como densidad de las fracciones. En esta sesi�n
estudiar�n esta propiedad.
>>>Consideremos lo siguiente
 |
Encuentren un n�mero que est� entre
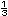 y y
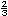 . Local�cenlo en la siguiente recta num�rica. . Local�cenlo en la siguiente recta num�rica. |
 |
Comparen sus respuestas y comenten c�mo las
obtuvieron. |
>>>Manos a la obra
-
 |
| I. |
Los alumnos de otra telesecundaria
dijeron que no hay ning�n n�mero entre
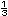 y y
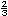 porque entre 1 y 2 no hay ning�n n�mero. porque entre 1 y 2 no hay ning�n n�mero.
Comenten: �Est�n de acuerdo con ellos?, �por
qu�? |
|
|
|
-
 |
| II. |
En la recta num�rica localicen los
n�meros 0 y 1.
El segmento que va de 0 a 1 queda dividido en tercios.
Verif�quenlo. |
|
|
|
-
| a) |
Dividan los tercios en sextos, �en cu�ntas partes
tienen que dividir cada tercio? _______________________________________________ |
-
| b) |
Entre
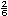 y y
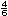 hay otra fracci�n con denominador 6, �cu�l es?
________ hay otra fracci�n con denominador 6, �cu�l es?
________
Local�cenla en la recta. |
-
| c) |
Dividan en novenos el segmento de 0 a 1, �en
cu�ntas partes tienen que dividir cada tercio? _____________________________________ |
-
| d) |
Encuentren y localicen en la recta tres n�meros
que est�n entre
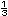 y y
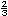 . �Cu�les son? . �Cu�les son? |
| __________________ |
� |
__________________ |
� |
__________________ |
 |
Comparen sus respuestas. |
>>>A lo que llegamos
| Entre cualquier par de
n�meros fraccionarios siempre hay otros n�meros fraccionarios. Esta es una
propiedad que se conoce como propiedad de densidad de
las fracciones. |
-
 |
| III. |
En las rondas eliminatorias para
el Campeonato Mundial de 2005, un competidor tuvo mejores marcas que H�lm, pero
no super� la marca de Austin. En la recta num�rica est�n representadas las
alturas que saltaron H�lm y Austin. |
|
|
|
Contesten:
�Cu�nto pudo haber saltado el nuevo competidor?
___________________
Representen esta altura en la recta num�rica.
-
 |
| IV. |
Los alumnos de otra telesecundaria
dijeron que no se puede resolver el problema anterior. Convirtieron los
resultados de Austin y de H�lm a quinceavos: |
|
|
|
Recuerden que:
Cuando en una fracci�n se multiplica
por el mismo n�mero al numerador y al denominador, se obtiene una fracci�n
equivalente. Por ejemplo:
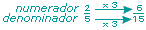
Entonces
 y y
 son equivalentes. son equivalentes. |
Charles Austin:
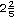 metros =
metros =
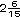 metros
metros
Stefen H�lm:
 metros =
metros =
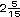 metros
metros
Y dijeron que entre
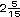 y
y
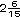 no hay ning�n n�mero.
no hay ning�n n�mero.
�Est�n de acuerdo con lo que dicen en esa
escuela? �Por qu�?
|
|
-
| V. |
En la recta num�rica localicen
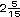 y y
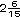 . Dividan en treintavos y encuentren: . Dividan en treintavos y encuentren: |
|
|
|
-
| a) |
�En cu�ntas partes hay que dividir cada quinceavo
para obtener treintavos?_______________________________________ |
-
| b) |
Exactamente a la mitad entre
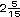 y y
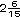 hay otro n�mero, �cu�l es? hay otro n�mero, �cu�l es?
_________________________________________________ |
-
| c) |
Sin dividir en la recta, encuentren las
siguientes equivalencias: |
-
| d) |
Entre
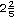 y y
 hay dos fracciones con denominador 45, �cu�les
son? hay dos fracciones con denominador 45, �cu�les
son? |
| ________________________ |
________________________ |
 |
Encuentren tres posibles saltos m�s altos que
 metros (Stefen H�lm), pero m�s bajos que metros (Stefen H�lm), pero m�s bajos que
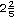 metros (Charles Austin): metros (Charles Austin): |
| _________________ |
_________________ |
_________________ |
>>>Lo que aprendimos
 |
-
| 1. |
En la siguiente recta num�rica ubica el
n�mero
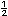 |
|
 |
Encuentra tres n�meros que est�n entre
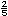 y
y
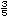 . Local�zalos en la recta.
. Local�zalos en la recta.
-
| 2. |
Encuentra tres n�meros que est�n entre
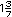 y y
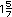 . Local�zalos en la siguiente recta
num�rica. . Local�zalos en la siguiente recta
num�rica. |




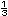 y
y
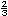 . Local�cenlo en la siguiente recta num�rica.
. Local�cenlo en la siguiente recta num�rica.


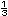 y
y
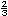 porque entre 1 y 2 no hay ning�n n�mero.
porque entre 1 y 2 no hay ning�n n�mero.

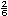 y
y
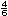 hay otra fracci�n con denominador 6, �cu�l es?
________
hay otra fracci�n con denominador 6, �cu�l es?
________
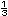 y
y
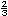 . �Cu�les son?
. �Cu�les son?

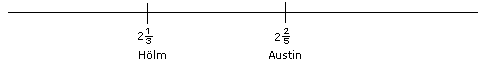

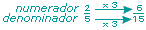
 y
y
 son equivalentes.
son equivalentes.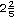 metros =
metros =
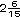 metros
metros metros =
metros =
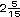 metros
metros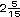 y
y
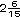 no hay ning�n n�mero.
no hay ning�n n�mero.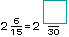
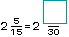
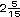 y
y
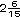 hay otro n�mero, �cu�l es?
hay otro n�mero, �cu�l es?

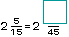
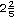 y
y
 hay dos fracciones con denominador 45, �cu�les
son?
hay dos fracciones con denominador 45, �cu�les
son?
 metros (Stefen H�lm), pero m�s bajos que
metros (Stefen H�lm), pero m�s bajos que
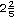 metros (Charles Austin):
metros (Charles Austin):
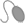

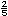 y
y
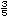 . Local�zalos en la recta.
. Local�zalos en la recta.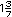 y
y
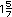 . Local�zalos en la siguiente recta
num�rica.
. Local�zalos en la siguiente recta
num�rica.