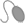Secuencia�5Matem�ticas I

Simetr�a

En esta secuencia tendr�s la oportunidad de construir figuras sim�tricas respecto a un eje, analizarlas y explicitar las propiedades que se conservan en figuras tales como: tri�ngulos is�sceles y equil�teros, rombos, cuadrados y rect�ngulos.

Sesi�n 1

COMO SI FUERA UN ESPEJO

>>>Para empezar

El Taj Mahal se encuentra en la India y por su dise�o y belleza es considerado una maravilla de la arquitectura. �Ya observaste c�mo se refleja en el agua?

Cuando el agua est� tranquila refleja las im�genes de los objetos y seres como si fuera un espejo.

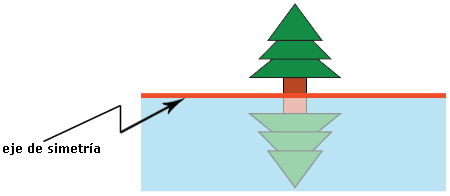
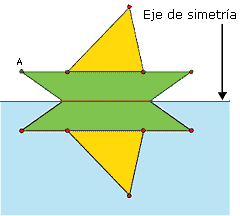
En la figura de la derecha el reflejo es sim�trico al �rbol con respecto a la l�nea roja.
Esa l�nea roja recibe el nombre de eje de simetr�a.

>>>Consideremos lo siguiente

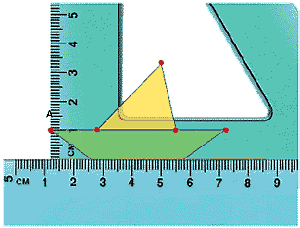
	�De qu� manera podr�a trazarse el sim�trico del barco con respecto a la l�nea roja? Planeen y lleven a cabo una manera para hacer el trazo con sus instrumentos geom�tricos.

Comenten con otros equipos el procedimiento que emplearon para trazar el sim�trico.

>>>Manos a la obra

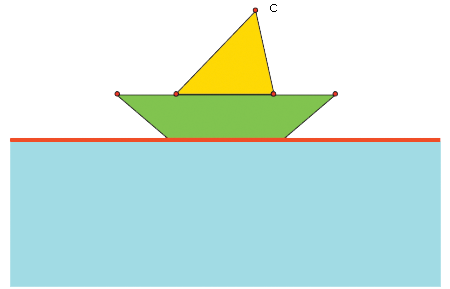
I.	En los siguientes dibujos el sim�trico no est� bien trazado. Corr�gelos.

II.	En el siguiente dibujo se ha trazado correctamente el sim�trico del barco.

Encuentra el punto que es el sim�trico de A, n�mbralo A’ (se lee A prima)

Se dice que A es el sim�trico de A’, o bien, que A es el correspondiente sim�trico de A'.

Recuerda que:
Las perpendiculares forman �ngulos de 90�. La distancia de un punto a una recta se mide por la perpendicular que va del punto a la recta.

Usa tu regla para unir A con A’, al hacerlo obtienes el segmento AA’.

a) �Cu�nto mide la distancia del punto A al eje de simetr�a?
__________________
b) �Cu�nto mide la distancia del punto A’ al eje de simetr�a?
__________________
c) �Cu�nto mide el �ngulo que forman el eje de simetr�a y el segmento AA’?
__________________

La distancia del punto A y de A’ al eje de simetr�a es la misma, es decir, el punto A y A’ equidistan del eje.
El eje de simetr�a y el segmento AA’ son perpendiculares.

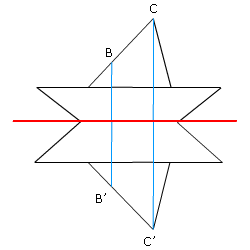
III.	Verifica que para los puntos B y C y sus sim�tricos se cumplen tambi�n las dos condiciones enunciadas en el recuadro anterior.

Anota en la figura las distancias de B, B’, C, C’ al eje y la medida de los �ngulos que forman el segmento BB’ y CC’ con el eje.

Elige otros dos puntos y sus sim�tricos y verifica que tambi�n se cumplen las condiciones mencionadas.

Esto que exploraste con algunas parejas de puntos sim�tricos pasa con cualquier pareja de puntos sim�tricos.

IV.	Verifica en el problema inicial que los puntos rojos y sus sim�tricos tambi�n cumplen esas dos condiciones.

>>>A lo que llegamos

Un punto es sim�trico a otro con respecto a una recta si y s�lo si se cumple que ambos puntos equidistan de la recta y el segmento que los une es perpendicular a la recta.

El sim�trico de un segmento con respecto a una recta es otro segmento.
Todos y cada uno de los puntos del segmento AB tienen su correspondiente sim�trico en el segmento A’B’.
El segmento A’B’ es el correpondiente sim�trico del segmento AB.