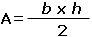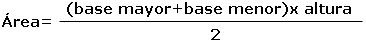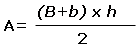Secuencia�14Matem�ticas I

Sesi�n 2

ROMPECABEZAS 2

>>>Para empezar

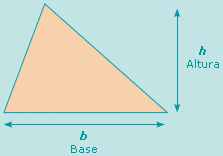
En la primaria aprendiste a calcular el �rea de los tri�ngulos. �C�mo se calcula el �rea de un tri�ngulo? __________________________________________

�Sabes por qu� se calcula as�? __________________________En esta lecci�n lo averiguar�s.

>>>Consideremos lo siguiente

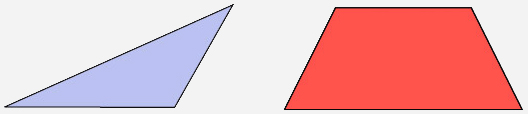
Calculen el �rea de las siguientes figuras.

Comenten los procedimientos y resultados a los que llegaron. En particular mencionen:

�Qu� medidas tomaron en cada figura?
�C�mo utilizaron estas medidas para calcular el �rea?
Si usaron alguna f�rmula, �saben c�mo se obtiene dicha f�rmula?

>>>Manos a la obra

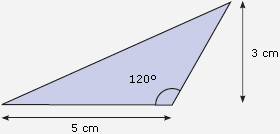
I.	Recorten dos tri�ngulos que midan lo que se indica.

a) Con los dos tri�ngulos cubran la superficie del siguiente romboide.

b) �Qu� parte del �rea del romboide es el �rea del tri�ngulo? _________
c) Completen la siguiente tabla:

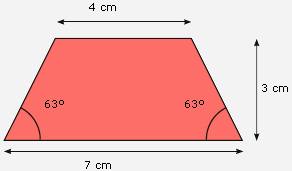
II.	Recorten dos trapecios que tengan las medidas que se indican en la figura.

a) Acomoden los dos trapecios de manera que cubran la superficie del siguiente romboide.

b)	Analicen las medidas de la base del romboide y las medidas de la base mayor y la base menor del trapecio y se�alen qu� relaci�n existe entre ellas. ___________________________________________________

c)	�Qu� parte del �rea del romboide es el �rea del trapecio? ___________________________________________________

d)	Escriban una regla o f�rmula para calcular el �rea de un trapecio cuando se conocen las medidas de sus bases y su altura ___________________________________________________

e) Completen las siguientes tablas:

Comenten ante su grupo los resultados que han obtenido hasta el momento. Escriban en el pizarr�n las f�rmulas que encontraron para calcular el �rea del tri�ngulo y del trapecio; si las f�rmulas son diferentes, comp�renlas e investiguen si son equivalentes.

>>>A lo que llegamos

El �rea de un tri�ngulo se calcula aplicando la siguiente f�rmula:

Si se denomina b a la base y
h a la altura, puede escribirse:

El �rea de un trapecio se calcula aplicando la siguiente f�rmula.

Si se denomina B a la base mayor, b a la base menor y h a la altura, puede escribirse: