Secuencia�16Matem�ticas I
|
|
Sesi�n 2
ESCALAS Y REDUCCIONES
>>>Para empezar
Imagina que fuera necesario hacer el dibujo en tama�o real de
una c�lula o de un edificio, �c�mo lo har�as? Con las escalas se pueden
representar objetos muy peque�os o muy grandes porque permiten reducir o
ampliar el tama�o real de los objetos de manera proporcional.
Una cancha reglamentaria de f�tbol debe ser un rect�ngulo con
las siguientes dimensiones: de largo debe medir entre 90 y 120 metros, y de
ancho entre 45 y 90 metros.
>>>Consideremos lo siguiente
 |
El siguiente es un dibujo a escala 1 cm a 10 m
de una cancha de f�tbol que tiene las medidas reglamentarias m�ximas. |
Completen la siguiente tabla para encontrar algunas de las
medidas de la cancha:
Recuerden que:
En el factor de escala las mismas
unidades se deben conservar. |
-
| a) |
�Cu�l es la constante de proporcionalidad que
permite pasar de una medida en el dibujo (en cent�metros) a su medida real (en
metros)? ___________________ |
-
| b) |
�Cu�l es el factor de escala? ___________________ |
-
| c) |
�Cu�ntas veces m�s grande es cada una de las
medidas de la cancha con respecto a su medida en el dibujo? ___________________ |
>>>Manos a la obra
-
 |
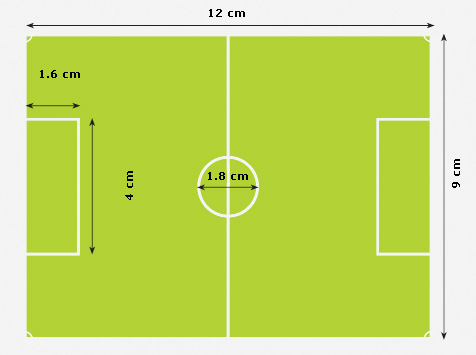
| I. |
Completen el siguiente esquema para
encontrar la medida real del largo de la cancha calculada en
cent�metros: |
|
|
|
|
Comenten |
�Cu�ntas veces m�s grande es la medida real del largo de la
cancha que su medida en el dibujo?
-
|
| II. |
Completen la siguiente tabla para
saber cu�ntas veces m�s grande es cada una de las medidas reales de la cancha
respecto a su medida en el dibujo. |
|
|
|
�Cu�l es el factor de escala que permite pasar de las medidas
en el dibujo (en cent�metros) a las medidas reales (en cent�metros)? _______________
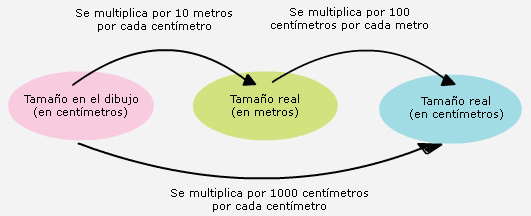
>>>A lo que llegamos
| En este problema, para
pasar de las medidas del dibujo a las medidas reales est�n involucradas varias
constantes de proporcionalidad: |
-
| 1. |
La constante de
proporcionalidad que permite pasar de las medidas de la cancha en el
dibujo (en cent�metros) a las medidas reales (en metros) es
10 metros por cada cent�metro. |
-
| 2. |
La constante de
proporcionalidad que permite pasar de las medidas reales (en metros) a las
medidas reales en (cent�metros) es 100 cent�metros por
cada metro.
Esta constante permite hacer el cambio de unidades de
metros a cent�metros. |
-
| 3. |
Finalmente, la constante de proporcionalidad que permite pasar de las
medidas de la cancha en el dibujo (en cent�metros) a las medidas reales (en
cent�metros) es 1 000 cent�metros por cada
cent�metro.
Este n�mero resulta ser el factor de escala. |
|
|
-
| III. |
En el dibujo de la cancha de f�tbol no
aparecen las medidas del �rea chica. Completen la siguiente tabla para
encontrar las dimensiones del �rea chica, de la porter�a y de la distancia que
hay entre la porter�a y el lugar donde se cobra un tiro penal. |
|
|
|
 |
-
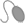| a) |
�Cu�l es la constante de proporcionalidad que
permite pasar de las medidas reales de la cancha (en metros) a la medida en el
dibujo (en cent�metros)? ___________________ |
-
| b) |
�Cu�ntas veces m�s chicas son las medidas del
dibujo con respecto de su medida real? ___________________ |
>>>A lo que llegamos
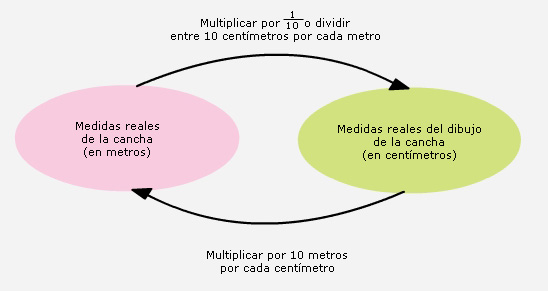
En este problema las
medidas del dibujo (en cent�metros) se pueden obtener multiplicando
 por las medidas reales (en metros). |
| La constante de proporcionalidad es
cent�metros por cada metro, y
permite pasar de cualquier medida real (en metros) a su medida en el dibujo (en
cent�metros). |
El siguiente esquema te ayudar� a comprender mejor la
explicaci�n anterior
