Secuencia�19Matem�ticas I
|
|
En esta secuencia construir�s tri�ngulos y
cuadril�teros, y analizar�s las
condiciones de existencia y unicidad. |
SESI�N 1
�EXISTE O NO EXISTE?
>>>Para empezar
Cuando se pide construir una figura geom�trica
con ciertas condiciones, a veces es posible hacerlo y a veces no. Por ejemplo,
�crees que sea posible trazar un tri�ngulo cuyos lados midan 10 cm, 1 cm y 1
cm?, �por qu�?
Este es el tipo de reflexiones que realizar�s
a lo largo de la secuencia. Es importante que hagas tus suposiciones o
hip�tesis y luego trates de comprobarlas.
>>>Consideremos lo siguiente
 |
Recorten popotes de las siguientes medidas. |
Traten de formar tri�ngulos, usando como
lados tres de los pedazos de popotes que cortaron. Completen la siguiente
tabla, anoten
 cuando sea posible formar el tri�ngulo.
cuando sea posible formar el tri�ngulo.
Medida de los popotes
para formar el tri�ngulo |
�Es posible formar el
tri�ngulo? |
| 8 cm, 3 cm, 2 cm |
|
| 8 cm, 6 cm, 4 cm |
|
| 8 cm, 4 cm, 2 cm |
|
| 6 cm, 4 cm, 3 cm |
|
| 6 cm, 3 cm, 2 cm |
|
-
| a) |
�Siempre fue posible construir tri�ngulos con las
tres longitudes?_________________________________ |
-
| b) |
Escriban tres longitudes de los popotes que no
est�n en la tabla con las que crean que s� es posible
construir un tri�ngulo
___________, ___________, ___________ |
-
| c) |
Escriban tres longitudes de los popotes que no
est�n en la tabla con las que crean que no es posible construir un tri�ngulo
___________, ___________,
___________ |
 |
Comenten sus hallazgos y resultados con sus
compa�eros de grupo. Expliquen cu�ndo creen que dadas tres longitudes es
posible construir un tri�ngulo y cu�ndo no es posible. |
>>>Manos a la obra
-
 |
| I. |
Recuerden c�mo se construye con
regla y comp�s un tri�ngulo si se conocen las medidas de sus lados. |
|
|
|
Construir un tri�ngulo cuyos lados midan 6 cm,
4 cm y 3 cm.Paso
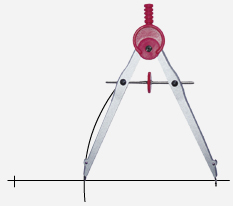
Paso 1. Se
traza un segmento de cualquiera de las medidas dadas, por ejemplo, 6 cm.
|
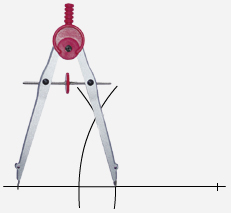
Paso 2. Se
abre el comp�s a cualquiera de las otras dos medidas y con centro en un extremo
del segmento, se traza un arco. |
|
|
|
Paso 3. Se
abre el comp�s a la tercera medida y con centro en el otro extremo del
segmento, se traza un arco que
cruce al anterior. |
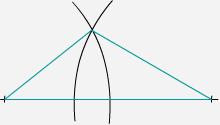
Paso 4.
Se unen los extremos del segmento con el punto donde se cortan los arcos y se
obtiene el tri�ngulo pedido. |
|
|
|
-
| II. |
Utilicen sus instrumentos geom�tricos para
trazar en su cuaderno tri�ngulos cuyos lados midan |
|
|
-
| III. |
Respondan las preguntas: |
|
|
-
| a) |
�Pudieron trazar los tres tri�ngulos?
______________________________________ |
-
| b) |
�Cu�l fue imposible trazar? _______________________________________ |
-
| c) |
Si dos lados de un tri�ngulo miden 6 cm y 3 cm,
indica una posible longitud para el tercer lado, de manera que se pueda trazar
el tri�ngulo. _______________________________________ |
-
| d) |
Tracen en su cuaderno tri�ngulos en los que dos
de sus lados midan 6 cm y 3 cm y el tercer lado tenga la longitud que ustedes
indiquen. |
-
| e) |
Si se pone la condici�n de que la medida del
tercer lado sea un n�mero entero, �cu�ntos tri�ngulos diferentes pueden
trazarse con dos lados que midan 6 cm y 3 cm? ___________________________________________ |
-
 |
| IV. |
Propongan tres medidas de
lados diferentes a las anteriores para que puedan trazar un tri�ngulo. |
|
|
|
-
| a) |
�Cu�les son esas medidas? _________�_________�
_________ |
-
| b) |
Tracen el tri�ngulo en su cuaderno y verifiquen
su hip�tesis; si no se puede trazar, intenten con otras medidas. |
-
 |
| V. |
Sin hacer trazos, anoten
 a los tri�ngulos que s� pueden trazarse. a los tri�ngulos que s� pueden trazarse. |
|
|
|
| Medida de los lados
|
�Existe el
tri�ngulo? |
| 10 cm, 5 cm, 5 cm |
|
| 8 cm, 9 cm, 2 cm |
|
| 1 cm, 0.5 cm, 2 cm |
|
| 2.5 cm, 3 cm, 1.5 cm |
|
4
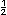 cm, 3 cm, 3
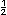 cm, 9 cm cm, 9 cm |
|
 |
Comenten sus respuestas con sus compa�eros de
grupo, traten de concluir qu� condici�n deben cumplir las tres medidas de los
lados de un tri�ngulo. |
>>>A lo que llegamos
| No siempre es posible construir un
tri�ngulo cuando se dan tres medidas de los lados, por ejemplo, no existe un
tri�ngulo cuyos lados midan 7cm, 4 cm y 2 cm |
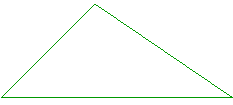
Para que el tri�ngulo exista, cada uno de
los lados debe ser menor que la suma de los otros dos. Por ejemplo, s� existe
un tri�ngulo cuyos lados midan 7cm, 4cm y 5cm, porque : |
 |
7 es menor que 4 + 5
4 es menor que 7
+ 5
5 es menor que 7 + 4 |
|
 |


 cuando sea posible formar el tri�ngulo.
cuando sea posible formar el tri�ngulo.

 a los tri�ngulos que s� pueden trazarse.
a los tri�ngulos que s� pueden trazarse.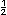 cm, 3
cm, 3
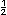 cm, 9 cm
cm, 9 cm