Anterior �ndice Siguiente

Secuencia�24Matem�ticas I

SESI�N 2

PROBABILIDAD CL�SICA

>>> Para empezar

En la sesi�n 4 de la secuencia 8, Problemas de conteo, trabajaron con un diagrama de �rbol para contar los resultados posibles al lanzar dos dados.

>>>Consideremos lo siguiente

El siguiente diagrama de �rbol muestra todos los resultados posibles que pueden obtenerse al lanzar dos dados.
  1. a) �Cu�ntos resultados diferentes en total puede haber al lanzar dos dados?_____________________________________________
  2. b) Si se hace referencia al evento “la suma de los puntos obtenidos en el lanzamiento de dos dados”, �qu� suma es m�s probable de obtener?__________________________________________________
  3. c) �Qu� suma tiene menos probabilidades de salir?_______________
  4. d) Si en un juego con dos dados te ofrecen la siguiente apuesta: “Si obtienes de tus dados una suma mayor a 7, ganas; si no, pierdes”, �te arriesgar�as a jugar? _____________�Por qu�?_______________
    �A qu� suma le apostar�as para tener m�s seguridad de ganar?
    ___________________________________________________
    �A qu� suma no le apostar�as?____________________________

>>>Manos a la obra

  1. a) Anota los resultados que faltan_____________________________
  2. b) �Cu�ntos resultados son?_________________________________
  3. c) Busca determinar qu� fracci�n del total de resultados representan___________________________________________
  4. d) �Cu�les son los resultados de: “obtener una suma igual a 12 al lanzar dos dados”? __________________________________________
  5. e) �Cu�ntos resultados son? ________________________________
  6. f) �Qu� fracci�n representan del total de resultados?______________
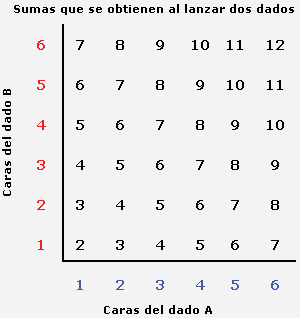
  7. g) Marquen en el siguiente diagrama los resultados favorables de: “obtener una suma igual a 7 al lanzar dos dados”.
  1. h) �Cu�ntos resultados son?________________________________
  2. i) �Qu� fracci�n representan del total de resultados?______________

>>>A lo que llegamos

Cuando se realiza un experimento aleatorio, el conjunto de todos los resultados sencillos posibles recibe el nombre de espacio de eventos o espacio muestral.
Por ejemplo, en el caso de lanzar dos dados, los resultados sencillos posibles son los que muestra el diagrama de �rbol y corresponden al espacio muestral de ese evento.
Si el evento es la suma que se obtiene al lanzar dos dados, el espacio muestral es el que se observa en el diagrama rectangular.
  1. j) Marquen en el mismo diagrama los resultados favorables del evento: “obtener una suma menor a 7”.
  2. k) �Cu�ntos resultados son?__________________________

>>>A lo que llegamos

Se llama probabilidad cl�sica de un evento al n�mero P(e) que se obtiene por medio del cociente:
P(e)=
Evento
(e)		 Resultados
(dado A, dado B)		 N�mero de
resultados favorables
al evento		 Probabilidad cl�sica
del evento P ( e )
La suma
de las caras de dos
dados al caer es mayor a 7 		(2,6), (3,5)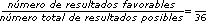
La suma de las
caras de dos
dados al caer es igual a 12
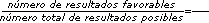La suma
de las caras de dos
dados al caer es igual a 7
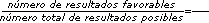La suma
de las caras de dos
dados al caer es menor a 12
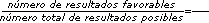La suma
de la cara de dos
dados al caer es menor a 7
  1. a) Consideren la probabilidad de los siguientes eventos:
    �Qu� evento es m�s probable que ocurra al lanzar dos dados: obtener una suma igual a 12 o una suma igual a 7?____________________________________
  2. b) �Qu� evento es m�s probable que ocurra al lanzar dos dados: obtener una suma mayor a 7 o una suma menor a 7?______________________________
  3. c) Calcula las siguientes probabilidades:
    P (La suma es igual a 1)=___________________
    P (La suma es igual a 6)=___________________
    �A qu� suma no le apostar�as?________________
  4. d) Completa la siguiente tabla calculando la probabilidad cl�sica de cada evento que se pide.
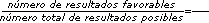Evento La suma es
igual a 13		 La suma es
un n�mero par		 La suma es
igual a 7		 La suma es
menor a 13
Probabilidad cl�sica
  1. e) �Cu�ntos resultados favorables existen al lanzar dos dados en los que la suma sea menor a 13?___________________________________
  2. f) �Cu�ntos resultados favorables existen al lanzar dos dados en los que la suma sea igual a 13?_____________________________________

>>>A lo que llegamos

Para obtener la probabilidad cl�sica de un evento no se requiere de la realizaci�n de experimentos, como en la probabilidad frecuencial, sino de conocer dos datos:
El de todos los resultados posibles que se pueden dar en una situaci�n de azar, y el de los resultados favorables de un evento de esa situaci�n:
P(e)=
A la probabilidad cl�sica se le llama tambi�n probabilidad te�rica. Cuando el n�mero de resultados favorables de un evento es el mismo que los resultados posibles (espacio muestral), se trata de un evento seguro, y la probabilidad de ese evento es igual a 1.
Cuando el n�mero de resultados favorables de un evento es 0, es decir, no hay casos favorables, entonces se trata de un evento imposible y la probabilidad de ese evento es 0.
Si el valor de la probabilidad de un evento es un n�mero muy cercano a 0, se dice que ese evento es poco probable, pero si el valor de la probabilidad de ese evento es un n�mero muy cercano a 1, entonces el evento es muy probable.

>>>Lo que aprendimos

  • 1. En una urna hay dos canicas blancas y dos negras. Extrae una canica de la urna, anota el color, y devu�lvela a la urna; de nuevo extrae una canica y anota su color. De esta forma, dos extracciones sucesivas conducen a uno de estos cuatro resultados:

�Cu�l es la probabilidad de cada uno de los siguientes eventos?

  1. a) Extraer dos canicas negras ______________________________
  2. b) Extraer dos canicas de diferente color ______________________
  3. c) Extraer dos canicas blancas______________________________