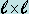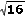Secuencia�26Matem�ticas I
|
|
Ra�z cuadrada y potencias
|
| En esta secuencia resolver�s problemas que
impliquen el c�lculo de la ra�z cuadrada y la potencia de exponente natural,
ambas de n�meros naturales y decimales. |
SESI�N 1
CUADROS Y M�S CUADROS
>>>Para empezar
 |
En la secuencia 4 de Matem�ticas encontraron la
expresi�n algebraica de la f�rmula del cuadrado. Si el lado del cuadrado mide
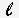 , entonces su �rea A se calcula con la expresi�n:
A = , entonces su �rea A se calcula con la expresi�n:
A =
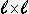 . En esta sesi�n, estudiar�n c�mo encontrar la medida
del lado del cuadrado a partir de su �rea. . En esta sesi�n, estudiar�n c�mo encontrar la medida
del lado del cuadrado a partir de su �rea. |
>>>Consideremos lo siguiente
 |
Calculen: |
-
| a) |
�Cu�l es el �rea de un cuadrado que tiene lados
que miden 2 cm? ___________________________________________________ |
-
| b) |
�Cu�l es el �rea de un cuadrado que tiene lados
que miden 3 cm?___________________________________________________ |
-
| c) |
�Cu�nto mide el lado de un cuadrado que tiene 16
cm2 de �rea?___________________________________________________ |
-
| d) |
�Cu�nto mide el lado de un cuadrado que tiene 25
cm2 de �rea?___________________________________________________ |
-
| e) |
�Creen que exista alg�n cuadrado de 18 cm2 de
�rea?__________ �Cu�nto medir�an sus lados?_______________ |
Expliquen y comprueben sus respuestas en su
cuaderno.
 |
Comparen sus respuestas. |
>>>Manos a la obra
-
 |
| I. |
En la ilustraci�n hay un cuadrado
blanco cuyos lados miden 6 cm, dentro del cuadrado blanco hay un cuadrado azul.
Contesten las siguientes preguntas: |
|
|
|
-
| a) |
Calculen el �rea del cuadrado blanco_______________ |
Tracen las diagonales del cuadrado azul. Van a
obtener cuatro tri�ngulos azules iguales.
-
| b) |
Calculen el �rea de cada tri�ngulo azul
_______________ |
-
| c) |
Calculen el �rea del cuadrado azul
______________________ |
-
| d) |
�Cu�nto miden los lados del cuadrado azul?_______________ |
Midan con su regla.
-
| e) |
En sus cuadernos, comprueben la medida que
obtuvieron para el lado del cuadrado azul aplicando la f�rmula del �rea: A = 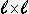 |
�Qu� valor del �rea encontraron usando la
f�rmula?_______________
Recuerden
que: El �rea de un tri�ngulo con medida de la altura a y medida de la base
b se calcula: A =
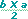 |
 |
Comparen sus respuestas y comenten: |
-
| a) |
De los valores del �rea que encontraron usando
la f�rmula, �cu�l es el que m�s se aproxima a 18 cm2? |
-
| b) |
�Cu�l es la mejor aproximaci�n que encontraron
para la medida del lado del cuadrado? |
-
 |
| II. |
Llenen la siguiente tabla para
encontrar valores aproximados a la medida del lado del cuadrado de �rea 18
cm2
|
|
|
|
-
| a) |
�Cu�l es el valor m�s aproximado que encontraron
para la medida del lado del cuadrado?_____________________________________________ |
-
| b) |
�Podr�an encontrar un valor m�s aproximado?
____________________
�Cu�l?_______________ |
 |
Comparen sus respuestas. |
-
 |
| III. |
�Creen que exista alg�n cuadrado
de 32 cm2 de �rea? _______________
�Cu�nto
medir�an sus lados? _______________ |
|
|
|
-
| a) |
Completen la siguiente tabla para encontrar
valores aproximados a la medida de sus lados. |
-
| b) |
La medida del lado de este cuadrado est� entre
5.6 cm y 5.7 cm. �Con qu� valor continuar�an la tabla para encontrar un valor
que se aproxime m�s a la medida del lado de este cuadrado?_______________ |
-
| c) |
Hagan la comprobaci�n. �Qu� valor del �rea
encontraron?_____ |
 |
Comparen sus respuestas y hagan la
comprobaci�n. |
>>>A lo que llegamos
- Para calcular el �rea de un cuadrado, conociendo
la medida de su lado
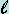 , se multiplica la medida del lado por ella
misma: , se multiplica la medida del lado por ella
misma:
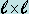 . .
En general, cuando se multiplica un n�mero
por �l mismo, por ejemplo y � y, se dice que se
calcula la segunda potencia o el
cuadrado del n�mero. Esto se escribe:
y2
.
Por ejemplo, al calcular 5 � 5 , se
dice que se est� calculando 5 a la
segunda potencia o el cuadrado de 5, y se escribe
52
. O sea:
5 � 5 =
52 = 25.
- Al calcular el lado de un cuadrado a partir de su
�rea se dice que se calcula la ra�z cuadrada del
�rea. En general, la ra�z cuadrada de un n�mero
A es el n�mero que multiplicado por �l mismo da
A.
Por ejemplo, la ra�z cuadrada de
16 es 4, porque
4 � 4 = 16. La ra�z cuadrada de
16 se escribe:
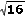
|
-
 |
| IV. |
Llenen la siguiente tabla: |
|
|
|
|
|
| Pueden usar calculadora para hacer
y verificar sus c�lculos. |
|
A partir de la informaci�n de la tabla anterior, relacionen las dos columnas:
 |
Comparen sus respuestas y hagan las
comprobaciones. |
>>>A lo que llegamos
El cuadrado de un n�mero y la ra�z
cuadrada son operaciones inversas. Esto quiere
decir que si a un n�mero se le aplica una operaci�n y despu�s la otra, se
obtendr� el n�mero original.
Por ejemplo, el cuadrado del n�mero 15 es: 152
= 15 �
15 = 225. Y la
ra�z cuadrada del n�mero 225 es:
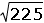 = 15. = 15. |
>>>Lo que aprendimos
 |
-
| 1. |
En tu cuaderno encuentra una
aproximaci�n para la medida del lado de un cuadrado de �rea 2 cm2.
|
-
| 2. |
Relaciona las dos columnas. |
|
(a) �Cu�l es el �rea del cuadrado
cuyos
lados miden 10 cm? |
( ) 196 |
| (b) �Cu�l es la ra�z cuadrada de
196? |
( ) 100 cm2
|
| (c) �Cu�nto es 142? |
( ) 11.5 |
(d) �Cu�nto es
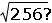 ? ? |
( ) 16 |
(e) �Cu�l es el �rea de un cuadrado
cuyos
lados miden 7 cm? |
( ) 49 cm2
|
(f) �Cu�nto es
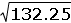 ? ? |
( ) 14 |

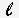 , entonces su �rea A se calcula con la expresi�n:
A =
, entonces su �rea A se calcula con la expresi�n:
A =
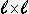 . En esta sesi�n, estudiar�n c�mo encontrar la medida
del lado del cuadrado a partir de su �rea.
. En esta sesi�n, estudiar�n c�mo encontrar la medida
del lado del cuadrado a partir de su �rea.



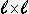
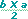







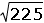 = 15.
= 15. 
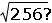 ?
?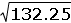 ?
?