Secuencia�28Matem�ticas I
|
|
SESI�N 2
CUERDAS Y CIRCUNFERENCIAS
>>>Para empezar
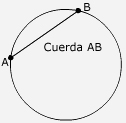
Los segmentos de recta que unen a dos puntos de
una circunferencia se llaman cuerdas. En la
ilustraci�n 1 los puntos A y B est�n unidos por la cuerda AB.
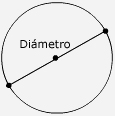
El di�metro de una circunferencia es una cuerda
que pasa por el centro de la circunferencia.
>>>Consideremos lo siguiente
Una maquiladora de latas de refresco debe
colocar la “leng�eta” exactamente en el centro de la tapa. En el
dibujo se muestra una tapa sin la leng�eta, las l�neas sirven de gu�a para
poner la leng�eta y son dos cuerdas de la circunferencia.
 |
Encuentren el punto de la tapa donde debe
colocarse el remache de la leng�eta. |
>>>Manos a la obra
-
| I. |
Veamos dos procedimientos: |
|
|
Procedimiento 1
-
 |
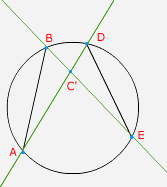
En el equipo 1 unieron los extremos de las cuerdas y
tomaron como centro de la tapa el punto de intersecci�n C’. Dijeron que
el remache de la leng�eta deber�a colocarse en el punto C’. |
Procedimiento 2
-
 |
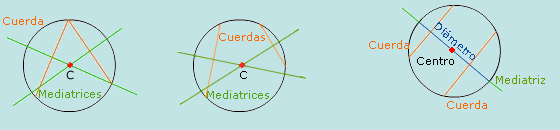
En el equipo 2 trazaron las mediatrices de la
cuerdas y dicen que el punto de intersecci�n de las mediatrices es donde debe
ponerse el remache de la leng�eta. |
|
|
-
| a) |
�Cu�nto miden las distancias del punto C’
a los extremos de cada cuerda? M�danlas y completen: |
| Distancia de C’ a A |
__________ |
Distancia de C’ a B |
__________ |
| Distancia de C’ a D |
__________ |
Distancia de C’ a E |
__________ |
-
| b) |
�Cu�nto miden las distancias del punto C a los
extremos de cada cuerda? Completen: |
| Distancia de C a A |
__________ |
Distancia de C a B |
__________ |
| Distancia de C a D |
__________ |
Distancia de C a E |
__________ |
 |
Comparen sus respuestas y comenten: |
-
 |
�Por qu� el punto C’ no
es el centro de la circunferencia? |
-
 |
�Por qu� el punto de intersecci�n C de las dos
mediatrices s� es el centro de la circunferencia? |
 |
-
| II. |
En las siguientes circunferencias: |
|
|
|
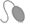 |
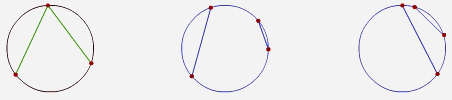 |
| Circunferencia 1 |
Circunferencia 2 |
Circunferencia 3 |
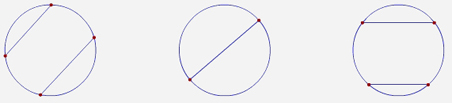 |
| Circunferencia 4 |
Circunferencia 5 |
Circunferencia 6 |
-
| c) |
En la circunferencia 5 la cuerda dada es un
di�metro, �c�mo obtuvieron su centro?_____________________________________________ |
-
| d) |
En las circunferencias 4 y 6, �las mediatrices de
las cuerdas se intersectan en un punto, son la misma recta o son rectas
paralelas?_____________________________________________________ |
-
| e) |
La mediatriz que trazaron corta a la
circunferencia 4 en dos puntos, ll�menlos A y B; obtengan el punto medio de la
cuerda AB y ll�menlo D. |
-
| f) |
�C�mo son las distancias del punto D a cada
extremo de la cuerda AB? M�danlas y completen: |
| Distancia de D a A_____________ |
Distancia de D a B_____________ |
 |
Comparen sus respuestas y comenten: |
-
 |
�Por qu� la cuerda AB es un di�metro de la
circunferencia 4? |
-
 |
�Por qu� el punto D es el centro de la circunferencia
4? |
-
 |
�Con este procedimiento podr�n encontrar el centro de
la circunferencia 6? H�ganlo. |
>>>A lo que llegamos
| Para encontrar el centro de las
circunferencias dadas: |
| a) Dos cuerdas no
paralelas, se traza la mediatriz a cada cuerda y el punto de intersecci�n
de las mediatrices trazadas es el centro de la circunferencia. |
b) Dos cuerdas
paralelas, se traza la mediatriz a una de las cuerdas, se identifica el
di�metro que est� sobre la mediatriz, se obtiene el punto medio del di�metro,
el cual es el centro de la circunferencia. |
 |