Secuencia�28Matem�ticas I
|
|
SESI�N 3
TRES PUNTOS Y UNA CIRCUNFERENCIA
>>>Para empezar
 |
En la primera sesi�n de esta secuencia estudiaron
c�mo trazar circunferencias que pasen por dos puntos dados. En la segunda
sesi�n estudiaron c�mo obtener el centro de una circunferencia dadas dos
cuerdas. En esta sesi�n aprender�n c�mo trazar una circunferencia que pase por
tres puntos dados. |
>>>Consideremos lo siguiente
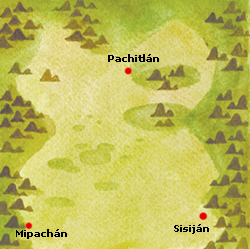
La siguiente ilustraci�n indica
los lugares en que se ubican las comunidades de Pochitl�n, Mipach�n y
Sisij�n.
 |
Se quiere construir un centro de salud que est�
a la misma distancia de todas ellas. Encuentren el sitio donde se deber�a
construir ese centro de salud. |
>>>Manos a la obra
-
 |
| I. |
A continuaci�n se explica una
manera de encontrar un punto que equidiste de los tres pueblos. |
|
|
|
-
| a) |
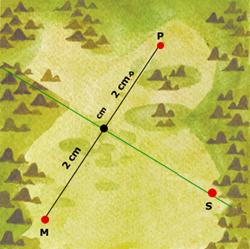
En el siguiente dibujo los pueblos se
representan con puntos. Ya se traz� la mediatriz del
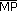 . La distancia del punto M al punto C
(cualquier punto de la mediatriz) es la misma que la distancia del punto P al
mismo punto C. . La distancia del punto M al punto C
(cualquier punto de la mediatriz) es la misma que la distancia del punto P al
mismo punto C. |
-
| b) |
Tracen la mediatriz de
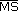 y y
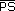 . . |
-
| c) |
Localicen el punto de intersecci�n de las
mediatrices y ll�menlo D. Midan la distancia de D a cada uno de los pueblos: |
Distancia de D a M: ________________
Distancia de D
a P: ________________
Distancia de D a S:
________________ |
Recuerden
que:
El conjunto de puntos que equidistan de los extremos de un
segmento forman una recta llamada mediatriz del segmento. |
|
 |
Comparen sus resultados y comenten: |
-
| a) |
�Es conveniente construir el centro de salud en
el punto D? |
-
| b) |
�Para encontrar un punto que equidiste de los
puntos M, P y S ser� necesario trazar las tres mediatrices o ser� suficiente
con trazar dos de ellas? |
 |
En el siguiente dibujo tracen dos de las tres
mediatrices |
-
| a) |
Llamen F al punto de intersecci�n de las dos
mediatrices. |
-
| b) |
�Cu�les son las distancias del punto F a los
puntos A, B y C?
Distancia de F a A: ________________________________
Distancia de F a B: ________________________________
Distancia de F a C:________________________________ |
-
 |
| II. |
En la siguiente ilustraci�n se
muestran los lugares en donde se ubican otras tres comunidades: D, E y F.
Encuentren un punto que est� a la misma distancia de los tres pueblos. |
|
|
|
| Cuando tres puntos est�n en una
misma recta se dice que son colineales. |
-
| a) |
Unan los puntos mediante segmentos. |
-
| b) |
Tracen las mediatrices de los segmentos. |
-
| c) |
Encuentren la intersecci�n de las mediatrices.
|
 |
Comenten: |
-
| a) |
Estos tres puntos est�n en una misma recta, �por
qu� creen que no se intersectan las mediatrices de los segmentos que los
unen? |
-
| b) |
�En qu� lugar creen que ser�a m�s conveniente
construir un centro de salud? |
-
 |
| III. |
En sus cuadernos dibujen tres
puntos, los que quieran, pero que no sean colineales.
Tracen una circunferencia
que pase por los tres puntos que dibujaron. |
|
|
|
 |
Comparen los puntos que dibujaron y las
circunferencias que trazaron. Comenten:
Dados tres puntos, �se podr� siempre
trazar una circunferencia que pase por ellos? |
>>>A lo que llegamos
- Dados tres puntos que no son
colineales siempre se puede trazar una circunferencia que pase por ellos.
El centro de la circunferencia que pasa por ellos es el punto de intersecci�n
de las mediatrices de
 y y
 . .
- Cuando los tres puntos son
colineales (est�n sobre la misma recta), no se puede trazar la
circunferencia.
|
>>>Lo que aprendimos

 |
-
| 1. |
En los siguientes casos, tracen una
circunferencia que pase por los tres puntos. |
|
-
| a) |
�En cu�les de los tres casos pudieron trazar una
circunferencia? _______________________________________________________
_______________________________________________________
�Por qu�?________________________________________________ |
>>>Para saber m�s
 |
Sobre c�rculo, circunferencia, puntos
colineales, di�metro y radio consulta:
http://www.sectormatematica.cl/geometria.htm (fecha de
consulta 23 de junio 2006) Sector Matem�tica.
Ruta: ENLACE NB6 (13 A�OS)
 GEOMETR�A GEOMETR�A
 DEFINICIONES DEFINICIONES
 dar clic en la definici�n que quieran ver a
detalle. dar clic en la definici�n que quieran ver a
detalle. |
 |
 |
Sobre c�rculo y circunferencia consulta en las Bibliotecas
Escolares y de Aula: De la Pe�a, Jos� Antonio (2002). Geometr�a y el mundo. M�xico: SEP/Santillana (Colecci�n
Biblioteca Juvenil Ilustrada), Libros del Rinc�n. Hern�ndez, Carlos (2002).
La geometr�a en el deporte. M�xico: SEP/Santillana
(Colecci�n Biblioteca Juvenil Ilustrada), Libros del Rinc�n. |



 . La distancia del punto M al punto C
(cualquier punto de la mediatriz) es la misma que la distancia del punto P al
mismo punto C.
. La distancia del punto M al punto C
(cualquier punto de la mediatriz) es la misma que la distancia del punto P al
mismo punto C.  y
y
 .
. 








 GEOMETR�A
GEOMETR�A
 DEFINICIONES
DEFINICIONES
 dar clic en la definici�n que quieran ver a
detalle.
dar clic en la definici�n que quieran ver a
detalle. 





