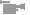Secuencia�36Matem�ticas I

Gr�ficas, tablas y expresiones algebraicas

En esta secuencia aprender�s a calcular valores faltantes a partir de varias representaciones (gr�ficas, tabulares y algebraicas), relacionando las representaciones que corresponden a la misma situaci�n, e identificando aquellas que son de proporcionalidad directa.

SESI�N 1

GR�FICAS, TABLAS Y EXPRESIONES ALGEBRAICAS ASOCIADAS A PROBLEMAS DE PROPORCIONALIDAD DIRECTA

>>>Para empezar

Elementos de la proporcionalidad directa

Como han aprendido en las secuencias 31 y 32 de su libro de Matem�ticas I, los problemas en los cuales est�n involucradas cantidades directamente proporcionales tienen los siguientes tres elementos a tomar en cuenta para su resoluci�n.

La tabla.
La expresi�n algebraica.
La gr�fica.

A lo largo de esta secuencia estudiar�n c�mo usar estos tres elementos de distintas formas para resolver problemas de cantidades directamente proporcionales.

>>>Consideremos lo siguiente

Consideren la expresi�n algebraica:

y = 2x

�Cu�l o cu�les de las siguientes situaciones tienen asociada la expresi�n algebraica anterior? Justifiquen sus respuestas.

Recuerden que: El tipo de cambio de francos franceses a pesos mexicanos es la cantidad de pesos mexicanos que se obtienen al cambiar un franco franc�s.

a)	El tipo de cambio de francos franceses a pesos mexicanos, si por cada franco franc�s se obtienen dos pesos mexicanos.

b)	Las edades de Juan y Laura si se sabe que cuando Juan cumpla diecis�is a�os, tendr� dos veces la cantidad de a�os que tendr� Laura.

c) El costo de cierto n�mero de llamadas si cada llamada cuesta dos pesos.

d)	El tipo de cambio de pesos uruguayos a pesos mexicanos, si por cada dos pesos uruguayos se obtiene un peso mexicano.

>>> Manos a la obra

I.	Encuentren la expresi�n algebraica que permite calcular la cantidad de pesos que se obtienen al cambiar determinada cantidad de francos, es decir, el tipo de cambio de francos a pesos (situaci�n del inciso a).

Representen con la letra x la cantidad de francos que se van a cambiar y con la letra y la cantidad de pesos que se obtienen al cambiar los francos. ________________________________________________________

Encuentren la expresi�n algebraica asociada al aumento de las edades de Juan y Laura. Representen con la letra u la cantidad de a�os que tiene Laura y con la letra v la cantidad de a�os que tiene Juan (situaci�n del inciso b). ________________________________________________________

Comparen sus expresiones y comenten c�mo las encontraron.

II.	Completen las siguientes tablas para establecer cu�l de las dos situaciones anteriores es de proporcionalidad directa.

Recuerden que: Dos cantidades est�n en proporci�n directa si al aumentar una (al doble, triple, etc.), o al disminuir (a la mitad, la tercera parte, etc.), la otra aumenta (al doble, triple, etc.), o disminuye (a la mitad, tercera parte, etc.)

�Cu�l de las tablas anteriores es de proporcionalidad directa?

III.	Con la informaci�n de las tablas anteriores completen las siguientes gr�ficas.

IV.	En sus cuadernos encuentren las expresiones, hagan las tablas y las gr�ficas correspondientes a las relaciones de los incisos c) y d) para determinar si las situaciones tienen asociada la expresi�n algebraica del inicio de la sesi�n.

>>>A lo que llegamos

Para determinar si una situaci�n es de proporcionalidad directa se puede hacer lo siguiente:

A partir de la situaci�n, construir una tabla para encontrar algunos valores y determinar si esta tabla es de proporcionalidad directa.
A partir de la tabla, construir la gr�fica y determinar si los puntos est�n en una l�nea recta que pasa por el origen.
Encontrar la expresi�n algebraica asociada a la situaci�n y determinar si es de la forma y = kx, donde k es la constante de proporcionalidad.

Puede suceder que distintas situaciones proporcionales tengan la misma expresi�n algebraica asociada. Por ejemplo, dos de las situaciones de proporcionalidad de esta secuencia son distintas, pero tienen asociada la misma expresi�n algebraica: y = 2x

>>>Lo que aprendimos

1. Considera la siguiente expresi�n algebraica:

y = 3x

�Cu�l o cu�les de las siguientes situaciones tienen asociada la expresi�n algebraica anterior? Justifica tu respuesta.

a)	Las ganancias en t�rminos de la cantidad de dinero invertido, si se sabe que por cada dos pesos invertidos se ganan tres pesos.

b) Las velocidades de dos autom�viles si uno va al triple de velocidad que el otro.
c) Una m�quina produce una lata cada tres segundos. �Cu�ntas latas producir� en x segundos?