Propósito de la sesión. Identificar las propiedades de los sistemas de numeración aditivos no posicionales, mediante el sistema de numeración egipcio. Organización del grupo. Gran parte del trabajo en la sesión es en parejas, excepto en los momentos de intercambio grupal y en Lo que aprendimos, en donde es individual.

Eje

Sentido numérico y pensamiento algebraico.

Tema

Significado y uso de los números.

Antecedentes

Durante la escuela primaria los alumnos reflexionaron sobre las reglas del sistema de numeración decimal, particularmente sobre el agrupamiento y el valor posicional a través de actividades de lectura, escritura, ordenamiento y construcción de series numéricas con números naturales. Ahora se pretende que se hagan explícitas las ventajas del sistema decimal comparándolo con otros sistemas posicionales y no posicionales.

Propósitos de la secuencia Identificar las propiedades del sistema de numeración decimal y contrastarlas con las de otros sistemas numéricos posicionales y no posicionales.
Sesión	Propósitos de la sesión	Recursos
1	Acertijos arqueológicos Identificar las propiedades de los sistemas de numeración aditivos no posicionales, mediante el sistema de numeración egipcio.
2	Otro sistema de numeración Identificar las propiedades de los sistemas de numeración posicionales, mediante el sistema de numeración maya.	Video "Los números mayas" Interactivo
3	El sistema decimal Explicitar las principales características del sistema de numeración decimal.

Sugerencia didáctica. Comente con los alumnos que en esta primera secuencia se incluyen breves comentarios sobre lo que se va a hacer en cada apartado y sobre la forma de organizarse para trabajar.

Sugerencia didáctica.Es importante que los alumnos se enfrenten a la actividad por sí mismos, así que en este momento es preferible no darles explicaciones sobre las respuestas o los procedimientos que pueden utilizar. Respuestas. En el sistema de numeración egipcio cada símbolo tiene un valor independientemente del lugar en el que se coloque, por ello se dice que es un sistema no posicional. Para representar el número 8 se escriben ocho símbolos de valor 1, para representar el 76 se escriben siete símbolos de valor 10 y seis de valor 1.

Sugerencia didáctica.Cuando los alumnos lleguen a este punto de la tabla todavía no conocerán el símbolo que vale 10 000. Si tienen dificultades sugiérales que sigan adelante, ya que en el siguiente cuadro tendrán manera de saber el valor de dicho símbolo. Lo mismo ocurre en el cuadro en el que hay que escribir con símbolos egipcios el número 1 200 108

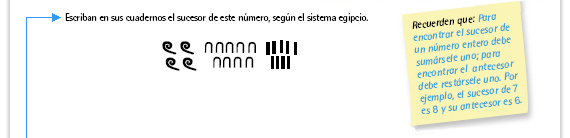
Posibles procedimientos. Hay dos maneras de resolverlo. La más directa es traducir el número al sistema decimal. Si se escribe el número 499, el sucesor es el 500 y se escribe con 5 símbolos de 100. Otra forma es agregando un símbolo de valor 1, pero entonces se tendrán 10 símbolos de 1 que se cambian por uno de 10; y también se tendrán 10 de 10, por lo que habrá que cambiarlos por uno de 100. Es posible que algunos alumnos nada más agreguen un símbolo de uno y no se den cuenta de que deben efectuar cambios. Puede retomarlo en la discusión grupal, para que se den cuenta del agrupamiento.

Sugerencia didáctica. No es necesario que pasen todos los alumnos ni todos los equipos a explicar sus respuestas porque puede volverse tedioso para el resto del grupo. Pida a algunos alumnos que pasen al pizarrón a escribir sus respuestas y pregunte a los demás si alguien lo hizo diferente o si obtuvo otro resultado. Es posible que durante el intercambio los alumnos vayan comprendiendo las reglas del sistema de numeración egipcio. Recupérelas sin dar aún explicaciones.

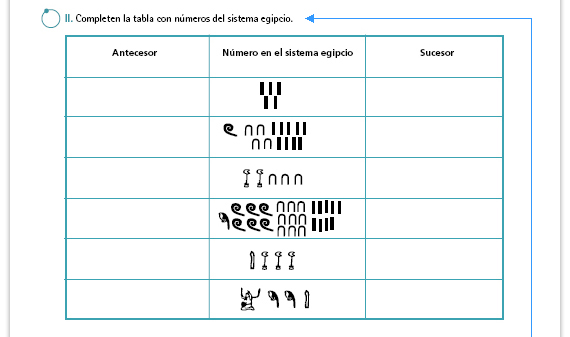
Propósito de la actividad. Interesa que al escribir el antecesor y el sucesor de un número los alumnos trabajen haciendo agrupamientos y desagrupamientos en un sistema no posicional, por ello es importante que intenten resolverlo sin escribirlos en el sistema decimal. Escribir el antecesor de ciertos números puede ser especialmente laborioso por la gran cantidad de símbolos que hay que emplear, anime a los alumnos a hacerlo porque tendrán más elementos para comparar al sistema egipcio con el decimal y reconocer las ventajas de este último.

Respuestas. Se necesitan 9 símbolos de cada valor: 9 de 10 000, 9 de 1 000, 9 de 100, 9 de 10 y 9 de 1; 45 en total. Posibles procedimientos. Una manera de contestar la pregunta es escribiendo con símbolos egipcios el número que se solicita (el 99 999). También pueden analizar mentalmente el número sin necesidad de escribirlo: el 99 999 necesita 9 símbolos de 10 000, 9 de 1 000, 9 de 100, 9 de 10 y 9 de 1. En total son 45.

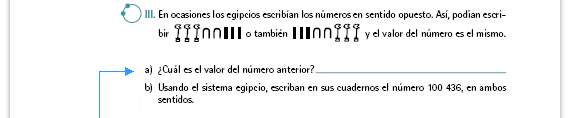
Respuestas. a) El número es 3 024, no importa el orden en el que se escriban los símbolos. b) Se necesita Sugerencia didáctica.Puede preguntar a los alumnos si existe en el sistema egipcio un símbolo para el cero. Si ya se dieron cuenta de que no lo hay, pregúnteles si consideran pertinente que lo hubiera y por qué.

Sugerencia didáctica. Puede preguntar al grupo cómo escribirían 250 millones (se requieren 250 símbolos de millón o tener un símbolo para 10 millones y uno para 100 millones).

Sugerencia didáctica. Pregunte a los alumnos si encuentran otras desventajas del sistema egipcio, por ejemplo, que es tardado hacer cada uno de los dibujos.

Posibles procedimientos. Hay dos maneras de resolver la actividad: haciendo las sumas de símbolos egipcios y los agrupamientos necesarios, o bien escribir cada número en el sistema decimal, realizar la suma y luego pasar el resultado al sistema egipcio. Integrar al portafolios. Solicite a los alumnos que en clase o como tarea, resuelvan esta actividad en una hoja aparte para que pueda integrarla al portafolios. Si los alumnos tienen dificultades al resolverla es conveniente repasar juntos la sección Manos a la obra de esta sesión.