
|

|

|
 |
 |

| Propósito de la sesión. Interpretar
procedimientos sistemáticos de conteo.
Organización del grupo. Se recomienda que la primera parte de la sesión se resuelva de manera individual, y que el resto se trabaje en parejas. |
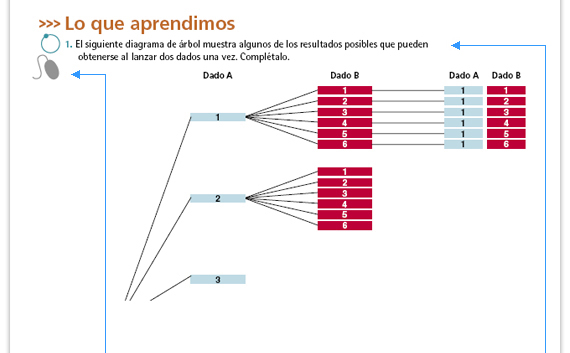
| Propósitos del interactivo: Utilizar el diagrama de árbol como técnica de conteo en la resolución de problemas. |  Para responder a las preguntas de
esta actividad, los alumnos requieren
analizar la información que se muestra
en el diagrama; por ello es conveniente
que antes de que resuelvan de manera
individual, comenten grupalmente
cómo interpretan el diagrama en
términos generales: cuántos niveles
tiene, qué se representa en cada nivel
y qué se representa en las ramas.
Para responder a las preguntas de
esta actividad, los alumnos requieren
analizar la información que se muestra
en el diagrama; por ello es conveniente
que antes de que resuelvan de manera
individual, comenten grupalmente
cómo interpretan el diagrama en
términos generales: cuántos niveles
tiene, qué se representa en cada nivel
y qué se representa en las ramas. |
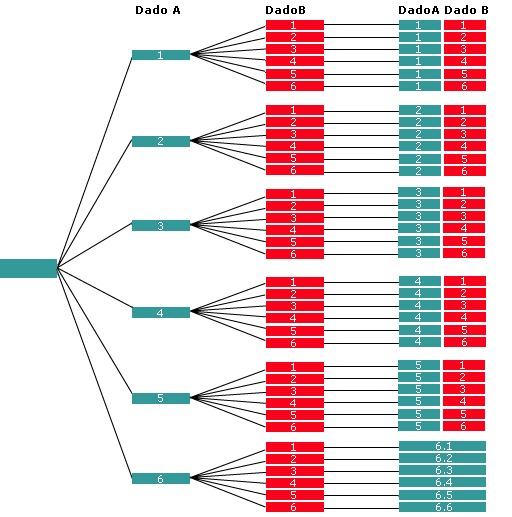

Respuestas:
|
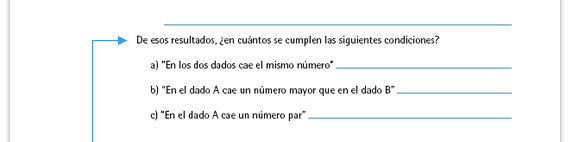
Respuestas:
Sugerencia didáctica. Usted puede retomar estas preguntas para destacar las relaciones entre algunos de los datos; por ejemplo, en los incisos b y c se generalizan las respuestas que obtuvieron para los incisos a, b y c, de la actividad anterior. |

Respuestas:
|

| Propósito de la actividad. Utilizar
la información que proporciona el
diagrama de árbol para producir otra
información (por ejemplo, la suma de
los resultados de ambos números).
Posibles dificultades. Esta actividad se ubica en el contexto de juegos de azar; si bien no es propósito de esta sesión que los alumnos resuelvan situaciones de probabilidad, sí es importante destacar que algunas de las dificultades que podrían tener son:
En caso de que se presente alguna de las dificultades anteriores, invite a los alumnos a revisar nuevamente el diagrama de árbol para identificar los diferentes resultados que pueden obtenerse. Respuestas:
|

| Respuesta. En todos los resultados el dado A cayó en 4. |

Respuestas:
|

| Integrar al portafolios. Si los
alumnos tuvieron dificultades para
resolver el problema, resuélvalo
nuevamente junto con ellos haciendo
un diagrama de árbol y analizándolo
de acuerdo con las preguntas que se
plantean en esta misma actividad.
Si algún alumno encontró alguna
operación con la cual se puede
encontrar el número total de claves
que se pueden formar, pídale que
la explique. Si nadie tiene alguna
operación que proponer, entonces con
ayuda del diagrama de árbol pueden
observar que hay cuatro opciones
para la primera cifra (2, 3, 4 y 5), en
la segunda cifra hay dos opciones (0
y 1) y, finalmente, en la tercera cifra
hay otras cuatro opciones (6, 7, 8
y 9), por lo que el número total de
claves se puede obtener mediante la
operación 4 × 2 × 4. Como ve, este
problema permite que los alumnos
lo aborden utilizando alguno de los
procedimientos que se estudiaron en
esta secuencia, lo que nos permite
obtener información sobre el nivel
de razonamiento combinatorio que
tienen.
Respuestas:
|