Propósito de la sesión. Encontrar procedimientos sistemáticos de conteo en situaciones diversas; particularmente utilizar la regla del producto. Organización del grupo. Se recomienda que organice al grupo en parejas para trabajar de esa manera durante toda la sesión.

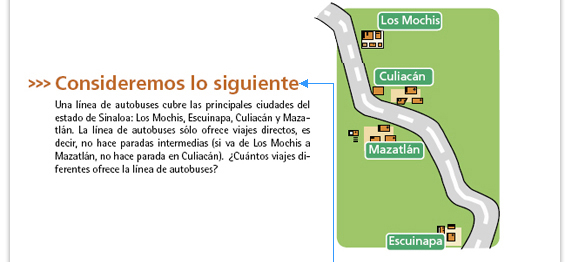
Posibles procedimientos. En las lecciones anteriores los alumnos han utilizado distintas estrategias para contar los resultados, particularmente se ha tratado de propiciar el uso del diagrama de árbol, las tablas o algún código. Se espera que los alumnos utilicen cualquiera de esas estrategias para la resolución de este problema; no obstante, podrían utilizar otras, por ejemplo, apoyándose en el mapa, podrían empezar a contar de la siguiente manera. Los Mochis- Culiacán, Los Mochis-Mazatlán, Los Mochis-Escuinapa, etcétera. El reto con esta estrategia es que logren tener un control que les permita cubrir todos los recorridos posibles y evitar repeticiones.

Propósito de las actividades. Estas preguntas ayudarán a los alumnos a comprender y explorar mejor el problema inicial; particularmente si algunos alumnos proponen que un viaje sea Los Mochis-Culiacán- Mazatlán; al organizar la información en la tabla podrán percatarse de que únicamente deben considerar el lugar de salida y el de llegada del viaje. Respuestas. b) 3 c) 3 d) Son 12 viajes diferentes: de cada cuidad se puede ir a 3 destinos, hay 4 ciudades (4 × 3).

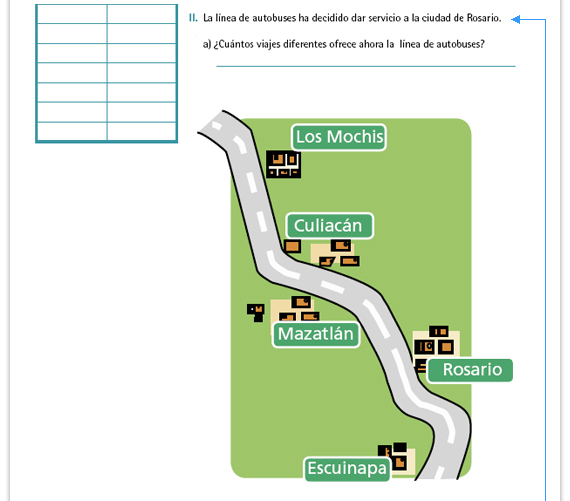
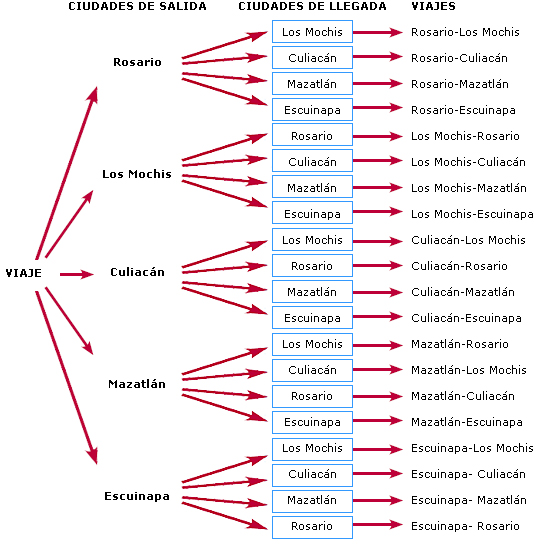
Propósito de la actividad. Si en la primera parte de la lección los alumnos no utilizaron como procedimiento de resolución un diagrama de árbol o una tabla, en esta parte se les pide que empleen y analicen un diagrama de árbol. Este diagrama puede ser creado en el applet o en el cuaderno. Respuesta. Son 5 ciudades de salida, cada una tiene 4 ciudades posibles de llegada, en total hay 20 viajes.

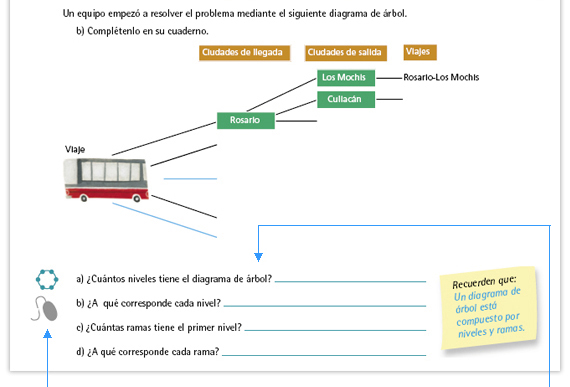
Propósito del interactivo. Utilizar el diagrama de árbol como técnica de conteo en la resolución de problemas.

Propósito de la actividad. Con este conjunto de preguntas se pretende que los alumnos conozcan y analicen un procedimiento más económico y eficiente que les ayude a encontrar la respuesta al problema; se trata de la regla del producto, que en este caso es la multiplicación del número de ciudades de salida por el número de ciudades de llegada Respuestas. a) 3 niveles; b Ciudades de salida, Ciudades de llegada, Viajes; c) 20 ramas; d) A una ciudad de llegada; e) 20 ramas; f) Cada rama corresponde a un viaje; g) 4 opciones de viaje; h) 20 opciones de viaje; i) El número de ciudades de salida (5) por el número de ciudades de llegada (4), es igual al número total de viajes: 5 × 4 = 20.

Sugerencia didáctica. Invite a los alumnos a utilizar la regla anterior ("número de ciudades de salida por número de ciudades de llegada") para responder a estas preguntas. Respuestas. El inciso a se obtiene multiplicando 6 × 5; en el inciso b se multiplica 10 × 9, y en el inciso c, 32 × 31.

Propósito de la información. Los alumnos cuentan al menos con tres procedimientos sistemáticos para resolver problemas que implican conteos: diagrama de árbol, tablas y multiplicación. Se espera que logren identificarlos como recursos que les permiten resolver ese tipo de problemas y que puedan elegir la utilización de uno o de otro.

Integrar al portafolios. Pida a los alumnos que en la hoja en la que entregarán el ejercicio, incluyan los procedimientos o los recursos que hayan utilizado para resolver el problema (cálculos, tablas, diagramas de árbol o cualquier otro recurso). Para poder aplicar adecuadamente la regla del producto, los alumnos deben identificar la cantidad de números que pueden utilizar en cada cifra. Tal vez algunos alumnos tengan dificultades para plantear la multiplicación y les resulte más claro elaborar una tabla o un diagrama. En general, algunas de las dificultades que los alumnos suelen tener al resolver problemas de conteo están relacionadas con el número de elementos de cada conjunto o grupo a combinar; otra dificultad es la de identificar el tipo de operación que interviene en la resolución del problema. Si los alumnos tienen dificultades para formar el número, puede pedirles que digan dos números que podría tener la casa y, a partir de ahí, iniciar la elaboración de un diagrama de árbol. Pida a los alumnos que traten de completarlo o que encuentren las respuestas haciendo cálculos aritméticos. Posteriormente, usted puede plantear el mismo problema pero ahora sí se puede utilizar el cero en la segunda cifra. Pregunte: ¿cuántos números diferentes podrían ser? Incorpore este último problema al portafolios. Respuestas. a) 1, 2, 3, 4, 5, 6, 7, 8, 9. Nueve en total. b) 1, 3, 4, 5, 6, 7, 8, 9. Ocho en total. c) 72 pares de números. (Se multiplica 9 × 8).

Propósito del video: Conocer e identificar situaciones que se resuelven mediante procedimientos de conteo.