
|

|

|
 |
 |

| Propósito de la sesión. Resolver
problemas aditivos de fracciones con
distinto denominador.
Organización del grupo. Se sugiere que resuelvan en parejas las actividades, y que el apartado Lo que aprendimos se resuelva de manera individual. |

| Propósito del video. Presentar algunos ejemplos en los que es utilizada la suma y resta de fracciones. |

 |

| Sugerencia didáctica. Antes de que las parejas resuelvan, puede pedir que hagan un cálculo preguntándoles: "¿Creen que el grosor será más o menos de una pulgada? ¿Por qué?". En este momento no adelante respuestas, posteriormente verificarán su cálculo resolviendo el problema. Para que los alumnos tengan una mejor idea de la situación que se les plantea, puede sugerirles que utilicen una regla graduada en pulgadas y centímetros y así trabajar con los tamaños reales de las medidas de las tablas de madera (1 pulgada = 2.54 cm 1 cm = 0.395 pulgadas). |
| Eje |
| Sentido numérico y pensamiento algebraico. |
| Tema |
| Significado y uso de los números. |
| Antecedentes |
| Desde la escuela primaria los alumnos han utilizado los algoritmos para la suma y la resta de fracciones y de números decimales. En el primer grado de la escuela secundaria se espera que para sumar y restar números fraccionarios hagan uso de la equivalencia de fracciones, del cálculo mental y la estimación consolidando su uso mediante la resolución de diversos problemas. |
| Propósitos de la secuencia
Resolver problemas aditivos con números fraccionarios y decimales en distintos contextos. |
||
| Sesión | Título y propósitos de la sesión | Recursos |
| 1 | El festival de fin de cursos Resolver problemas aditivos de fracciones con distinto denominador. | Video "¿Dónde se utilizan las fracciones?" Interactivo |
| 2 | Marcas atléticas Comparar números decimales y fracciones con distinto denominador mediante la resta. | Video |
| 3 | Los precios de la cafetería Resolver problemas de suma y resta de números decimales. | |
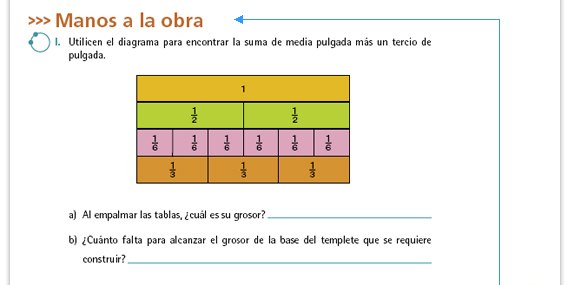
Respuestas. Es importante que los
alumnos se percaten de que en el
diagrama  equivale a equivale a  , y que , y que
 equivale a
equivale a  ; sumados dan ; sumados dan 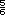 Por lo
tanto, las tablas de madera no son
suficientes para tener una pulgada de
grosor. Por lo
tanto, las tablas de madera no son
suficientes para tener una pulgada de
grosor.
En el mismo diagrama puede verse que si se tienen 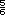 , para completar un
entero hace falta , para completar un
entero hace falta 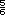 |

Sugerencia didáctica. Con objeto de
que los alumnos se familiaricen con la
equivalencia de fracciones, se sugiere
utilizar el diagrama. Las sumas podrían ser 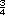 + +
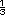 , ,  + +
 u otras. u otras. |

Respuestas. Es probable que los
resultados en todo el grupo no
sean los mismos, pero que sí sean
equivalentes. Una forma de calcular el
grosor es:
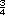 = = 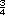
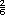 = = 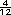
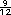 + + 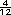 = =
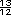
Otra forma consiste en multiplicar los denominadores entre sí para obtener un denominador común, y el numerador de una fracción por el denominador de la otra: 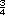 = = 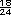
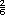 = = 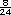
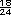 + + 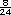 =
= 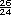 = = 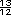
Por lo tanto, el grosor sería mayor que una pulgada. La parte sobrante sería 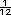 |

Respuestas. Una forma de calcular el
grosor es:
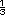 = = 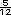
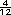 + + 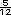 = =
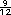 , por lo tanto, las tablas no son suficientes. , por lo tanto, las tablas no son suficientes.
La parte faltante es 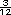 o o 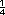 ( a
( a 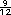 le faltan le faltan 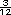 para ser 1). para ser 1).
|

Respuestas.  +
+ 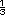 = = 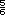 , falta , falta
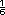 para tener una pulgada de espesor. para tener una pulgada de espesor.
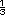 + + 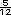 = =
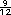 , le faltan
, le faltan 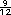 para tener
una pulgada de espesor. para tener
una pulgada de espesor.
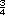 + + 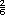 = =
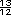 , le sobra
, le sobra 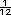 para tener
una pulgada de espesor.
La última es la que mas se acerca a la
medida deseada porque para tener
una pulgada de espesor.
La última es la que mas se acerca a la
medida deseada porque 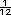 < < 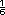 <
< 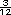 |

Respuestas. Hay distintas formas
de resolver cada una de las sumas:
sumar primero dos fracciones cuyos
denominadores sean múltiplos y
después sumar la tercera fracción; o
multiplicar desde el principio los tres
denominadores. Algunos ejemplos de
resolución son los siguientes:
|
Propósito del interactivo. Visualizar las operaciones de suma y resta de fracciones efectuadas a través de fracciones equivalentes. |

| Sugerencia didáctica. Pida a los alumnos que escriban y resuelvan en su cuaderno una suma de fracciones en la que el denominador común sea uno de los denominadores de las fracciones, y otra en la que deba obtenerse multiplicando los dos denominadores. |

| Propósito del interactivo. Visualizar las operaciones de suma y resta de fracciones efectuadas a través de fracciones equivalentes. |
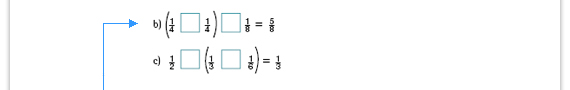
| Sugerencia didáctica. Es posible que
los alumnos no sepan qué significan
los paréntesis en las operaciones. En
secuencias posteriores lo trabajarán,
pero por lo pronto comente con ellos
que los paréntesis son una manera
de señalar que la operación que está
dentro debe resolverse primero.
Respuestas. Una forma de encontrar las respuestas es convirtiendo las fracciones de cada inciso en fracciones equivalentes con denominador común.
|

Sugerencia didáctica. Pida a los
alumnos que estimen la respuesta,
por ejemplo, en el caso del inciso a)
Será mayor o menor a 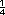 o a o a  ? En el
segundo caso pregunte si la respuesta
puede ser ? En el
segundo caso pregunte si la respuesta
puede ser 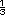 o si será mayor o menor
que o si será mayor o menor
que 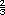
Integrar al portafolios. Estas operaciones ponen en juego los conocimientos de los alumnos sobre la suma de fracciones. Si les es difícil resolverlos convendría trabajar más sobre las equivalencias y la búsqueda del denominador común. Respuestas.
|
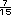 +
+ 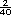 +
+
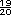 =
= 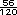 +
+ 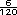 +
+ 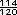 =
= 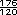 =
= 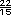
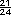 +
+  +
+
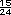 +
+ 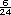 =
= 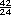 =
= 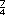
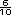 +
+ 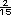 =
= 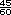 +
+ 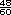 +
+ 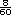 =
= 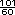
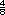 +
+  ) -
) -
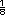 =
= 
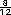 =
=