|

|

|
 |
 |

| Propósito de la sesión. Comparar
números decimales y fracciones con
distinto denominador mediante la
resta.
Organización del grupo. La sesión entera puede ser resuelta organizando a los alumnos en parejas. |

| Sugerencia didáctica. Los
alumnos pueden recurrir a distintos
procedimientos para la comparación
de fracciones, por ejemplo: ubicarlas
en la recta, obtener fracciones
equivalentes o compararlas mediante
productos cruzados.
Probablemente no todos los alumnos resuelvan correctamente el problema, en el siguiente apartado tendrán oportunidad de hacer las correcciones necesarias. |

Posibles procedimientos.
|

Respuestas. Se busca un
denominador comun
8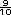 - 7 - 7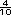 = 1
= 1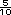 = 1 = 1 , o bien, se
escribe como fracción impropia , o bien, se
escribe como fracción impropia
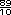 - - 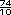 = =
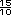 =
=  , o con números
decimales 8.9 . 7.4 = 1.5. Permita
que los alumnos decidan de que
manera encontrar la diferencia. Si
cometen errores podrán corregirlos
más adelante. , o con números
decimales 8.9 . 7.4 = 1.5. Permita
que los alumnos decidan de que
manera encontrar la diferencia. Si
cometen errores podrán corregirlos
más adelante.

Sugerencia didáctica. Si en el grupo hubo varias formas de calcular la diferencia, comenten si los resultados 1  , ,  , ,
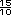 , 1.5 u otra equivalente son
números distintos o si son diferentes
maneras de expresar el mismo
número. Para algunos alumnos puede
ser difícil imaginar que un número
pueda expresarse de distintas formas
porque en su experiencia con los
números naturales un número solo
tiene una manera de expresarse. Para
comprenderlo podria serles útil hacer
representaciones gráficas como el
sombreado de areas o la ubicación en
la recta. , 1.5 u otra equivalente son
números distintos o si son diferentes
maneras de expresar el mismo
número. Para algunos alumnos puede
ser difícil imaginar que un número
pueda expresarse de distintas formas
porque en su experiencia con los
números naturales un número solo
tiene una manera de expresarse. Para
comprenderlo podria serles útil hacer
representaciones gráficas como el
sombreado de areas o la ubicación en
la recta. |
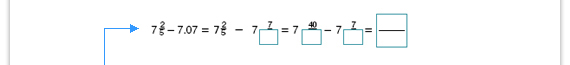
Respuestas. Hay que escribir 7.07
como 7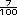 , entonces queda
7 , entonces queda
7 - 7 - 7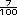 . Para hallar un
denominador comun el Libro
del alumno sugiere convertir los
quintos en centésimos . Para hallar un
denominador comun el Libro
del alumno sugiere convertir los
quintos en centésimos
7 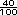 - 7 - 7 =
= 
|

Posibles procedimientos. Para
responder a estas preguntas los
alumnos necesitan hacer operaciones
entre números decimales y fracciones.
Podrían optar por escribir las
fracciones como números decimales o
viceversa.
|

Posibles procedimientos.
|
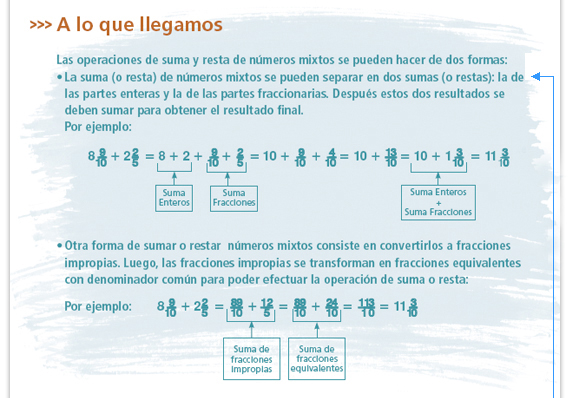
 Sugerencia didáctica. Pida a los
alumnos que copien esta información
en una cartulina o papel grande y que
la peguen en el salón.
Sugerencia didáctica. Pida a los
alumnos que copien esta información
en una cartulina o papel grande y que
la peguen en el salón. |

Respuestas y posibles
procedimientos.
|

Respuestas y posibles
procedimientos.
|
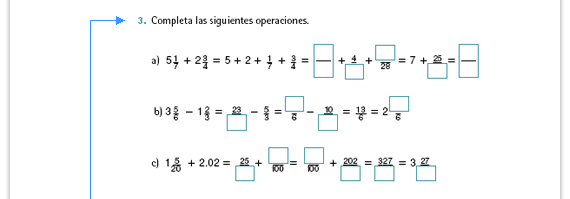
Respuestas.
|
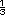 =
= 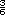 -
- 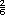 =
=
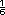
 -
- 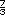 =
= 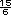 -
- 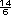 =
=
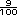 -
- 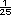 =
= 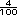 =
= 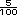 y se
simplifica a
y se
simplifica a 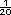
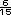 =
= 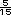 =
= 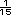
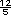 -
- 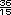 -
- 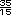 =
= 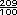 -
- 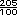 =
=
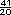 -
- 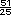 =
= 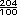 =
= 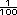
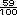 -
- 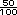 =
8
=
8 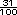
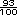 = 50.93
= 50.93
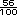 , se resta
, se resta
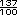 o 1
o 1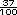
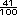 con decimales
con decimales
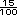
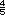
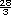
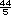 =
=
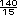
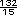 =
=
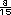 de metro por
segundo. Si se intenta hacer la
resta entre los enteros por un lado
y las fracciones por otro, puede
haber confusion. De la resta de
enteros el resultado es 1, pero al
restar las fracciones se obtendría
de metro por
segundo. Si se intenta hacer la
resta entre los enteros por un lado
y las fracciones por otro, puede
haber confusion. De la resta de
enteros el resultado es 1, pero al
restar las fracciones se obtendría
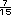 Esos
Esos 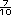 =
= 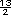 +
+ 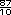 =
=
 +
+ 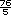 y se pasa a número mixto:
15
y se pasa a número mixto:
15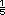
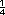 - 15
- 15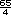 -
- 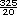 -
- 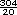 =
= 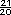 = 1
= 1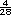 +
+ 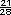 = 7 +
= 7 + 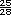 = 7
= 7 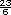 -
- 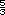 =
= 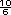 =
= 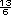 = 2
= 2 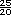 +
+ 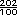 =
= 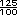 +
+ 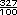 = 3
= 3