
|

|

|
EXAMEN BLOQUE 1 |
Matemáticas I |
 |
|
PROPUESTA DE EXAMEN BIMESTRAL BLOQUE 1 |
|
SECUENCIA 8. PROBLEMAS DE CONTEO
Reactivo 1
-
1. Se quieren elaborar banderas de dos franjas y colores diferentes, para lo cual se tiene tela de los siguientes tres colores: blanco, rojo y verde.
| Inciso a)" |
¿Cuáles de los siguientes procedimientos corresponden al total de banderas diferentes que se pueden elaborar?
-
a) 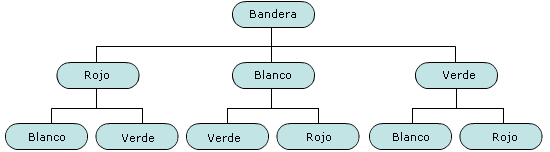
-
b) 3 × 3 -
c) 
-
d) blanco, rojo
blanco, verde
blanco, blanco
verde, rojo
verde, blanco
verde, verde
rojo, blanco
rojo, verde
rojo, rojo
-
1'. Relaciona las columnas anotando en cada paréntesis la letra del inciso que le corresponda. Puede repetirse más de una letra.
| ( ) ¿De cuántas formas se puede armar un juego de alhajas si se tienen tres tipos de aretes, dos de pulseras y cuatro de anillos? (El juego de alhajas se forma con un tipo de aretes, pulsera y anillo) | A. 4 × 3 |
| ( ) ¿Cuántos viajes directos diferentes se pueden realizar si hay cuatro ciudades de salida y tres ciudades de llegada? (Un viaje directo es ciudad de salida-ciudad de llegada) | 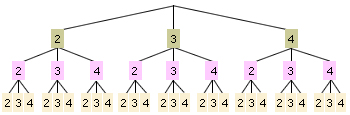 |
| ( ) ¿Cuántos números diferentes de tres cifras se pueden formar con los dígitos 4, 3 y 2? (Los números se pueden repetir) | |
| ( ) ¿De cuántas formas se pueden combinar tres blusas y cuatro faldas? (Utilizando únicamente una blusa y una falda) | C. 2 × 3 × 4 |
Reactivo 2
-
1. ¿Cuántas banderas de tres franjas pueden hacerse si se tiene tela de cuatro colores diferentes (azul, blanco, rojo y verde) y se puede repetir un mismo color en franjas separadas?
-
a) 4 × 3 × 1 -
b) 4 × 3 × 2 -
c) 4 × 3 × 3 -
d) 4 × 3 × 4
| Inciso c) |
-
1'. En un restaurante una persona puede elegir entre dos sopas, cuatro guisados y tres postres. ¿De cuántas formas diferentes puede elegir su menú?
-
a) 9 -
b) 12 -
c) 18 -
d) 24
| Inciso d) Se puede obtener: 2 × 4 × 3 = 24 |
Reactivo 3
-
1. ¿De cuántas formas diferentes se puede ir de la ciudad A a la ciudad D, pasando por las ciudades B y C? (sin que haya retrocesos).

| Comentario: los alumnos pueden enumerar los caminos y hacer un diagrama de árbol, lista, arreglo o aplicar la regla del producto 3 × 2 × 4, y obtener las 24 formas diferentes en que se puede ir de A a D |
-
1'. En un restaurante, una persona puede escoger entre dos sopas, cuatro guisados y tres postres. Se ha pensado ofrecer más combinaciones de menú agregando un platillo. Para que el número de combinaciones sea el mayor posible, ¿qué conviene aumentar? (un menú se forma con una sopa, un guisado y un postre).
-
a) El número de sopas -
b) El número de guisados -
c) El número de postres -
d) Cualquiera de los tres
| Inciso a) Comentario: la operación sería 3 × 4 × 3 y se obtendrían 36 combinaciones diferentes. |