Propósito de la sesión. Interpretar la ecuación como una expresión que sintetiza las relaciones entre los datos y la cantidad desconocida del problema. Resolver problemas que implican plantear y resolver ecuaciones algebraicas aditivas del tipo x + a = b. Organización del grupo. Se sugiere que trabajen todas las actividades organizados en parejas.

Eje

Sentido numérico y pensamiento algebraico.

Tema

Significado y uso de las operaciones.

Antecedentes

En las secuencias 3 y 4 los alumnos se iniciaron con la utilización de literales para expresar patrones y fórmulas geométricas. En esta secuencia usarán literales para traducir el texto de un problema al código algebraico y para resolver ecuaciones.

Propósitos de la secuencia Resolver problemas que impliquen el planteamiento y la resolución de ecuaciones de primer grado de las formas x + a = b; ax = b; ax + b = c, utilizando las propiedades de la igualdad, cuando a, b y c son números naturales y decimales.
Sesión	Título y propósitos de la sesión	Recursos
1	A repartir naranjas Interpretar la ecuación como una expresión que sintetiza las relaciones entre los datos y la cantidad desconocida del problema. Resolver problemas que implican plantear y resolver ecuaciones algebraicas aditivas del tipo x + a = b.	Interactivo "Ecuaciones" Aula de Medios "A repartir naranjas" (Hoja de cálculo)
2	El paseo escolar Resolver problemas que implican plantear y resolver ecuaciones algebraicas del tipo ax = b.	Video "El terreno y el río" Interactivo "Ecuaciones"
3	Resolución de ecuaciones mixtas Resolver problemas que implican plantear y resolver ecuaciones algebraicas del tipo ax + b = c.	Interactivo "Ecuaciones de primer grado"

Propósitos de la actividad. Se trata de un problema sencillo que se resuelve con la suma 24 + 8. Se espera que los alumnos identifiquen cuáles son los datos conocidos y cuál es la operación que resuelve el problema. Es importante que identifiquen como una igualdad la expresión en la que aparece el signo igual. En este momento no es necesario que definan el concepto de igualdad, sino sólo que empiecen a reconocer y a utilizar el término. Posibles dificultades. Dado que aparecen las palabras "tenía", "vendió", algunos alumnos podrían pensar que el problema se resuelve con la resta 24 - 8. Si bien está implícita una resta, el problema se resuelve mediante una suma (cantidad final de naranjas más cantidad de naranjas vendidas).

Sugerencia didáctica. En caso de que algunos alumnos presenten una respuesta distinta a 32 kilogramos, pídales que comenten cómo lo obtuvieron. Posteriormente invite al grupo a que resuelvan la actividad I del apartado Manos a la obra para verificar si la respuesta que dieron es correcta o no.

Propósito del interactivo. Resolver ecuaciones de primer grado utilizando las propiedades de la igualdad.

Propósito de la actividad. Que los alumnos continúen identificando los datos conocidos y los desconocidos de un problema, y que resuelvan problemas de suma o resta mediante la operación inversa. Recuerde que. Los problemas aditivos son aquellos que implican tanto a la suma como a la resta. Cuando en una suma se desconoce uno de los datos, se puede encontrar el dato faltante mediante una resta, que es la operación inversa de la suma. En este caso, el dato desconocido de la suma se encuentra mediante una resta: 124 - 57 = 67. Los alumnos irán identificando estas relaciones en el transcurso de las actividades de este apartado y podrán formalizarlo al final de esta sesión.

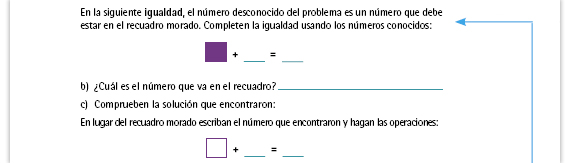
Propósito de la actividad. Que los alumnos analicen la estructura del problema (los datos y la forma en que están relacionados) para identificar cómo está conformada una igualdad. Aproveche diferentes momentos para que los alumnos se vayan familiarizando con el término "igualdad"; insista en que una igualdad comprende las expresiones que están de uno y del otro lado del signo igual.

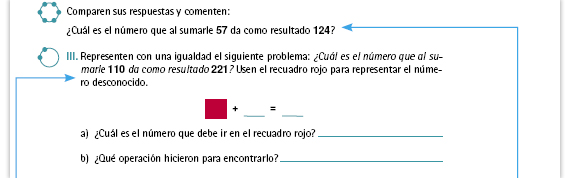
Propósito de la actividad. Que los alumnos logren expresar mediante una igualdad, un problema que se les presenta de manera verbal. Esto implica identificar cuáles son los datos conocidos y desconocidos, y cómo se relacionan entre ellos: + 110 = 221 Posibles procedimientos. Puede hacerse restando 221 - 110 o pensando cuánto le falta a 110 para llegar a 221.

Sugerencia didáctica. Es importante que se comente cómo se obtiene el resultado. Algunos restarán 124 - 57, otros lo harán pensando cuánto le hace falta a 57 para llegar a 124; ambas formas de resolver implican a la resta.

Propósito de la actividad. En secuencias anteriores los alumnos han utilizado letras para expresar fórmulas y patrones numéricos; en esta secuencia se pretende que los alumnos utilicen una letra (en este caso la x) para representar al dato desconocido (incógnita) en una igualdad. Es importante que los alumnos identifiquen a la x no como una letra, sino como un número del que se desconoce su valor.

Sugerencia didáctica. Si los alumnos tienen dificultades para completar la ecuación, se les puede pedir que completen lo siguiente: x = 221 - _____ x = ______

Sugerencia didáctica. Si los alumnos muestran facilidad para realizar estos ejercicios, puede proponerles que verifiquen el valor de x sustituyéndolo en la ecuación: x + 110 = 221 111 + 110 = 221 221 = 221

Sugerencia didáctica. Lea y comente esta información con sus alumnos. Destaque las siguientes ideas: -Las igualdades que aparecieron en las actividades anteriores tenían sólo números, ahora se presentan igualdades en las que se utilizan letras para representar un dato desconocido (incógnita). -Estas igualdades se llaman "ecuaciones". Puede pedirles que en su cuaderno respondan a la pregunta "¿Qué es una ecuación?". Pida a algunos alumnos que lean sus respuestas y, a partir de ellas, usted puede ampliarlas incorporando otros términos que las enriquezcan. Por ejemplo: "Es una igualdad en la que hay una incógnita que se representa con una letra", "Es una expresión algebraica en la que hay una incógnita". Una vez que se hayan leído y comentado algunas respuestas, los alumnos pueden hacer correcciones o ampliar lo que inicialmente habían escrito.

Propósito del interactivo. Resolver ecuaciones de primer grado utilizando las propiedades de la igualdad.

Sugerencia didáctica. Aclare a los alumnos que, en general, puede utilizarse cualquier letra para representar un valor desconocido o incógnita (no siempre es la letra x ). Para el inciso c), comente que una característica fundamental de toda igualdad es que lo que aparece del lado izquierdo del signo igual, debe tener el mismo valor que lo que está en el lado derecho, por lo que es importante verificar que el valor que se le ha asignado a las incógnitas es correcto.

Sugerencia didáctica. Una forma más de ejemplificar esta información, es "Lo contrario de sumar, es restar: si a un número le sumo 5 y al resultado le resto 5, obtenemos el mismo número". Puede preguntar a los alumnos lo siguiente: -Si en una adición se desconoce un sumando ¿qué operación se realiza para calcularlo? -Si en una sustracción se desconoce el minuendo ¿qué operación se realiza para calcularlo?

Propósito de la actividad. A la cantidad inicial, que es la incógnita del problema, se le aplican dos operaciones sucesivas y se obtiene un resultado determinado. A partir de esas transformaciones y del resultado, que son los datos conocidos, debe obtenerse el valor de la incógnita. Respuesta. Las dos últimas ecuaciones representan el problema.

Sugerencia didáctica. Pida que pasen algunos alumnos al pizarrón a resolver cada una de las ecuaciones elegidas y que identifiquen cuáles ecuaciones plantean el problema de manera adecuada. Es importante destacar que en el caso de la primera expresión algebraica no se plantea ninguna igualdad, a diferencia de las otras tres.

Sugerencia didáctica. Subraye el hecho de que con las dos últimas ecuaciones se obtiene la misma solución porque plantean el mismo problema: restar primero 11 kg y después 13 kg, es lo mismo que restar 24 kg en una sola operación.

Posibles procedimientos. Pueden resolver el problema de distintas maneras. Una de ellas es partir de los 15 litros con los que se quedó, e ir agregando los litros que fue entregando en cada tienda: 15 + 34 + 56 = 105 litros. Y después se restan los 21 litros que había recogido en otro pueblo: 105 - 21 = 84 litros. Otra forma es sumar las cantidades de litros entregados (56 + 34 = 90), restarles los 21 litros que se agregaron en otro pueblo (esos litros no salieron del primer establo): 90 - 21 = 69, y sumar después los 15 litros que sobraron: 69 + 15 = 84 Sugerencia didáctica. Ayúdeles a comprender cómo fueron variando las cantidades haciéndoles preguntas como: ¿Sabemos con cuántos litros de leche salió el camión del primer pueblo? ¿Qué pasó después, entregó o recibió más litros de leche? ¿A qué se refiere el número 21? ¿A qué se refiere el número 56? Posteriormente puede pedir a los alumnos que comenten por qué las ecuaciones x + 21 - 56 - 34 = 15, y x - 69 = 15, tienen la misma solución.

Integrar al portafolios Si identifica que los alumnos tienen dificultades para plantear las ecuaciones, repase con el grupo las actividades III y IV del Manos a la obra y el segundo A lo que llegamos, con la finalidad de enfatizar cuáles son las operaciones que permiten encontrar el número buscado una vez que se ha planteado la ecuación. Respuestas. a x + 27 = 139 x = 138 - 27 x = 111 b x - 2.73 = 5.04 x = 5.04 + 2.73 x= 7.77