
|

|

|
 |
 |

| Propósito de la sesión. Resolver
problemas que implican plantear y
resolver ecuaciones algebraicas del
tipo ax = b.
Organización del grupo. Forme parejas para que trabajen de esa manera durante toda la sesión. |

| Propósito de la actividad. El problema que ahora se plantea es de tipo multiplicativo: implica a la división y a la multiplicación. Encontrar el resultado es relativamente sencillo, pues los alumnos pueden identificar rápidamente que el problema se resuelve con una división, y los números que se dividen son enteros y con pocas cifras. La parte central de la actividad es que los alumnos traten de plantear -y resolver- una ecuación que represente el problema; no importa si en este momento no logran hacerlo de manera correcta, lo importante es que exploren distintas posibilidades. |

| Sugerencia didáctica. Es posible que la mayoría de los alumnos haya logrado encontrar el resultado del problema mediante la división 280 ÷ 8, pero que no todos hayan logrado plantear la ecuación. Pida a estos alumnos que expliquen cómo resolvieron el problema, aunque no hayan podido plantear la ecuación; después pida a quienes sí lo hayan podido hacer, que muestren al grupo sus respuestas. Pregunte al grupo: ¿Cómo podemos saber cuál es la respuesta correcta? |

| Respuesta. 8y = 280. Esta ecuación representa que en cada camión hay "y" niños; como hay 8 camiones, con 8y se obtiene la cantidad total de niños, que es de 280. |

| Respuesta. Para encontrar el valor de y se divide 280 ÷ 8. |

| Propósito del interactivo. Resolver ecuaciones de primer grado utilizando las propiedades de la igualdad. |

| Sugerencia didáctica. En caso de que algunas parejas hayan
elegido ecuaciones que no corresponden con el problema, pida
que hagan la comprobación en el pizarrón. Los alumnos pueden
comentar por qué esa ecuación no permite obtener el resultado
correcto. Asimismo, es importante que se contraste con la
ecuación correcta y que se muestre su comprobación. Destaque
el hecho de que la ecuación plantea una multiplicación, y la
operación con la que se resuelve es una división:
8y = 280 y = 280 ÷ 8 y = 35 |

| Respuesta. Las ecuaciones que corresponden al problema son la segunda y la tercera. |
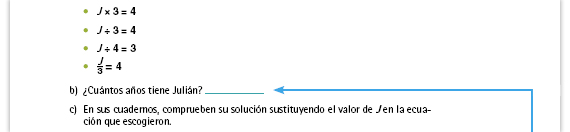
| Posibles procedimientos. Algunos alumnos quizá resuelvan el problema sin plantear la ecuación, aun cuando la hayan identificado. Pueden sumar 3 veces 4, o multiplicar 3 x 4, que es una forma correcta de resolver, pues para encontrar el valor de J es necesario realizar la multiplicación 3 x 4. Trate de identificar qué alumnos sí recurren a la ecuación y quiénes no. |

Sugerencia didáctica. Pida a dos
alumnos que resuelvan en el pizarrón
las ecuaciones que corresponden
al problema, y que sustituyan la
incógnita para hacer la comprobación.
Pregunte a los alumnos por qué las
expresiones J ÷ 3 = 4
y 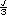 = 4 dan
el mismo resultado. Aclare que si bien
ambas ecuaciones expresan
una división, en el lenguaje algebraico
se utiliza más la raya ( = 4 dan
el mismo resultado. Aclare que si bien
ambas ecuaciones expresan
una división, en el lenguaje algebraico
se utiliza más la raya ( 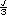 = 4) para
indicar una división y se usa poco el
signo de la división. = 4) para
indicar una división y se usa poco el
signo de la división. |

| Propósito de la actividad. Se
espera que los alumnos establezcan
relaciones entre los distintos
momentos por los que han transitado
en estas dos sesiones para encontrar
el valor de una incógnita: el
planteamiento verbal del problema, su
expresión algebraica y la resolución
aritmética.
Sugerencia didáctica. Mientras las parejas resuelven, reproduzca la tabla en el pizarrón para que puedan comparar sus respuestas. Pida a algunos alumnos que pasen a completar la tabla. Es posible que aparezcan distintas formas correctas de expresar las ecuaciones, si no es así, es conveniente que usted las proponga, por ejemplo: En el segundo renglón, x ÷ 6 = 48 es lo mismo que 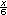 = 48 = 48
En el tercer renglón, m x 25 = 165 es lo mismo que 25m = 165 (de hecho, esta última expresión es más adecuada que la anterior, pues el signo de multiplicación podría confundirse con la literal x). En el cuarto renglón, la ecuación puede ser: y ÷ 7 = 12.5 o  = 12.5 = 12.5 |

 Lea y comente esta información con
los alumnos. Puede pedirles que
busquen en esta misma sesión otros
ejemplos en los que la ecuación
se resuelva mediante una división
o una multiplicación. La idea de
que la multiplicación y la división
son operaciones inversas puede
ejemplificarse de la siguiente manera:
"Lo contrario de multiplicar es dividir:
si un número lo multiplicamos por 6
y el resultado lo dividimos entre 6,
obtenemos el mismo número". Y
viceversa.
Lea y comente esta información con
los alumnos. Puede pedirles que
busquen en esta misma sesión otros
ejemplos en los que la ecuación
se resuelva mediante una división
o una multiplicación. La idea de
que la multiplicación y la división
son operaciones inversas puede
ejemplificarse de la siguiente manera:
"Lo contrario de multiplicar es dividir:
si un número lo multiplicamos por 6
y el resultado lo dividimos entre 6,
obtenemos el mismo número". Y
viceversa. |

| Propósitos del video. Observar el planteamiento y la solución de problemas con un valor desconocido. |
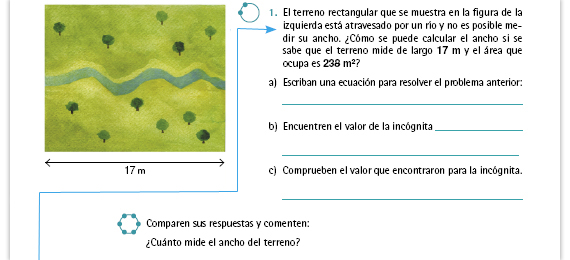
| Propósito de la actividad. Se
conoce la medida del largo y la
superficie total, la incógnita es la
medida del ancho. Pueden resolver el
problema dividiendo la superficie
entre la medida del largo sin recurrir
a una ecuación. Lo relevante es que
logren plantear la ecuación y que
encuentren el valor de la incógnita
resolviendo la ecuación.
Sugerencia didáctica. Pida a uno o dos de los alumnos que resuelvan en el pizarrón la ecuación que plantearon y que hagan la comprobación. Respuesta. 17y = 238 y = 238 ÷ 17 (o también y = 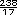 ) )
y = 14 |