
|

|

|
 |
 |

| Propósito de la sesión. Resolver
problemas que implican plantear y
resolver ecuaciones algebraicas del
tipo ax + b = c.
Organización del grupo. Se sugiere resolver todas las actividades en parejas, a excepción del apartado Lo que aprendimos, que puede resolverse de manera individual. |

| Propósito de la actividad. Este
problema implica dos
transformaciones sucesivas de la
cantidad inicial: primero se multiplica
y luego se resta.
Posibles dificultades. Si algunos alumnos siguen utilizando el signo de la multiplicación, usted puede sugerirles que lo cambien por la expresión 3x para evitar confusiones. Podrían tener mayores dificultades para resolver la ecuación en la que se se aplican dos operaciones a la cantidad inicial: una multiplicación y una suma. ¿Qué se resuelve primero? Permita que los alumnos exploren la manera de encontrar el valor de la incógnita cuando la ecuación implica una operación aditiva. |

| Sugerencia didáctica. Mientras los alumnos resuelven, identifique dos o tres procedimientos que puedan apoyar a los demás alumnos en el planteamiento de la ecuación y en su resolución. Pida a esos alumnos que muestren su solución a todo el grupo. En las actividades del siguiente apartado tendrán oportunidad de encontrar una forma correcta de plantear y resolver la ecuación. |

| Propósito de las actividades. Los
alumnos podrán identificar los datos
conocidos y la incógnita, así como las
relaciones que se establecen entre
ellos; esto les permitirá identificar
la ecuación que corresponde al
planteamiento del problema.
Respuesta. La incógnita es el número que pensó Juan, y la ecuación correcta es 3x - 5 = 10. |

| Sugerencia didáctica. Pida a los alumnos que argumenten por qué esa ecuación no corresponde con el problema. Deben darse cuenta de que en esta ecuación los números no corresponden con las operaciones realizadas. Puede pedir que sustituyan x por el valor encontrado anteriormente, para ver si obtienen el mismo resultado que con la ecuación correcta. |

| Propósito de la actividad. Para encontrar el valor de la incógnita deben considerar que la operación inversa de la resta es la suma; por lo tanto, para saber cuál fue el número que obtuvo Juan al hacer la operación 3x, es necesario sumar 5 al resultado final: 10 + 5 = 15. |

| Propósito de la actividad. La operación inversa de la multiplicación es la división, por lo tanto, tendrían que dividir 15 ÷ 3 para encontrar el valor de x. |

| Sugerencia didáctica. Puede pedir a un alumno que haga la comprobación en el pizarrón. Pida a los alumnos que regresen a la solución que dieron al mismo problema al inicio de la sesión, para que comparen la ecuación y la solución que dieron en ese momento con lo que obtuvieron ahora. Pídales que hagan las correcciones necesarias. |

| Propósito de la actividad. Al
igual que en la actividad anterior,
se pretende que los alumnos
identifiquen que en la ecuación hay
dos operaciones, una multiplicativa
(en este caso la división y ÷ 4) y otra
aditiva (en este caso, la suma + 56), y
que primero se resuelve la operación
aditiva mediante la operación inversa:
al resultado final se debe restar 6, que
es lo que se había agregado.
Respuesta. Pueden utilizar y ÷ 4 + 6 = 11 o tambien 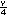 + 6 = 11. + 6 = 11. |

| Sugerencia didáctica. Asegúrese de que los alumnos efectivamente hagan la comprobación en sus cuadernos; para ello, deben sustituir la incógnita por el valor que encontraron: 20 ÷ 4 + 6 = 5 + 6 = 11. |

 Anime a los alumnos para que
argumenten por qué esa ecuación
no resuelve el problema (una posible
respuesta es que las operaciones
ni lo números coinciden con los
del problema planteado). Si los
argumentos no son suficientes, pueden
sustituir la incógnita por el valor que
ya encontraron, y ver si obtienen el
mismo resultado.
Anime a los alumnos para que
argumenten por qué esa ecuación
no resuelve el problema (una posible
respuesta es que las operaciones
ni lo números coinciden con los
del problema planteado). Si los
argumentos no son suficientes, pueden
sustituir la incógnita por el valor que
ya encontraron, y ver si obtienen el
mismo resultado. |

| Propósito de la actividad. La
incógnita de la ecuación que
corresponde a este problema está
determinada por dos operaciones.
Se espera que, a partir de lo que
trabajaron en la actividad anterior,
los alumnos puedan identificar la
ecuación que corresponde al
problema y resolverla.
Respuesta. La segunda ecuación (2a + 1 = 7.2) y la cuarta (a × 2 + 1 = 7.2) permiten encontrar el valor de la altura. |

| Respuesta. La segunda y la cuarta ecuación son las correctas. Conviene que aclare a los alumnos que la respuesta óptima es la segunda ecuación, pues en la cuarta se está utilizando el signo × para indicar la multiplicación, lo cual podría resultar confuso. En caso de que haya alumnos que hayan elegido otras ecuaciones, puede pedirles que las resuelvan y que después hagan la comprobación, para que de esa manera se percaten del error. |

| Propósito de la actividad. Se espera
que los alumnos apliquen lo aprendido
en las sesiones anteriores para resolver
estos problemas. Una particularidad de los
problemas que aquí se plantean, es que se
hace uso de números decimales.
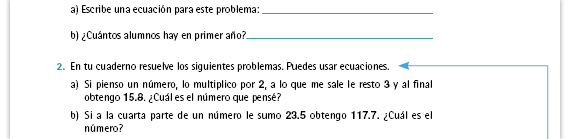
Sugerencia didáctica. Para cada uno de los siguientes problemas solicite a los alumnos que hagan las comprobaciones en sus cuadernos. Recuérdeles también que pueden usar las literales que quieran. Respuestas. 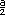 + 29 = 44. También
(a ÷ 2) + 29 = 44. El número de alumnos
es 30 (puede usar cualquier literal). + 29 = 44. También
(a ÷ 2) + 29 = 44. El número de alumnos
es 30 (puede usar cualquier literal). |
Respuestas.
|

| Propósito del interactivo. Resolver ecuaciones mixtas de primer grado respetando el orden de las operaciones. | Respuestas.
|

| Integrar al portafolios. Si identifica
dificultades para plantear la ecuación,
pida a uno o dos alumnos que lo hayan
hecho correctamente que la escriba en el
pizarrón. Usted puede preguntar: ¿Cuál
es la incógnita? ¿Cómo fue cambiando el
dinero que inicialmente tenía Eugenio?
¿Con cuánto dinero se quedó al final?
¿Cómo podemos plantear la igualdad?
Si los alumnos tienen dificultades para
resolver la ecuación repase con ellos el
apartado A lo que llegamos de las sesiones
2 y 3 de esta secuencia.
Respuestas. 3x - 150 = 300 (3x - 150) ÷ 3 = 100 Con el propósito de apoyar a aquellos alumnos que aún no hayan comprendido el problema, y para revisar una forma más de resolverlo sin plantear la ecuación, usted puede comentar el siguiente procedimiento: Si repartió $100 a cada amigo quiere decir que a Eugenio le quedaban $300. Si gastó $150, entonces tenía $450 (considerando los $300); esa fue la cantidad que retiró. Si esa cantidad se obtuvo al triplicarse su dinero, entonces inicialmente había depositado $150. |
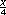 + 23.5 = 117.7
+ 23.5 = 117.7