Propósito de la sesión. Identificar que no siempre es posible construir un triángulo dadas tres medidas. Conocer la propiedad que deben cumplir tres medidas para que sea posible trazar un triángulo. Materiales. Popotes o tiras de cartoncillo, tijeras, regla y compás. Organización del grupo. Se sugiere que el problema inicial se resuelva en equipos, y la sección Manos a la obra, en parejas.

Eje

Forma, espacio y medida.

Tema

Figuras geométricas.

Antecedentes

A diferencia de las construcciones geométricas que se realizan en la escuela primaria, en este grado se espera que con base en procedimientos específicos los alumnos logren anticipar, probar y justificar los datos que son necesarios y suficientes para llevar a cabo una construcción. Para ello se apoyarán en procedimientos que ya conocen: -Trazos con regla y compás de triángulos y cuadriláteros. -Trazo de ángulos dada su medida.

Propósitos de la secuencia Construir triángulos y cuadriláteros. Analizar las condiciones de existencia y unicidad
Sesión	Título y propósitos de la sesión	Recursos
1	¿Existe o no existe? Identificar que no siempre es posible construir un triángulo dadas tres medidas. Conocer la propiedad que deben cumplir tres medidas para que sea posible trazar un triángulo.	Interactivo "Desigualdad triangular"
2	¿Es uno o son muchos? Analizar y explorar casos sencillos de existencia y unicidad en la construcción de cuadriláteros.	Video "¿Es uno o son muchos?" Aula de medios "Es uno o son muchos" (Geometría dinámica)

Propósito de la actividad. Que los alumnos desarrollen su capacidad para cuestionarse acerca de dos hechos: 1.. ¿Tiene solución este problema? Es decir, ¿existe la solución? 2.. Si existe la solución, ¿es única o son varias las soluciones correctas? Se espera que los alumnos se den cuenta de que, dadas tres medidas, no siempre es posible construir un triángulo cuyos lados tengan, precisamente, esas medidas. Es decir, se trabaja en torno de la existencia o no existencia de la solución de un problema. Posibles procedimiento. Tal vez algunos alumnos no necesiten manipular los popotes para completar la tabla; si es así, pídales que los usen después para comprobar sus hipótesis; esto permitirá que los integrantes del equipo validen los resultados obtenidos.

Respuesta. Sólo es posible formar un triángulo con las medidas 8, 6 y 4 cm, y con las medidas 6, 4 y 3 cm.

Respuestas. a) No. b) La medida que los alumnos propongan para cada uno de los lados debe ser menor que la suma de los otros dos lados. Podrán anotar cualquiera de las siguientes opciones: (8, 6, 5); (8, 6, 4); (8, 6, 3); (8, 5, 4); (6, 5, 4); (6, 5, 3); (6, 5, 2); (6, 4, 3); (5, 4, 3); (5, 4, 2); (4, 3, 2). c) Debe haber un lado que sea mayor o igual que la suma de los otros dos. El alumno podrá contestar cualquiera de las siguientes opciones: (8, 6, 2); (8, 5, 3); (8, 5, 2); (8, 4, 3); (8, 4, 2); (8, 3, 2); (6, 4, 2); (6, 3, 2); (5, 3, 2). Sugerencia didáctica. Recomiende a los alumnos que para verificar rápidamente si las medidas propuestas permiten formar un triángulo, sumen las medidas de los lados menores. Esa suma debe ser mayor que la longitud del lado más grande. Cuando se comparen las respuestas de los incisos b) y c) invite a los alumnos a que las verifiquen usando los popotes. Pregunte también cómo podrían saber si se puede o no formar el triángulo, pero sin usar los popotes. Esto tiene el propósito de que analicen las ternas de números y traten de encontrar la relación entre ellos para determinar la existencia o no existencia del triángulo.

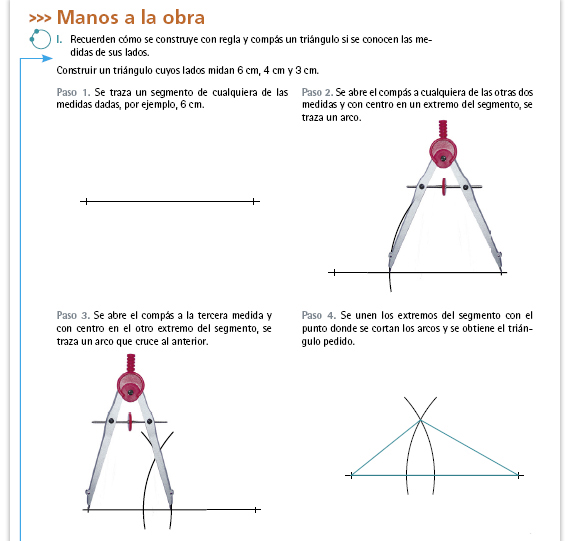
Sugerencia didáctica. Aunque los alumnos estudiaron el trazo de triángulos en la primaria es probable que ya no lo recuerden, por ello cerciórese de que las parejas sigan de manera correcta los pasos enunciados. Permita que sean ellos quienes interpreten las instrucciones; si nota que tienen dificultades, trate de auxiliarlos.

Propósito de la actividad. Con los incisos c), d) y e) se promueve que los alumnos identifiquen que dadas dos magnitudes para los lados de un triángulo, éste no queda completamente definido, lo que da lugar a varias respuestas. Respuestas. a) y b) El triángulo con las medidas 6, 3 y 2 cm es imposible de trazar. c) El tercer lado puede medir 8, 7, 6, 5 o 4 cm, aunque también puede tener una medida no entera, como 6.5, 7.5 cm; es probable que los alumnos no consideren estas soluciones, pero si alguno lo hace será interesante comentarla en el grupo. d) Si la tercera medida es un número entero, entonces hay cinco soluciones: 8, 7, 6, 5 y 4. e) El triángulo que los alumnos tracen deberá cumplir con la condición de las medidas que se dan. El tercer lado deberá medir más de 3 cm y menos de 9 cm.

Propósito del interactivo. Explorar cómo deben ser las medidas de los lados de un triángulo para poder trazarlo.

Sugerencia didáctica. Mientras las parejas resuelven, observe qué medidas son las que propusieron, de tal manera que usted pueda identificar si los alumnos han elaborado ya alguna hipótesis respecto de las condiciones para que sea posible el trazo de un triángulo. Asegúrese de que los alumnos efectivamente construyan el triángulo en sus cuadernos para que puedan verificar sus respuestas.

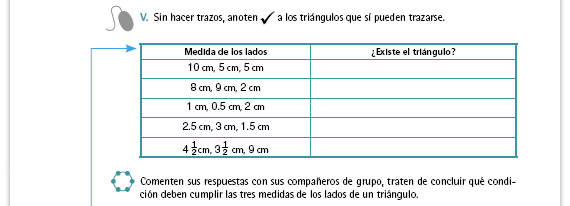
Sugerencia didáctica. Es importante que para completar esta tabla ya no hagan uso de material concreto ni de los trazos, sino que atiendan a las relaciones entre los lados con el fin de que pongan en juego las conjeturas que fueron construyendo a lo largo de las actividades anteriores. En la puesta en común tendrán oportunidad de validar sus respuestas. Respuestas. Sólo es posible trazar un triángulo con las siguientes medidas: 8, 9 y 2 cm, y 2.5, 3 y 1.5 cm. En el caso del primer renglón de la tabla, es la primera vez que se presenta un caso en el que la suma de dos lados es igual a la del lado mayor. Pida a los alumnos que comenten por qué no es posible trazar este triángulo.

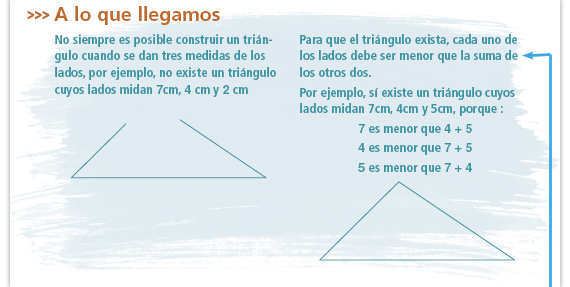
Además de leer la información, pueden reproducirla con sus propias palabras de manera verbal o por escrito en sus cuadernos; también pueden dar ejemplos diferentes a los mostrados o localizar en el mismo libro alguna actividad que la identifique. Integrar al portafolios. Solicite a los alumnos que realicen el siguiente ejercicio: a) Proponer unas medidas, distintas a las que se han dado anteriormente, con las cuales sea imposible construir un triángulo. Escribir por qué no es posible construirlo. b) Proponer unas medidas (distintas a las de los ejercicios anteriores) con las cuales sí sea posible construir un triángulo. Trazar el triángulo. Si los alumnos muestran dificultades para establecer cuáles son las condiciones para que esta figura exista, revise nuevamente con ellos la información del apartado A lo que llegamos.