Propósito de la sesión. Analizar y explorar casos sencillos de existencia y unicidad en la construcción de cuadriláteros. Organización del grupo. Se sugiere trabajar en equipos durante toda la sesión, incluyendo momentos de intercambio con todo el grupo. Materiales. -Popotes o tiras de cartoncillo cortados en las medidas que se indican. -Tachuelas o hilo y aguja. -Regla, compás, escuadras y transportador.

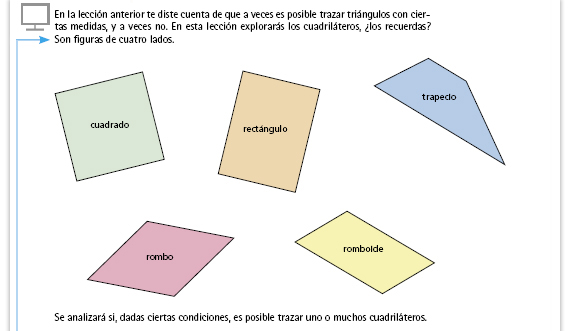
Sugerencia didáctica. De manera breve, haga un recordatorio sobre lo que es un cuadrilátero, solicitando a los alumnos que mencionen las características principales de los cuadriláteros que aquí se muestran y de otros que conozcan.

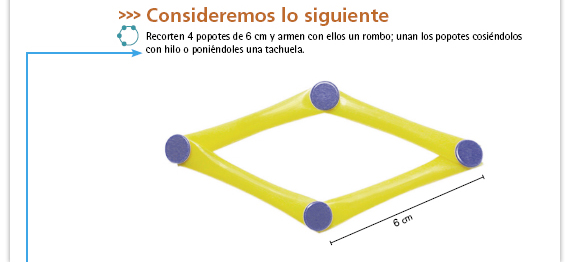
Sugerencia didáctica. La manipulación con material concreto es de gran ayuda para ciertos aprendizajes matemáticos. En este caso, el uso del material que se sugiere ayudará a que los alumnos se den cuenta de que existen rombos que son diferentes aunque sus lados midan lo mismo. Notarán que la medida de los popotes no varía, pero la medida de los ángulos que forman sí. Asegúrese de que se cuente con este material de manera oportuna y que los alumnos efectivamente lo empleen para realizar las actividades que se indican.

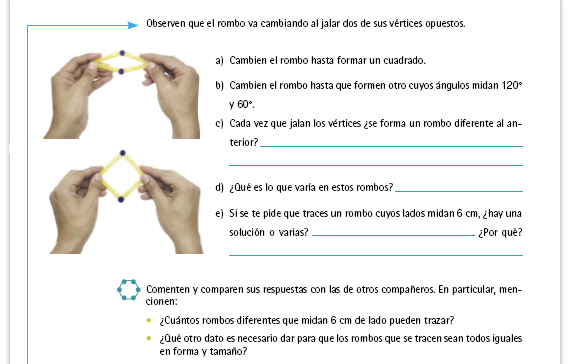
Sugerencia didáctica. Para el inciso a) es necesario que los alumnos se cercioren de que, efectivamente, su figura es un cuadrado; para ello pueden usar el ángulo recto de una hoja, de una escuadra o el transportador. Para el inciso b) pueden usar el ángulo de 60º de la escuadra o el transportador. Respecto del inciso d), al jalar los vértices se forman rombos diferentes, debido a que cambia la medida de los ángulos.

Sugerencia didáctica. En las actividades 1 y 2 es posible que los alumnos piensen que para hacer el trazo necesitan un dato más (la altura o la base, respectivamente). Mientras los equipos resuelven, hágales ver que lo que deben trazar es un rectángulo que cumpla con la condición pedida y que con ello están resolviendo el problema planteado; se espera que los alumnos se den cuenta de que se pueden trazar muchos rectángulos diferentes, construyendo gradualmente la idea de que para trazar un rectángulo y para que éste quede definido, se requiere, en este caso, saber tanto la medida de la base como de la altura (esto podrán verlo en el ejercicio 3).

Propósito de la actividad. Los alumnos deberán percatarse de que existen ciertas condiciones que dan lugar al trazo de figuras diferentes, y que existen condiciones que permiten determinar a una figura de manera única. En el caso del romboide que se sugiere, los alumnos identificarán que la base y la altura no son datos suficientes para determinarlo, pero que si se da el valor de un ángulo interior, entonces es posible determinarlo de manera única. Sugerencia didáctica. En la confrontación de resultados procure que los alumnos distingan un caso del otro y que hagan explícitas cuáles son las condiciones para cada uno de ellos.

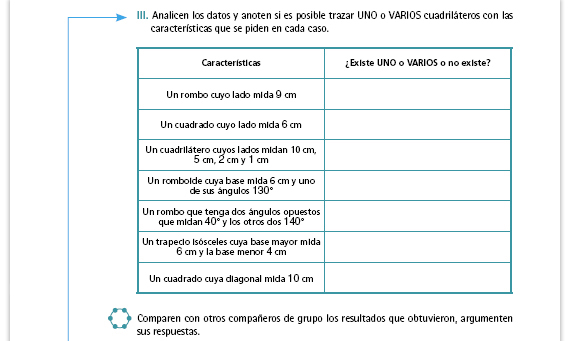
Propósito de la actividad.Todos los casos propuestos en la tabla permitirán a los alumnos establecer hipótesis y conjeturas acerca de la existencia y unicidad de las figuras, dadas ciertas condiciones, al mismo tiempo que tendrán que explotar posibles soluciones y validar o desechar sus hipótesis iniciales. En el caso del cuadrilátero del tercer renglón, si el tiempo se lo permite, invite a los alumnos a construirlo y a que argumenten por qué no es posible construirlo. La razón es que la suma de las longitudes de los tres lados más pequeños es menor que la longitud del lado más grande. Durante la puesta en común de las respuestas, invite a los alumnos a que ellos mismos se hagan cargo de la validación y defiendan sus respuestas, o que reconozcan cuando algún compañero les demuestre que están equivocados. Estas habilidades y actitudes son tan importantes como el contenido que se pretende que ellos construyan.

Características	¿Existe UNO o VARIOS o no existe?
Un rombo cuyo lado mida 9 cm	Varios (Pueden variar los ángulos)
Un cuadrado cuyo lado mida 6 cm	Uno (La medida de los ángulos es de 90º).
Un cuadrilátero cuyos lados midan 10 cm, 5 cm, 2 cmy 1 cm	No existe (La medida del lado mayor no debe exceder la suma de los otros tres).
Un romboide cuya base mida 6 cm y uno de sus ángulos 130º	Varios (EL otro lado puede tener cualquier longitud).
Un rombo que tenga dos ángulos opuestos que midan 40º y los otros 140º	Varios Puede variar la medida de los lados).
Un trapecio isósceles cuya base mayor mida 6 cm y la base menor 4 cm	Varios (Puede variar la altura).
Un cuadrado cuya diagonal mida 10 cm	Uno (Es un cuadrado de lado raíz cuadrada de 50).

Sugerencia didáctica. Para cerrar la sesión, además de comentar lo enunciado puede invitar a los alumnos a que ilustren casos en que las condiciones pedidas no pueden cumplirse para trazar un cuadrilátero, casos en que se cumplen pero hay varias soluciones posibles, y casos en que el cuadrilátero queda determinado de manera única. Integrar al portafolios. Solicite a los alumnos que realicen el siguiente ejercicio: a) Proponer las medidas para trazar un cuadrilátero (el que cada alumno elija), de tal manera que sea posible trazar varios cuadriláteros de distinto tamaño y forma. Trazar dos cuadriláteros. b) Proponer las medidas para trazar el cuadrilátero que eligieron anteriormente, de tal manera que todos los cuadriláteros que se tracen con esas medidas sean del mismo tamaño y forma. Trazar un cuadrilátero. Si los alumnos muestran dificultades para establecer cuáles son las características que cumplen con las condiciones anteriores, revise nuevamente con ellos las actividades I y II del apartado Manos a la obra y la información del apartado A lo que llegamos.

Propósito del video. Plantear y solucionar algunos problemas de trazo de triángulos y cuadriláteros con solución única o varias soluciones diferentes.