Propósito de la sesión. Aplicar conocimientos sobre el cálculo de áreas y perímetros en la resolución de problemas. Organización del grupo. Se recomienda que los alumnos resuelvan todos los problemas organizados en parejas y que al final se comparen los resultados. Si lo considera conveniente, pueden resolver un problema e inmediatamente comparar los resultados. Materiales. Instrumentos geométricos y calculadora.

Eje

Forma, espacio y medida.

Tema

Medida.

Antecedentes

Desde primer grado de primaria los alumnos han tenido contacto con las magnitudes de área y longitud. Se espera que en este grado los alumnos ya sepan calcular áreas utilizando diferentes procedimientos; particularmente en la secuencia 14 tuvieron la oportunidad de justificar algunas fórmulas para calcular áreas y perímetros. En esta ocasión continuarán resolviendo problemas de cálculo de áreas vinculando ese conocimiento con otros, por ejemplo, con las ecuaciones y con las situaciones de variación proporcional.

Propósitos de la secuencia Resolver problemas que impliquen calcular el perímetro y el área de triángulos, romboides y trapecios y establecer relaciones entre los elementos que se utilizan para calcular el área de cada una de estas figuras. Realizar conversiones de medidas de superficie.
Sesión	Título y propósitos de la sesión	Recursos
1	Problemas de aplicación Aplicar conocimientos sobre el cálculo de áreas y perímetros en la resolución de problemas.
2	Relaciones importantes Resolver problemas de áreas en los que se debe plantear una ecuación o identificar relaciones de variación proporcional.
3	Medidas de superficie Resolver problemas que implican conversiones de unidades de superficie.	Video "Medidas de superficie"

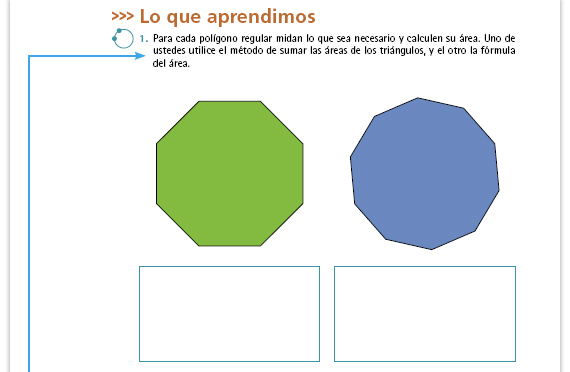
Propósito de la actividad. Que los alumnos decidan qué medidas deben tomar para calcular el área de una figura determinada. Posibles dificultades. Es probable que no puedan hacer mediciones exactas y, por lo tanto, que los resultados sean distintos. Proponga que utilicen aproximaciones. Esta es una oportunidad para reflexionar sobre la dificultad de obtener medidas exactas, así como sobre la necesidad de establecer un margen de error aceptable. Sugerencia didáctica. Pueden revisar la secuencia 14 con el fin de recordar la fórmula para calcular el área de un polígono regular. Es importante que los alumnos decidan qué es lo que tienen medir para calcular el área de cierta figura, si usted les da todos los datos para que sólo haga las operaciones, la situación se reduce a cálculos aritméticos. Mientras resuelven, identifique dificultades que usted pueda retomar en la comparación de resultados. Por ejemplo, en los alumnos que apliquen la fórmula usted puede observar cómo determinan la medida del apotema.

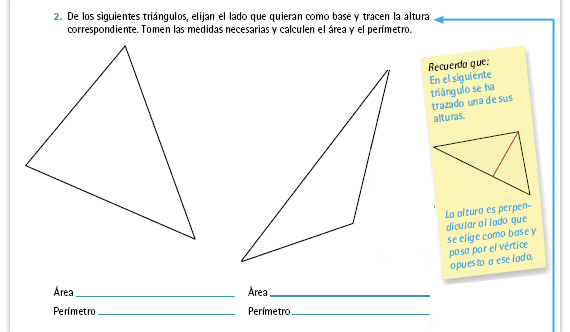
Sugerencia didáctica. Un aspecto que es interesante observar en los procedimientos de los alumnos es cómo determinan la altura de cada uno de los triángulos; particularmente para el caso del segundo triángulo, si eligen como base el lado de menor longitud necesitarán prolongar este lado para poder trazar la perpendicular que va al vértice opuesto. Sin embargo, es probable que pocos alumnos hagan esto, por lo que usted puede aprovechar la comparación de resultados para plantear esta situación. También es pertinente que los alumnos reflexionen en torno de que aun cuando se hayan considerado distintas alturas en cada uno de los triángulos, el área debe ser la misma.

Sugerencia didáctica. Puede dejar este ejercicio como tarea. Los alumnos tienen dos posibilidades para trazar un triángulo distinto pero con la misma área que el de la lección: pueden utilizar las mismas medidas de la base y la altura, pero deben "mover" la altura (que pase por la mitad de la base, por ejemplo) para que el triángulo resulte distinto al de la lección. Otra forma es variar las medidas de la base y de la altura de tal manera que obtengan la misma área.

Posibles procedimientos. Este problema es de mayor complejidad que los anteriores no sólo porque se trata de una figura irregular y los alumnos tendrán que decidir cómo hacer particiones, sino también porque es una figura hecha a escala. Una forma de resolverlo es dividir el terreno en figuras conocidas, (pueden ser triángulos, rectángulos y romboides), calcular el área de cada una de ellas considerando desde un inicio la escala (1 cm en el dibujo equivale a 200 cm) y después sumar las áreas para obtener el área total. Si los alumnos no consideran la escala desde un inicio, pueden obtener el área del dibujo y aplicar después la escala, aunque esto es más complejo: el área obtenida en el dibujo es aproximadamente de 24 cm2 , y 1 cm en el dibujo equivale a 200 cm, entonces 1 cm2 equivale a 40 000 cm2. El área es de 96 000 cm2. Seguramente las diferencias en las medidas serán más notorias en este caso, pero siempre dentro de un margen de error en el que los alumnos tendrán que decidir si tales diferencias se deben a las imprecisiones al medir o a un cálculo erróneo.

Sugerencia didáctica. Si los alumnos no recuerdan la fórmula, recomiéndeles que consulten la secuencia 14. Respuesta. La fórmula es A = 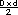, y el resultado es 1 750 cm2.

Integrar al portafolios. El reto que tienen los alumnos con este problema es que aun cuando se dan las medidas, deberán decidir cuáles de ellas deben tomar en cuenta para calcular lo que se cobrará en cada caso (el costo de los cimientos, de los castillos y del tabique). Tal vez las dificultades que se presenten tengan que ver precisamente con no poder decidir qué medidas considerar, por ello es importante que durante la comparación de resultados dedique mayor tiempo para analizar cuáles son la medidas que los alumnos deben tomar en cuenta y por qué. Respuestas. -Costo de los cimientos: se requiere calcular el perímetro del terreno, que es de 36 m, y se multiplica por el costo de cada metro: 36 × 200 = $7 200. -Costo de los castillos: son 9 castillos y cada castillo tiene 3 m de altura, es decir que son 27 metros en total. 27 × 80 = $2 160. -Costo de la barda: quitando el hueco para el zaguán, la barda tiene un perímetro de 33 m. Considerando los 3 m de altura: 33 m × 3 m de altura son 99 m2 de barda: 99 × 50 = $4 950. -El costo total de la mano de obra es de $14 310.

Sugerencia didáctica. Para hacer más ágil el momento de la confrontación, centre la atención en la medición y en los procedimientos para calcular el área y/o perímetro de cada una de las figuras, no en los cálculos. Es decir, si se tienen que hacer cálculos pida sólo los resultados al equipo, o bien, pida a alguien que traiga calculadora que verifique los cálculos; recuerde que el propósito de esta secuencia no es ejercitar las operaciones.