
|

|

|
 |
 |

| Propósito de la sesión. Resolver
problemas de áreas en los que se debe
plantear una ecuación o identificar
relaciones de variación proporcional.
Organización del grupo. Se sugiere que los alumnos resuelvan en equipo todas las actividades de la sesión. |

| Propósito de las actividades. Que los
alumnos recurran a otros conocimientos
que tienen vínculos con el cálculo de
áreas y perímetros; en los primeros
cuatro problemas ponen en juego
el planteamiento y la resolución de
ecuaciones, y en los siguientes problemas
se explora la noción de variación
proporcional vinculándola con problemas
de áreas y perímetros.
Sugerencia didáctica. Comente a los alumnos que los primeros cuatro problemas pueden resolverse por medio de las ecuaciones que ya estudiaron en la secuencia 18, mencione que hay otras formas de resolverlos pero que en este momento se trata de que apliquen el planteamiento y la resolución de ecuaciones en este tipo de problemas. Invítelos a que verifiquen cada una de las ecuaciones que resuelvan. En un primer momento permita que los alumnos determinen cuál es la incógnita en cada problema. Si nota que algún equipo tiene dificultades, apóyelos con las siguientes preguntas:
|

| Respuesta.
Considerando que la
servilleta tiene 4 lados iguales y el total
del perímetro es de 1.60 m, una forma
de plantear y resolver la ecuación es la
siguiente:
4x = 1.60 x = 1.60 ÷ 4 x = 0.40 La servilleta mide 40 cm por lado. |

| Respuesta.
El área del rectángulo se
obtiene multiplicando largo por ancho.
Una forma de plantear y resolver la
ecuación es la siguiente:
1.5x = 40 x = 40 ÷ 1.5 x = 26.6666666... Si se redondea la cantidad, el largo de la tela es de 26.67 cm. |

| Respuesta. Para calcular el área del
rectángulo se necesita encontrar primero la
medida del ancho. Una forma de resolver es la
siguiente:
El largo mide x. El ancho mide x - 6. El perímetro es de 28 cm. El perímetro se calcula de la siguiente manera: 2 veces el largo + 2 veces el ancho; una manera de plantear y resolver la ecuación es: 2x + 2 (x - 6) = 28 2x + 2 x - 12 = 28 4x - 12 = 28 4x = 28 + 12 4x = 40 x = 40 ÷ 4 x = 10 El largo mide 10 cm y el ancho mide 4 cm. El área es de 40 cm2. |
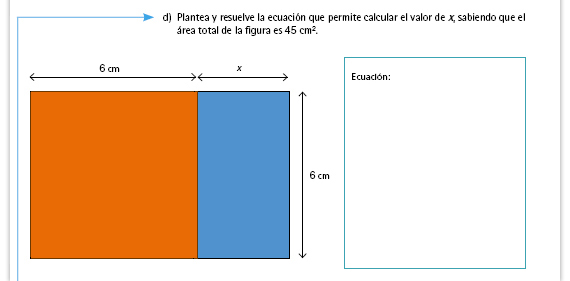
Incorporar al portafolios. Las siguientes son
algunas formas de resolver el problema:
|

Sugerencia didáctica. Los alumnos han
tenido varias experiencias con problemas
de proporcionalidad en distintos contextos,
ahora se trata de que vinculen esa experiencia
con problemas de área y perímetros. Una
vez que hayan resuelto la primera tabla,
usted puede hacer un breve recordatorio
sobre las características de una relación de
proporcionalidad directa, apoyándose en las
siguientes preguntas:
|

| Respuesta. Sí es una relación de proporcionalidad. La constante de proporcionalidad es 4 porque todas las medidas de la primera columna se multiplican por 4 para obtener las medidas de la segunda columna. |
| Respuesta. Sí es una relación de proporcionalidad. La constante de proporcionalidad es 4 porque todas las medidas de la primera columna se multiplican por 4 para obtener las medidas de la segunda columna. |

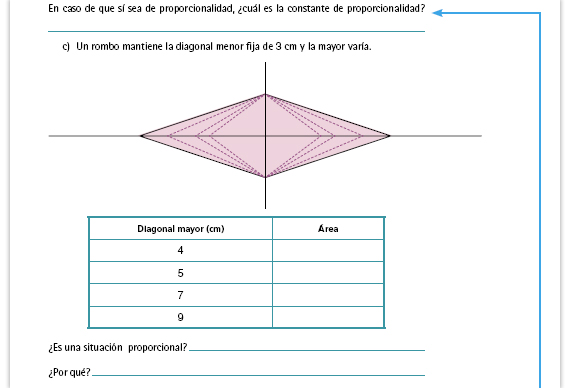
Respuesta. Si es una relacion de
proporcionalidad. La constante de
proporcionalidad esta compuesta por
dos operaciones: multiplicar por 3 y
dividir entre 2, que es lo mismo que
multiplicar por 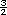 o por 1.5. Todas
las medidas de la primera columna
se multiplican por o por 1.5. Todas
las medidas de la primera columna
se multiplican por 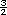 o por 1.5 para
obtener las medidas de la segunda
columna. o por 1.5 para
obtener las medidas de la segunda
columna. |
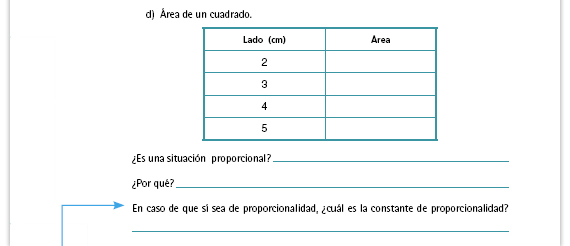
| Respuesta. No es una situación de proporcionalidad, por lo tanto no hay constante de proporcionalidad: cada medida de la primera columna se multiplica por un número distinto para obtener las medidas de la segunda columna. |