Propósito de la sesión. Resolver problemas que implican conversiones de unidades de superficie. Organización del grupo. Se sugiere que los alumnos resuelvan la sesión organizados en parejas.

Posibles procedimientos del Consideremos lo siguiente. Algunas formas de calcular el área, son: 1.. Cuadricular el mapa. 2.. Hacer un polígono que se ajuste lo más posible al contorno del mapa y dividir el polígono en figuras conocidas; calcular el área de cada figura y después sumarlas. 3.. Hacer un rectángulo que cubra todo el mapa, calcular el área del rectángulo y después restarle el área de las figuras que quedaron dentro y que no corresponden al mapa. El área que obtengan en cm2 debe multiplicarse por 775 0002, esto es: partiendo de que cada cm equivale en la realidad a 775 000 cm, que es igual a 7 750 m o 7.75 km; por lo tanto, cada cm2 equivale a 600 625 000 000 cm2, que es igual a 60 062 500 m2 o 60.0625 km2. Hacer esta conversión desde el inicio facilita todo el procedimiento, porque una vez que tienen el área en cm2, la multiplican por 600 625 000 000 cm2 o por cualquiera de las equivalencias anteriores, aunque la más conveniente es la de km2, pues si lo hacen con cm2 las cantidades son más difíciles de operar por el número de cifras. Posibles errores. Este problema es complejo para los alumnos porque involucra una figura a escala; no obstante, cuentan con conocimientos que les permitirán resolverlo (en el problema 3 de la sesión 1 de esta secuencia resolvieron un problema de escala). La dificultad está en la conversión que hagan de la escala 1:775 000 a cm2. En general, las conversiones de unidades de superficie es un tema difícil para los alumnos porque transfieren las reglas de cambio de las longitudes a las de la superficie. Por ejemplo, si un metro equivale a 10 decímetros, los estudiantes podrían creer que 1 metro cuadrado también equivale a 10 decímetros cuadrados. En este caso, la escala se refiere a longitudes y no a superficies, por lo que un error probable es que calculen el área en cm2 y crean que hay que multiplicar este resultado por 775 000 para obtener la medida real.

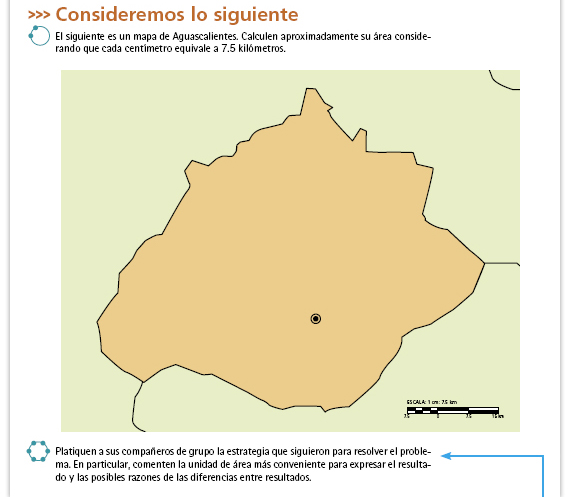
Sugerencia didáctica. En los intercambios de los alumnos procure dar mayor énfasis a las unidades de superficie que utilizan para expresar el resultado, pídales que las comparen para ver si son equivalentes; esto dará lugar a conversiones de medidas de superficie. En caso de que no haya acuerdos o que no todas las parejas logren validar sus resultados, sugiérales que continúen con la lección, pues en ella podrán encontrar elementos que les permitirán regresar al problema inicial y revisar nuevamente sus respuestas.

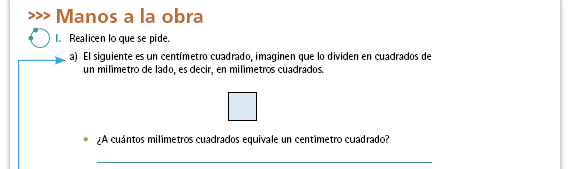
Propósito de la actividad. Para que los alumnos logren construir la idea de que 1 cm2 NO equivale a 10 mm2 sino a 100 mm2, así como 1 dm2 equivale a 100 cm2 o a 10 000 mm2, es importante que cuenten con un referente concreto o gráfico en el que puedan visualizar estas equivalencias. Por ello se les presentan los dibujos de un centímetro cuadrado y de un decímetro cuadrado, y se les pide que los dividan en otras unidades de superficie para que visualicen la equivalencia correspondiente. Sugerencia didáctica. Si lo considera necesario, puede pedir a los alumnos que construyan con papel el cm2 y el dm2 y que superpongan el primero en el segundo las veces que sea necesario para que vean "cuántas veces cabe" uno en el otro, es decir a cuántos cm2 equivale un dm2.

Propósito de la actividad. Es muy común que aun cuando los alumnos hablan del metro cuadrado no tengan una idea precisa del tamaño de esta unidad de medida, por ello es importante que construyan un metro cuadrado para que tengan un referente de su tamaño y logren hacer estimaciones sobre resultados correctos o incorrectos. Respuestas. -Un m2 equivale a 100 dm2. (10 dm por lado). -Un m2 equivale a 10 000 cm2. (100 cm por lado). -Un m2 equivale a 1 000 000 mm2. (1 000 mm por lado).

Sugerencia didáctica. Así como es importante que los alumnos puedan estimar el tamaño de un metro cuadrado, también es necesario que lo hagan con una hectárea (ha). Procure que efectivamente se haga la medición del patio de la escuela, pues esta actividad les ayudará a estimar, a partir de un referente cercano, cuál es el tamaño de la hectárea. Además de calcular cuánto le falta al patio para ser una hectárea, pueden también calcular cuántos patios como el de su escuela se necesitan para tener esa superficie. Respuesta. Una hectárea equivale a 10 000 m2 (100 m por lado).

Sugerencia didáctica. Tener un referente concreto del tamaño de un kilómetro cuadrado es más difícil; no obstante, los alumnos podrían calcular cuántos patios como el de la escuela se requieren para formar un kilómetro cuadrado. También podrían partir de algún referente (como la distancia de la escuela a algún punto de la comunidad) que les permita formarse una idea de un kilómetro lineal e imaginarse un cuadrado que mida un km por lado. Respuesta. Un km2 equivale a 100 hectáreas. km2 son 1 000 000 m2. 1 hectárea son 10 000 m2. Entonces, en un km2 caben 100 hectáreas.

Pida a una pareja de alumnos que elaboren un cartel con esta información para que se cuelgue en alguna parte del salón. Todos los alumnos pueden copiar en el cuaderno esa información e ilustrar algunas medidas, como el cm2 y el dm2. Asimismo, pueden agregar a sus notas las comparaciones que hicieron del patio de la escuela con algunas medidas de superficie (ha y km2). Si lo considera necesario, puede plantear algunas conversiones como las que se sugieren en seguida, para que los alumnos las resuelvan en el cuaderno: Completa la tabla haciendo las conversiones necesarias:

Estados de la República Mexicana	Superficie en km2	Superficie en ha
Sonora	184 934
Morelos		49.41
Oaxaca	95 364
Distrito Federal		14.99

Propósitos del video. Conocer diferentes unidades para medir áreas y visualizar sus equivalencias.